北师大版八下1.2.1 直角三角形(1) 课件
文档属性
| 名称 | 北师大版八下1.2.1 直角三角形(1) 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 17:50:16 | ||
图片预览








文档简介
(共29张PPT)
第一章 三角形的证明
1.2.1 直角三角形(1)
北师大版 数学 八年级 下册
学习目标
1 能够证明直角三角形的性质定理和判定定理,进一步熟悉证明的基本步骤和书写格式,体会证明的必要性;
2 体验数学活动中的探索与创造,感受数学的严谨性.
情景导入
直角三角形的定义:
有一个角是直角的三角形是直角三角形
在前面我们已经学习了等腰三角形,你知道等腰三角形有哪些性质?怎样判定一个三角形是等腰三角形呢?
今天我们要学习的直角三角形作为一种特殊的三角形,是如何定义的呢?除了具有一般三角形的性质外,它还具有哪些特殊性质呢?
C
A
B
情景导入
直角三角形有哪些性质?怎样判定一个三角形是直角三角形呢?
性质 判定
定理1:
直角三角形的两个锐角互余
定理2:
有两个角互余的三角形是直角三角形;
定理3:
(勾股定理)
直角三角形的两条直角边的平方和等于斜边的平方。
定理4:
如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
核心知识点一:
直角三角形的性质与判定
你能证明这两个结论吗?
想一想:
(1) 直角三角形的两个锐角有怎样的关系?为什么?
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为 什么?
探索新知
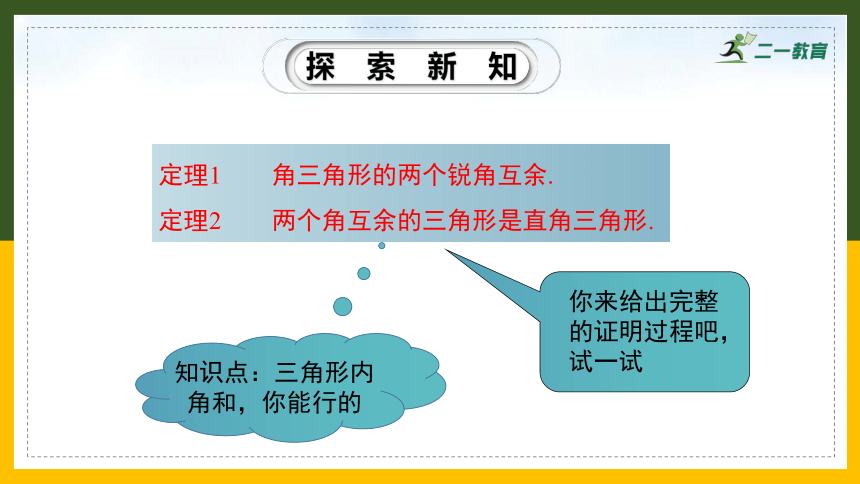
定理1 角三角形的两个锐角互余.
定理2 两个角互余的三角形是直角三角形.
知识点:三角形内角和,你能行的
你来给出完整的证明过程吧,试一试
探索新知
证明一个命题的一般步骤:
1.弄清楚条件(直角三角形)和结论(两个锐角互余);
2.根据题意画出相应的图形;
3.由条件和结论,写出已知和求证;
4.分析证明思路,写出证明过程。
探索新知
已知:如图,在Rt△ABC,∠C=90°
求证:∠A+∠B=90°
证明:在△ABC中,
∠A+∠B+∠C=180°
∵∠C=90°
∴∠A+∠B=180°-∠C
=180°-90°=90°
定理1:直角三角形两锐角互余
几何语言:
∵在Rt△ABC中,∠C=90°
∴∠A+∠B=90°
探索新知
已知:如图,在△ABC中,∠A+∠B=90°
求证:△ABC是直角三角形。
证明:在△ABC中,
∠A+∠B+∠C=180°
又∵∠A+∠B=90°
∴∠C=180°-(∠A+∠B)
=180°-90°=90°
∴这个三角形是直角三角形
定理2:有两锐角互余的三角形是直角三角形
几何语言:
∵在Rt△ABC中,∠A+∠B=90°
∴△ABC是直角三角形
探索新知
例1:如图,在△ABC中,∠C=70°,∠B=30°,AD⊥BC于点D,AE为∠BAC的平分线,求∠DAE的度数.
探索新知
解:由题意可知,
∠BAC=180°-∠B-∠C=80°.
∵AE为∠BAC的平分线,
∴∠CAE=∠BAE= ∠BAC=40°.
∵AD⊥BC,∴∠ADC=90°.
∴∠CAD=90°-∠C=90°-70°=20°.
∴∠DAE=∠CAE-∠CAD=40°-20°=20°.
探索新知
核心知识点二:
勾股定理与逆定理
你还记得勾股定理的内容吗?
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
a
c
b
如果将勾股定理反过来,怎么叙述呢?
即a2+b2=c2.
探索新知
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
我们曾用度量的办法得出这个结论.
思考:这个命题是真命题吗?为什么?
是否还有其他方法?
探索新知
已知:如图,在△ABC中,AC2+AB2=BC2.
求证:△ABC是直角三角形.
证明:如图,作 Rt△A′B′C′,
使∠A′=90°,A′B′=AB,A′C′=AC,
则 A′B′2+A′C′2=B′C′2(勾股定理).
∵ AB2+AC2=BC2,∴ BC2=B′C′2.
∴ BC=B′C′. ∴△ABC≌△A′B′C′(SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
因此,△ABC 是直角三角形.
探索新知
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
几何语言:
∵a2+b2=c2.
∴△ABC是直角三角形
a
c
b
探索新知
例2 :已知:在△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm.
求证:AB=AC.
探索新知
解:如图,因为AD是BC边上的中线,
所以BD= BC= ×10=5(cm).
在△ABD中,∵AB=13 cm,AD=12 cm,BD=5 cm,
∴AB2=AD2+BD2.
∴△ABD为直角三角形.所以AD⊥BC.
在Rt△ADC中,AC= =13(cm),
所以AB=AC.
探索新知
核心知识点三:
互逆命题与互逆定理
定理4: 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
定理3:直角三角形两条直角边的平方和等于
斜边的平方。
定理1:直角三角形的两个锐角互余.
定理2:有两个锐角互余的三角形是直角三角形.
观察:这两组定理,它们的条件和结论之间有怎样的关系?
如果A,那么B.
如果B,那么A.
条件和结论互换
探索新知
如果小明发烧,那么他一定患了肺炎。
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等。
如果小明患了肺炎,那么他一定会发烧;
观察以下三组命题,每组中两个命题的条件和结论也有类似这样的关系吗?
在两个命题中,如果一个命题的______和______分别是另一个命题的______和_______,那么这两个命题称为___________,其中一个命题称为另一个命题的______________。
条件
结论
结论
条件
互逆命题
逆命题
如果两个角是对顶角,那么他们相等;
如果两个角相等,那么它们是对顶角。
探索新知
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为_____________,其中一个定理称为另一个定理的________。
一个命题是真命题,它的逆命题却__________是真命题。
不一定
互逆定理
逆定理
假
真
真
真
假
假
以下三组命题,都是真命题吗?
如果小明发烧,那么他一定患了肺炎。
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等。
如果小明患了肺炎,那么他一定会发烧;
如果两个角是对顶角,那么他们相等;
如果两个角相等,那么它们是对顶角。
探索新知
当堂检测
1.一直角三角形的两边长分别为3和4,则第三边的长为( ) .
D
A.5 B. C. D.5或
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三
角形的是( ) .
B
A. , , B.1, ,
C.6,7,8 D.2,3,4
当堂检测
3.在 中, 所对的边为 , 所对的边为 , 所对的边
为 ,下列选项中不能判定 为直角三角形的是( ) .
D
A. B.
C. , , D.
4.在 中, , ,则 ( ) .
D
A.8 B.16或64 C.4 D.4或16
当堂检测
5.满足下列条件的 是直角三角形的是( ) .
D
A. B.
C. D. , ,
6.三角形的三边长分别为 , , ,则下面四种情况,不能判断此
三角形为直角三角形的是( ) .
D
A. , , B. , ,
C. , , D. , ,
当堂检测
7.在△ABC 中,三边长a,b,c 满足(a+c )(a-c )=b 2,则
△ABC 的形状是( ).
A.以a 为斜边长的直角三角形
B.以b 为斜边长的直角三角形
C.以c 为斜边长的直角三角形
D.不是直角三角形
A
当堂检测
8.如图,在 中, ,过点 作 , 平分 ,若 ,则 的度数为_____.
当堂检测
9.如图,在△ABC中,∠B=30°,∠C=62°,AE平分∠BAC.
(1)求∠BAE的度数;
(1)解:∵∠B=30°,∠C=62°,
∴∠BAC=180°-∠B-∠C=88°.
∵AE平分∠BAC,
∴∠BAE=∠BAC=×88°=44°.
当堂检测
(2)若AD⊥BC于点D,∠ADF=74°,求证:△ADF是直角三角形.
(2)证明:∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B=60°.
由(1)知∠BAE=44°,
∴∠EAD=∠BAD-∠BAE=16°,
∴∠ADF+∠EAD=90°,
∴∠AFD=90°,
∴△ADF是直角三角形.
直角三角形
角的性质
边的性质
勾股定理:直角三角形两条直角边的平方和等于斜边的平方;
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
定理1:直角三角形的两个锐角互余;
定理2:有两个角互余的三角形是直角三角形
互逆定理(均真)
感谢收看
第一章 三角形的证明
1.2.1 直角三角形(1)
北师大版 数学 八年级 下册
学习目标
1 能够证明直角三角形的性质定理和判定定理,进一步熟悉证明的基本步骤和书写格式,体会证明的必要性;
2 体验数学活动中的探索与创造,感受数学的严谨性.
情景导入
直角三角形的定义:
有一个角是直角的三角形是直角三角形
在前面我们已经学习了等腰三角形,你知道等腰三角形有哪些性质?怎样判定一个三角形是等腰三角形呢?
今天我们要学习的直角三角形作为一种特殊的三角形,是如何定义的呢?除了具有一般三角形的性质外,它还具有哪些特殊性质呢?
C
A
B
情景导入
直角三角形有哪些性质?怎样判定一个三角形是直角三角形呢?
性质 判定
定理1:
直角三角形的两个锐角互余
定理2:
有两个角互余的三角形是直角三角形;
定理3:
(勾股定理)
直角三角形的两条直角边的平方和等于斜边的平方。
定理4:
如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
核心知识点一:
直角三角形的性质与判定
你能证明这两个结论吗?
想一想:
(1) 直角三角形的两个锐角有怎样的关系?为什么?
如果一个三角形有两个角互余,那么这个三角形
是直角三角形吗?为 什么?
探索新知
定理1 角三角形的两个锐角互余.
定理2 两个角互余的三角形是直角三角形.
知识点:三角形内角和,你能行的
你来给出完整的证明过程吧,试一试
探索新知
证明一个命题的一般步骤:
1.弄清楚条件(直角三角形)和结论(两个锐角互余);
2.根据题意画出相应的图形;
3.由条件和结论,写出已知和求证;
4.分析证明思路,写出证明过程。
探索新知
已知:如图,在Rt△ABC,∠C=90°
求证:∠A+∠B=90°
证明:在△ABC中,
∠A+∠B+∠C=180°
∵∠C=90°
∴∠A+∠B=180°-∠C
=180°-90°=90°
定理1:直角三角形两锐角互余
几何语言:
∵在Rt△ABC中,∠C=90°
∴∠A+∠B=90°
探索新知
已知:如图,在△ABC中,∠A+∠B=90°
求证:△ABC是直角三角形。
证明:在△ABC中,
∠A+∠B+∠C=180°
又∵∠A+∠B=90°
∴∠C=180°-(∠A+∠B)
=180°-90°=90°
∴这个三角形是直角三角形
定理2:有两锐角互余的三角形是直角三角形
几何语言:
∵在Rt△ABC中,∠A+∠B=90°
∴△ABC是直角三角形
探索新知
例1:如图,在△ABC中,∠C=70°,∠B=30°,AD⊥BC于点D,AE为∠BAC的平分线,求∠DAE的度数.
探索新知
解:由题意可知,
∠BAC=180°-∠B-∠C=80°.
∵AE为∠BAC的平分线,
∴∠CAE=∠BAE= ∠BAC=40°.
∵AD⊥BC,∴∠ADC=90°.
∴∠CAD=90°-∠C=90°-70°=20°.
∴∠DAE=∠CAE-∠CAD=40°-20°=20°.
探索新知
核心知识点二:
勾股定理与逆定理
你还记得勾股定理的内容吗?
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
a
c
b
如果将勾股定理反过来,怎么叙述呢?
即a2+b2=c2.
探索新知
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
我们曾用度量的办法得出这个结论.
思考:这个命题是真命题吗?为什么?
是否还有其他方法?
探索新知
已知:如图,在△ABC中,AC2+AB2=BC2.
求证:△ABC是直角三角形.
证明:如图,作 Rt△A′B′C′,
使∠A′=90°,A′B′=AB,A′C′=AC,
则 A′B′2+A′C′2=B′C′2(勾股定理).
∵ AB2+AC2=BC2,∴ BC2=B′C′2.
∴ BC=B′C′. ∴△ABC≌△A′B′C′(SSS).
∴ ∠A=∠A′=90°(全等三角形的对应角相等).
因此,△ABC 是直角三角形.
探索新知
定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
几何语言:
∵a2+b2=c2.
∴△ABC是直角三角形
a
c
b
探索新知
例2 :已知:在△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm.
求证:AB=AC.
探索新知
解:如图,因为AD是BC边上的中线,
所以BD= BC= ×10=5(cm).
在△ABD中,∵AB=13 cm,AD=12 cm,BD=5 cm,
∴AB2=AD2+BD2.
∴△ABD为直角三角形.所以AD⊥BC.
在Rt△ADC中,AC= =13(cm),
所以AB=AC.
探索新知
核心知识点三:
互逆命题与互逆定理
定理4: 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
定理3:直角三角形两条直角边的平方和等于
斜边的平方。
定理1:直角三角形的两个锐角互余.
定理2:有两个锐角互余的三角形是直角三角形.
观察:这两组定理,它们的条件和结论之间有怎样的关系?
如果A,那么B.
如果B,那么A.
条件和结论互换
探索新知
如果小明发烧,那么他一定患了肺炎。
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等。
如果小明患了肺炎,那么他一定会发烧;
观察以下三组命题,每组中两个命题的条件和结论也有类似这样的关系吗?
在两个命题中,如果一个命题的______和______分别是另一个命题的______和_______,那么这两个命题称为___________,其中一个命题称为另一个命题的______________。
条件
结论
结论
条件
互逆命题
逆命题
如果两个角是对顶角,那么他们相等;
如果两个角相等,那么它们是对顶角。
探索新知
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为_____________,其中一个定理称为另一个定理的________。
一个命题是真命题,它的逆命题却__________是真命题。
不一定
互逆定理
逆定理
假
真
真
真
假
假
以下三组命题,都是真命题吗?
如果小明发烧,那么他一定患了肺炎。
一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等。
如果小明患了肺炎,那么他一定会发烧;
如果两个角是对顶角,那么他们相等;
如果两个角相等,那么它们是对顶角。
探索新知
当堂检测
1.一直角三角形的两边长分别为3和4,则第三边的长为( ) .
D
A.5 B. C. D.5或
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三
角形的是( ) .
B
A. , , B.1, ,
C.6,7,8 D.2,3,4
当堂检测
3.在 中, 所对的边为 , 所对的边为 , 所对的边
为 ,下列选项中不能判定 为直角三角形的是( ) .
D
A. B.
C. , , D.
4.在 中, , ,则 ( ) .
D
A.8 B.16或64 C.4 D.4或16
当堂检测
5.满足下列条件的 是直角三角形的是( ) .
D
A. B.
C. D. , ,
6.三角形的三边长分别为 , , ,则下面四种情况,不能判断此
三角形为直角三角形的是( ) .
D
A. , , B. , ,
C. , , D. , ,
当堂检测
7.在△ABC 中,三边长a,b,c 满足(a+c )(a-c )=b 2,则
△ABC 的形状是( ).
A.以a 为斜边长的直角三角形
B.以b 为斜边长的直角三角形
C.以c 为斜边长的直角三角形
D.不是直角三角形
A
当堂检测
8.如图,在 中, ,过点 作 , 平分 ,若 ,则 的度数为_____.
当堂检测
9.如图,在△ABC中,∠B=30°,∠C=62°,AE平分∠BAC.
(1)求∠BAE的度数;
(1)解:∵∠B=30°,∠C=62°,
∴∠BAC=180°-∠B-∠C=88°.
∵AE平分∠BAC,
∴∠BAE=∠BAC=×88°=44°.
当堂检测
(2)若AD⊥BC于点D,∠ADF=74°,求证:△ADF是直角三角形.
(2)证明:∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°-∠B=60°.
由(1)知∠BAE=44°,
∴∠EAD=∠BAD-∠BAE=16°,
∴∠ADF+∠EAD=90°,
∴∠AFD=90°,
∴△ADF是直角三角形.
直角三角形
角的性质
边的性质
勾股定理:直角三角形两条直角边的平方和等于斜边的平方;
逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
定理1:直角三角形的两个锐角互余;
定理2:有两个角互余的三角形是直角三角形
互逆定理(均真)
感谢收看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
