北师大版八下1.2.2直角三角形(2) 课件
文档属性
| 名称 | 北师大版八下1.2.2直角三角形(2) 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 17:50:16 | ||
图片预览






文档简介
(共25张PPT)
第一章 三角形的证明
1.2.2直角三角形(2)
北师大版 数学 八年级 下册
学习目标
1、能够证明直角三角形全等的“HL”判定定理;
2、能根据“HL”定理解决实际问题.
情景导入
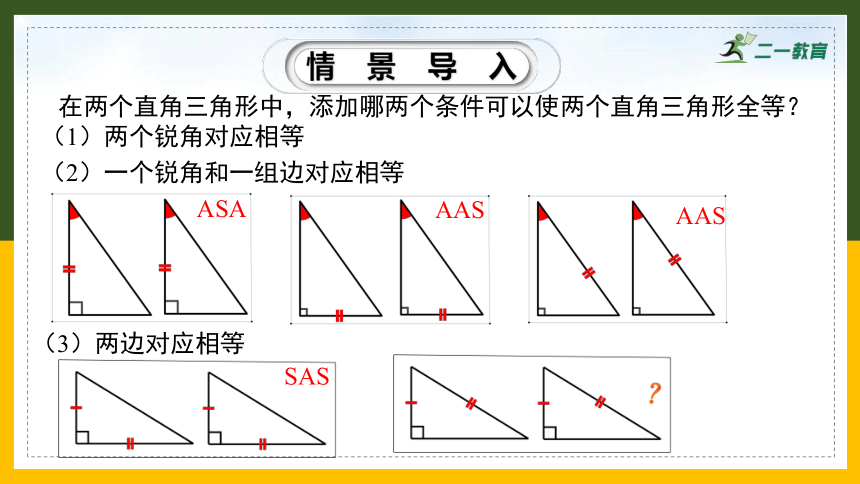
在两个直角三角形中,添加哪两个条件可以使两个直角三角形全等?
(1)两个锐角对应相等
(2)一个锐角和一组边对应相等
(3)两边对应相等
ASA
AAS
SAS
AAS
情景导入
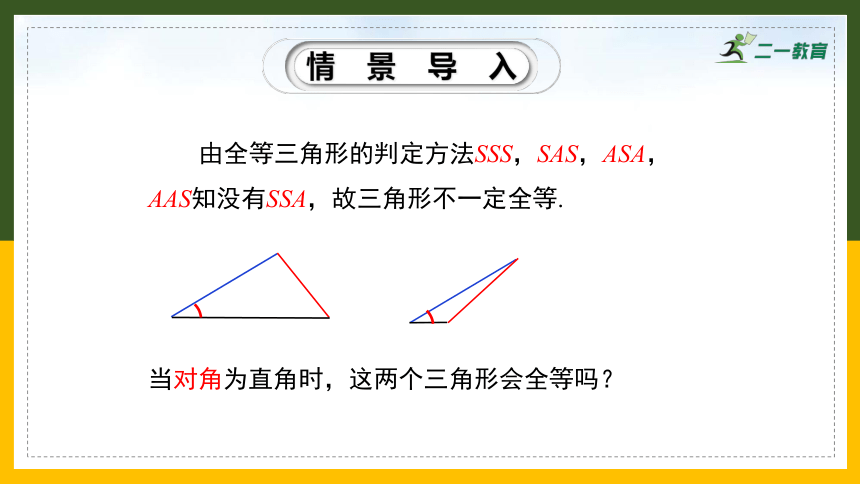
由全等三角形的判定方法SSS,SAS,ASA,AAS知没有SSA,故三角形不一定全等.
当对角为直角时,这两个三角形会全等吗?
核心知识点一:
直角三角形全等的判定(“斜边、直角边”定理)
动手操作,猜想结论
已知:线段ɑ、c(ɑ<c),直角α.
求作:Rt△ABC,使∠C=∠α,BC=ɑ,AB=c.
探索新知
(1)作∠MCN=∠α=90°.
M
C
N
M
探索新知
(2)在射线CM上截取CB=ɑ.
M
C
N
B
M
探索新知
(3)以点B为圆心,线段c的长为半径作弧,交射线CN于A.
M
C
N
B
M
A
探索新知
A
M
C
N
B
M
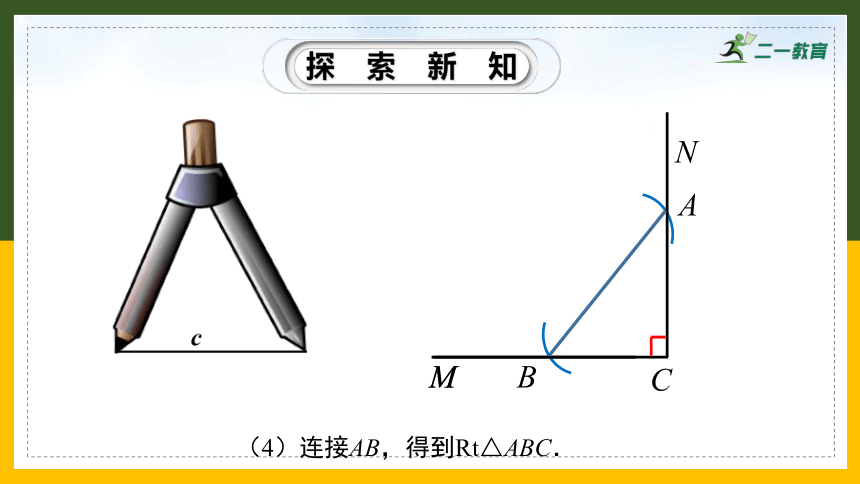
(4)连接AB,得到Rt△ABC.
探索新知
把作好的三角形剪下来,与同桌作的三角形对比,
两个三角形是否能够完全重合?
结论:斜边和一条直角边分别相等的两个直角三角形全等.
探索新知
已知:如图,在 △ABC与△A′B′C′中,∠C=∠C′=90°,AB=A′B′,
求证: △ABC≌△A′B′C′
A
B
C
A′
B′
C′
探索新知
A
B
C
A′
B′
C′
证明:在△ABC中,
∵∠C= 90°,
∴BC2= AB2-AC2 (勾股定理).
同理, B′C′ 2=A′B′2-A′C′ 2.
∵AB=A′B′, AC=A′C′,
∴BC=B′C′.
∴ △ABC≌△A′B′C′(SSS).
探索新知
归纳总结
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
A
B
C
A ′
B′
C ′
探索新知
例: 如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
探索新知
证明:在Rt△ABC和Rt△DEF中,
∴Rt△BAC≌Rt△EDF (HL).
∴∠B=∠DEF (全等三角形的对应角相等).
∵∠DEF+∠F=90°,(直角三角形的两锐角互余),
∴∠B+∠F=90°
BC=EF,
AC=DF ,
探索新知
当堂检测
1.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充的
条件是( ).
A.AC=AD或BC=BD
B.AC=AD且BC=BD
C.∠BAC=∠BAD
D.以上都不对
A
当堂检测
2.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF 相等,且这两个滑梯与地面夹角中∠ABC=32°,则∠DFE的度数是( ).
A.32°
B.62°
C.58°
D.68°
C
当堂检测
3.如图,在Rt△ABC 中,∠ACB=90°,AC=3,BC=4,BE 平分∠ABC,CD⊥AB 于D,BE 与CD 相交于F,则CF 的长是( ).
A.1
B.2
C.
D.
C
当堂检测
4.用三角尺可按下面方法画角的平分线.如图,在∠AOB两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,可得△POM≌△PON.则判定三角形全等的依据是( ).
A.SSS
B.SAS
C.ASA
D.HL
D
当堂检测
5.如图,△ABC中,∠C=90°,点D在BC上,且DE⊥AB于点E,AE=AC,若BC=4,DE=1.5,则BD= .
2.5
当堂检测
6.如图,已知AD,CE是△ABC的两条高线,AD=CE,∠CAD=25°,则∠OCD= °.
40
当堂检测
7.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB的延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(1)证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
当堂检测
(2)若∠CAE=30°,求∠ACF的度数.
(2)解:∵AB=CB,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°,
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=15°+45°=60°.
斜边和一条直角边对应相等的两个直角三角形全等.
“斜边、直角边”
在直角三角形中
内容
前提条件
在直角三角形中,只要有两边对应相等,则直角三角形全等
使用方法
感谢收看
第一章 三角形的证明
1.2.2直角三角形(2)
北师大版 数学 八年级 下册
学习目标
1、能够证明直角三角形全等的“HL”判定定理;
2、能根据“HL”定理解决实际问题.
情景导入
在两个直角三角形中,添加哪两个条件可以使两个直角三角形全等?
(1)两个锐角对应相等
(2)一个锐角和一组边对应相等
(3)两边对应相等
ASA
AAS
SAS
AAS
情景导入
由全等三角形的判定方法SSS,SAS,ASA,AAS知没有SSA,故三角形不一定全等.
当对角为直角时,这两个三角形会全等吗?
核心知识点一:
直角三角形全等的判定(“斜边、直角边”定理)
动手操作,猜想结论
已知:线段ɑ、c(ɑ<c),直角α.
求作:Rt△ABC,使∠C=∠α,BC=ɑ,AB=c.
探索新知
(1)作∠MCN=∠α=90°.
M
C
N
M
探索新知
(2)在射线CM上截取CB=ɑ.
M
C
N
B
M
探索新知
(3)以点B为圆心,线段c的长为半径作弧,交射线CN于A.
M
C
N
B
M
A
探索新知
A
M
C
N
B
M
(4)连接AB,得到Rt△ABC.
探索新知
把作好的三角形剪下来,与同桌作的三角形对比,
两个三角形是否能够完全重合?
结论:斜边和一条直角边分别相等的两个直角三角形全等.
探索新知
已知:如图,在 △ABC与△A′B′C′中,∠C=∠C′=90°,AB=A′B′,
求证: △ABC≌△A′B′C′
A
B
C
A′
B′
C′
探索新知
A
B
C
A′
B′
C′
证明:在△ABC中,
∵∠C= 90°,
∴BC2= AB2-AC2 (勾股定理).
同理, B′C′ 2=A′B′2-A′C′ 2.
∵AB=A′B′, AC=A′C′,
∴BC=B′C′.
∴ △ABC≌△A′B′C′(SSS).
探索新知
归纳总结
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”).
几何语言:
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
AB=A′B′,
BC=B′C′,
A
B
C
A ′
B′
C ′
探索新知
例: 如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
探索新知
证明:在Rt△ABC和Rt△DEF中,
∴Rt△BAC≌Rt△EDF (HL).
∴∠B=∠DEF (全等三角形的对应角相等).
∵∠DEF+∠F=90°,(直角三角形的两锐角互余),
∴∠B+∠F=90°
BC=EF,
AC=DF ,
探索新知
当堂检测
1.如图,若要用“HL”证明Rt△ABC≌Rt△ABD,则还需补充的
条件是( ).
A.AC=AD或BC=BD
B.AC=AD且BC=BD
C.∠BAC=∠BAD
D.以上都不对
A
当堂检测
2.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF 相等,且这两个滑梯与地面夹角中∠ABC=32°,则∠DFE的度数是( ).
A.32°
B.62°
C.58°
D.68°
C
当堂检测
3.如图,在Rt△ABC 中,∠ACB=90°,AC=3,BC=4,BE 平分∠ABC,CD⊥AB 于D,BE 与CD 相交于F,则CF 的长是( ).
A.1
B.2
C.
D.
C
当堂检测
4.用三角尺可按下面方法画角的平分线.如图,在∠AOB两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,可得△POM≌△PON.则判定三角形全等的依据是( ).
A.SSS
B.SAS
C.ASA
D.HL
D
当堂检测
5.如图,△ABC中,∠C=90°,点D在BC上,且DE⊥AB于点E,AE=AC,若BC=4,DE=1.5,则BD= .
2.5
当堂检测
6.如图,已知AD,CE是△ABC的两条高线,AD=CE,∠CAD=25°,则∠OCD= °.
40
当堂检测
7.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB的延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(1)证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
当堂检测
(2)若∠CAE=30°,求∠ACF的度数.
(2)解:∵AB=CB,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°,
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=15°+45°=60°.
斜边和一条直角边对应相等的两个直角三角形全等.
“斜边、直角边”
在直角三角形中
内容
前提条件
在直角三角形中,只要有两边对应相等,则直角三角形全等
使用方法
感谢收看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
