第二单元 比例 基础卷(含答案) —2024-2025学年北师大版六年级数学下册
文档属性
| 名称 | 第二单元 比例 基础卷(含答案) —2024-2025学年北师大版六年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 431.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 22:44:30 | ||
图片预览




文档简介
第二单元 比例 基础卷
考试范围:六下第二单元 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、细心填空。(24分)
1.一个数与3、6、9正好可以组成比例,那么这个数可能 。(不止一种情况,请写完整哟。)
2.如果×a=b×(a、b均不为0),则 a:b= ,a比b多 %。
3.在比例里,两个外项互为倒数,其中一个内项是0.25,另一个内项是 。
4.有3,5,6三个数,再添上一个数 可以组成比例,组成的比例是 。
5. 热干面是武汉市的一种特色小吃,妈妈网购了5袋热干面共花了18.5元,总价与数量最简单的整数比是 ,比值是 ,这个比值表示 。
6.在比例尺是1:10000的地图上,小明家到学校8厘米,如果小明每分钟走50米,他从家到学校要走 分钟。
7.甲、乙两地距高大约是120000千米,在比例尺是1:500000000的地图上, 长是 厘米。
8.实际距离240千米,画在比例尺是1:8000000的地图上,应画 厘米。
9.一幅地图的比例尺是1:4000000,把它改成线段比例尺是 ,已知AB两地的实际距离是240千米,在这幅地图上应画 厘米。
10.陕西牛背梁自然保护区被誉为物种的“天然基因库”,保护区内两栖爬行动物的种类与鱼的种类之比为21∶4,已知两栖爬行动物比鱼的种类多34种,则两栖爬行动物有 种,鱼类有 种。
二、谨慎选择。(16分)
11.根据ab=cd(a、b、c、d均不为0),不一定能组成比例的是( )。
A.a:c=d:b B.d:a=b:c C.b:d=a:c D.a:d=c:b
12.一种精密零件长 3 毫米,把它画在比例尺是 12︰1 的图纸上,零件长应是 ( )厘米。
A.0.025 B.0.25 C.3.6 D.36
13.如果x=2y(x、y均不等于0),那么y:x=( )
A.2 B.2:1 C.1:2
14.一个长方形按4︰1放大后,得到的图形与原图形比较,下列说法中正确的是( )。
A.周长扩大16倍 B.周长缩小16倍 C.面积扩大16倍
15.哪组中的四个数不可以组成比例的是( )。
A.,,, B.1.4,2,28和40
C.8,,40和4 D.20,4,1和5
16.关于线段比例尺,下面说法正确的是( )。
A.图上距离是实际距离的
B.图上1 厘米表示实际距离2000000 厘米
C.实际距离是图上距离的40 倍
D.图上1 厘米表示实际距离40000 厘米
17. 一个比的前项是6,比值是 ,这个比的后项是 ( )。
A. B.10 C. D.
18.六(1)班人数在40到50之间,已知男生人数是女生人数的75%,全班最多有( )人。
A.42 B.45 C.49 D.50
三、细想快算。(20分)
19.求下面比的比值,并用下面的比组一组比例。
: 0.9: :0.75
20. 解方程或比例。
四、动手操作。(16分)
21.在下面的方格纸中分别画出把圆按2:1的比放大后的图形和把三角形按1:2 的比缩小后的图形。
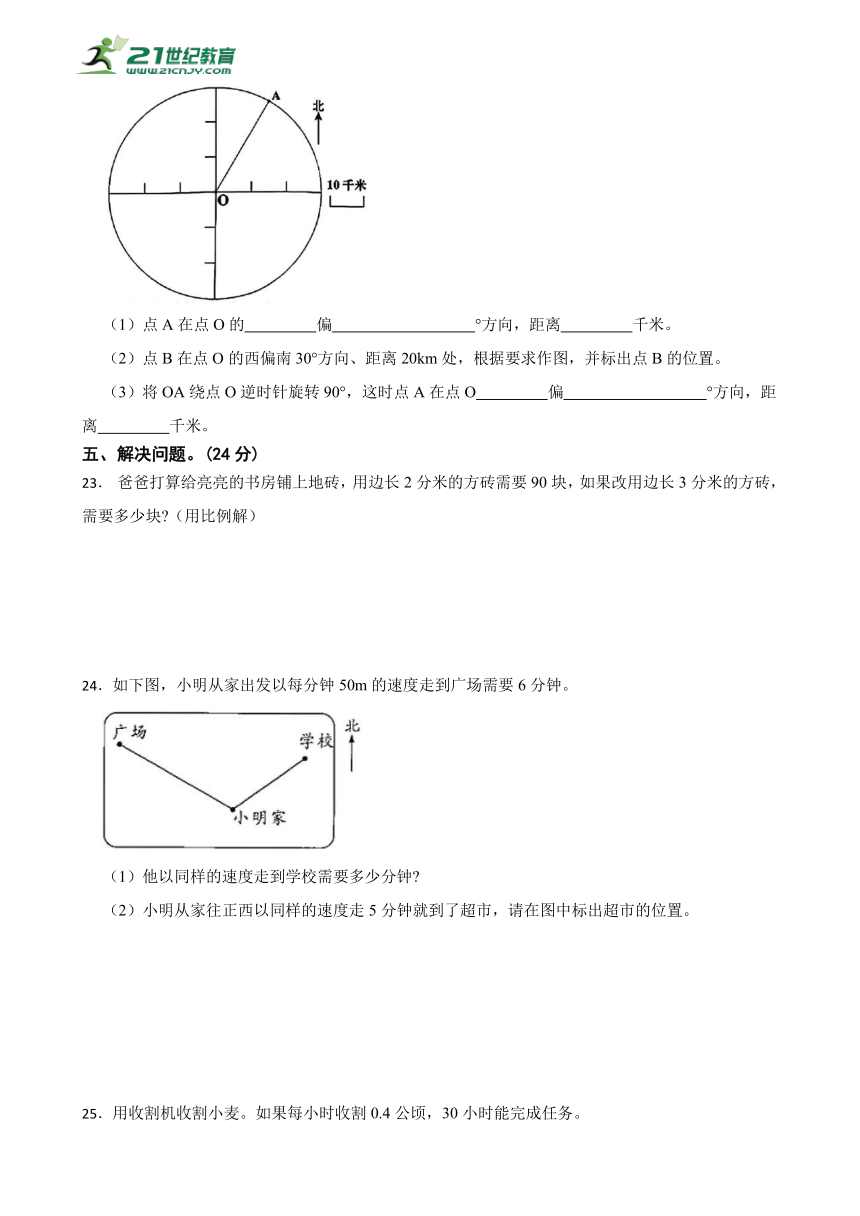
22.如下图,在某地以点O为圆心画一个很大的圆,点A是圆12等分后的一点。
(1)点A在点O的 偏 °方向,距离 千米。
(2)点B在点O的西偏南30°方向、距离20km处,根据要求作图,并标出点B的位置。
(3)将OA绕点O逆时针旋转90°,这时点A在点O 偏 °方向,距离 千米。
五、解决问题。(24分)
23. 爸爸打算给亮亮的书房铺上地砖,用边长2分米的方砖需要90块,如果改用边长3分米的方砖,需要多少块 (用比例解)
24.如下图,小明从家出发以每分钟50m的速度走到广场需要6分钟。
(1)他以同样的速度走到学校需要多少分钟
(2)小明从家往正西以同样的速度走5分钟就到了超市,请在图中标出超市的位置。
25.用收割机收割小麦。如果每小时收割0.4公顷,30小时能完成任务。
(1)现在想用20小时收割完,那么每小时应收割多少公顷?(用比例解答)
(2)你能提出其他数学问题并解答吗?
26. 在比例尺是1:6000000的地图上,A、B两地间的距离是16厘米。
(1)A、B两地间的实际距离是多少千米
(2)一列火车由A 地到B地用了4小时,火车每小时行多少千米
27.在比例尺为1:6000000的地图上,量得两地间的铁路长10cm。甲、乙两列火车同时从两地相对开出,3小时相遇。已知甲、乙两列火车行驶的路程比为11:9。
(1)两地间铁路的实际长度为多少千米?
(2)甲车每小时行驶多少千米?
六、附加题。(10分)
28.牧羊人赶着一群羊去放牧,跑走了一只公羊后,他发现剩下的羊中公羊和母羊的比是9:7.过了一会儿,跑走的公羊回到羊群,却又跑走了一只母羊,这时公羊与母羊的比是7:5.这群羊原来有多少只
答案解析部分
1.2、4.5、18
解:3×6÷9
=18÷9
=2;
3×9÷6
=27÷6
=4.5;
6×9÷3
=54÷3
=18。
故答案为:2、4.5、18。
比例的基本性质:在比例里,两个内项积等于两个外项积;
要求的数=其中两个数的积÷第三个数。
2.2:1;100
解:a:b=:=2:1;
(2-1)÷1
=1÷1
=100%。
故答案为:2:1;100。
比例的基本性质:在比例里,两个内项积等于两个外项积,因为×a=b×,所以 a:b=:=2:1; a比b多的百分率=(a-b)÷b。
3.4
解:1÷0.25=4
故答案为:4。
在比例里,两个内项的积等于两个外项的积。两个外项互为倒数,则两个内项也是互为倒数,所以用1除以一个内项即可求出另一个内项。
4.10;3:5=6:10
解:有3,5,6三个数,再添上一个数10可以组成比例,组成的比例是3:5=6:10。
故答案为:10;3:5=6:10。
表示两个比相等的式子叫比例。
5.37:10;3.7;每袋热干面的价格
解:18.5:5=37:10;
18.5:5=37:10=37÷10=3.7,这个比值表示每袋热干面的价格。
故答案为:37:10;3.7;每袋热干面的价格。
总价:数量=18.5:5,依据比的基本性质化简比;
求比值=比的前项÷比的后项;
总价÷数量=单价,这个比值表示每袋热干面的价格。
6.16
解:8÷=8×10000=80000(厘米)=800(米)
800÷50=16(分钟),他从家到学校要走16分钟。
故答案为:16。
图上距离÷比例尺=实际距离,实际距离÷小明的速度=小明走的时间。
7.2.4
120000千米=12000000000厘米
1200000000 × = 2.4(厘米)
故答案为:2.4。
图上距离=实际距离×比例尺,据此计算即可得出答案。
8.3
解: 240千米=24000000厘米
24000000×=3(厘米)
故答案为:3。
要求图上距离是多少厘米,根据“实际距离×比例尺=图上距离”,代入数值,计算即可
9.;6
解:4000000厘米=40千米
线段比例尺是;
240×100000×
=24000000×
=6(厘米)。
故答案为:;6。
实际距离=图上距离÷比例尺;比例尺=图上距离÷实际距离;图上距离=实际距离×比例尺。
10.42;8
解:(种),(种),50-42=8(种)。
故答案为:42,8。
本题考验对比的认知和比的应用,通过题目信息找到等量关系”保护区内两栖动物和鱼的总类的和= 两栖爬行动物比鱼的种类多的种类量÷“得到保护区内两栖动物和鱼的总类的和,然后再利用比的应用计算出二者的种类数量即可。
11.C
解:不一定能组成比例的是b:d=a:c。
故答案为:C。
在比例中,两个外项的积等于两个内项的积,据此作答即可。
12.C
解:3×12=36(毫米)=3.6厘米
故答案为:C。
根据图上距离=实际距离×比例尺,代入数值计算即可。
13.C
解:如果x=2y(x、y均不等于0),那么y:x=1:2。
故答案为:C。
在比例中,两内项积等于两外项积。
14.C
解:4×4=16, 面积扩大16倍。
故答案为:C。
得到图形的面积扩大的倍数=长方形长边扩大的倍数×长方形宽边扩大的倍数=4×4=16倍。
15.C
解:A、×=,所以能组成比例;
B、1.4×40=2×28,所以能组成比例;
C、8×=40×4=160;8×40=320×4=;8×4=32×40=16,所以这四个数不能组成比例;
D、20×1=4×5。
故答案为:C。
判断四个数能否组成比例可以根据比例的基本性质:两个内项的积等于两个外项的积,逆向思考只要能找到两组数字的积相等那么这四个数就可以组成比例,否则就不可以组成比例。
16.B
解:20千米=2000000厘米,
图上1 厘米表示实际距离2000000厘米 。
故答案为:B。
千米后面添上5个0化为米;线段比例尺的意思是图上1厘米表示实际距离2000000厘米。
17.B
解:6÷=10。
故答案为:B。
比的后项=比的前项÷比值。
18.C
解:75%=,
女生人数看做4份,男生人数看做3份,总人数是7份,
40到50之间7的最大的倍数是49,全班最多有49人。
故答案为:C。
全班的人数一定是总份数的倍数,据此解答。
19.解:÷=
0.9÷=1.5
÷0.75=
:=:0.75
比的比值=比的前项÷比的后项;
组成比例的两个比的比值相等。
20.x=6.4 x=5 x=1.5
21.解:
把一个圆按2:1放大,就是把半径扩大2倍,然后画圆即可;
把三角形按1:2缩小,就是把这个图形的每条边都缩小2倍。
22.(1)北;东;30;30
(2)解:
(3)西;北;30;30
解:(1)360°÷12=30°,3×10=30(千米)
所以,点A在点O的北偏东30°方向,距离30千米;
(2)20÷10=2(段)
①以O为顶点、OC边为角的一条边,偏向南方量取30°,并作好记号;
②连接记号与O点,并从O点开始量取两段线段长度,并在末端标上点“B”即可;
(3)将OA绕点O逆时针旋转90°,这时点A在点O西偏北30°方向,距离30千米。
故答案为:(1)北,东,30,30;(3)西,北,30,30。
(1)圆的圆心角是360°,12等分,即将圆心角平均分成12份,而点A只是其中的1份,所以OA与正北方的夹角=360°÷12;看图可知OA实际也是圆的半径,圆的半径平均分成3段,每段长10千米,所以OA=3×10=30(千米)。最后根据方向与距离确定物体位置的知识即可判断点A在点O的方向与距离;
(2)根据方向与距离确定物体的位置的知识:西偏南即以正西方为角的一条边,偏南方找角的另一条边画指定度数的角,再在偏南方的边上量出距离即可准确找到点B的位置;
(3)画按点旋转的方法 :①判断方向; ②把关键点与固定点相连; ③将连线作为角的一条边,固定点为顶点量角,画出另一条边; ④再在画出的角边上取出与连线同样长的一段线段的端点作为旋转点; ⑤同样的方法找出其他旋转点,最后依次把点用线相连即可作出旋转后的图形;最后再根据物体方向与距离的知识即可解答。
23.40块
24.(1)解:50×6=300(m)=30000cm
3cm:30000cm=1:10000
2÷=20000(cm)=200m
200÷50=4(分钟)
答:他以同样的速度走到学校需要4分钟。
(2)解:
(1)首先根据“路程=速度×时间”计算得出小明家到广场的实际距离为50×6=300(m),再根据1m=100cm,换算为30000cm,再用尺子分别测量出小明家与广场和学校的图上距离分别为3cm、2cm,然后根据“比例尺=图上距离:实际距离”,得出图中比例尺为3cm:30000cm=1:10000,最后用小明家到学校的图上距离除以比例尺得出小明家到学校的实际距离为2÷=20000(cm),换算单位后为200m,再根据“时间=路程÷速度”计算得到200÷50=4(分钟)即可;
(2)首先根据“路程=速度×时间”计算得出小明家到超市的实际距离为5×50=250(m),换算单位后为25000cm,然后根据“图上距离=实际距离×比例尺”计算得出小明家到超市的图上距离为25000×=2.5(cm),已知方向和图上距离,故可在图中标出超市的位置。
25.(1)解:设每小时应收割x公顷。
20x=0.4×30
20x=12
x=0.6
答:每小时应收割0.6公顷。
(2)解:实际平均每小时比计划平均每小时多收割多少公顷?
0.6-0.4=0.2(公顷)
答:实际平均每小时比计划平均每小时多收割0.2公顷。
(1)设每小时应收割x公顷。依据想用的时间×平均每小时应收割的面积=计划用的时间×计划平均每小时应收割的面积,列比例,解比例;
(2)实际平均每小时比计划平均每小时多收割的面积=实际平均每小时收割的面积 -计划平均每小时 收割的面积。
26.(1)解:16÷=96000000(厘米)
96000000厘米=960千米
答: A、B两地间的实际距离是960千米。
(2)解:960÷4=240(千米)
答: 火车每小时行240千米。
(1) 根据比例尺的定义,实际距离等于图上距离除以比例尺。
(2)路程÷时间=速度,据此解答。
27.(1)解:10÷ =60000000(厘米)
60000000厘米=600千米
答:两地间铁路的实际长度为600千米。
(2)解:600× ÷3
=330÷3
=110(千米)
答:甲车每小时行驶110千米。
(1)实际距离=图上距离÷比例尺;
(2)实际距离×=甲行驶的路程,甲行驶的路程÷甲行驶的时间=甲的速度。
28.解:
=49(只)
答:这群羊原来有49只。
分数问题,巧用单位“1”。把跑走1只羊后,剩下的两种羊的总数量看作单位“1”。如果以母羊为研究对象,跑走1只公羊后,母羊占剩下的两种羊的总数量的;跑走1只母羊后,剩下的母羊占剩下的两种羊的总数量的;从而可求出跑走1只羊后,剩下的两种羊的总数量,进而可求出原来这群羊的总数量。
考试范围:六下第二单元 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、细心填空。(24分)
1.一个数与3、6、9正好可以组成比例,那么这个数可能 。(不止一种情况,请写完整哟。)
2.如果×a=b×(a、b均不为0),则 a:b= ,a比b多 %。
3.在比例里,两个外项互为倒数,其中一个内项是0.25,另一个内项是 。
4.有3,5,6三个数,再添上一个数 可以组成比例,组成的比例是 。
5. 热干面是武汉市的一种特色小吃,妈妈网购了5袋热干面共花了18.5元,总价与数量最简单的整数比是 ,比值是 ,这个比值表示 。
6.在比例尺是1:10000的地图上,小明家到学校8厘米,如果小明每分钟走50米,他从家到学校要走 分钟。
7.甲、乙两地距高大约是120000千米,在比例尺是1:500000000的地图上, 长是 厘米。
8.实际距离240千米,画在比例尺是1:8000000的地图上,应画 厘米。
9.一幅地图的比例尺是1:4000000,把它改成线段比例尺是 ,已知AB两地的实际距离是240千米,在这幅地图上应画 厘米。
10.陕西牛背梁自然保护区被誉为物种的“天然基因库”,保护区内两栖爬行动物的种类与鱼的种类之比为21∶4,已知两栖爬行动物比鱼的种类多34种,则两栖爬行动物有 种,鱼类有 种。
二、谨慎选择。(16分)
11.根据ab=cd(a、b、c、d均不为0),不一定能组成比例的是( )。
A.a:c=d:b B.d:a=b:c C.b:d=a:c D.a:d=c:b
12.一种精密零件长 3 毫米,把它画在比例尺是 12︰1 的图纸上,零件长应是 ( )厘米。
A.0.025 B.0.25 C.3.6 D.36
13.如果x=2y(x、y均不等于0),那么y:x=( )
A.2 B.2:1 C.1:2
14.一个长方形按4︰1放大后,得到的图形与原图形比较,下列说法中正确的是( )。
A.周长扩大16倍 B.周长缩小16倍 C.面积扩大16倍
15.哪组中的四个数不可以组成比例的是( )。
A.,,, B.1.4,2,28和40
C.8,,40和4 D.20,4,1和5
16.关于线段比例尺,下面说法正确的是( )。
A.图上距离是实际距离的
B.图上1 厘米表示实际距离2000000 厘米
C.实际距离是图上距离的40 倍
D.图上1 厘米表示实际距离40000 厘米
17. 一个比的前项是6,比值是 ,这个比的后项是 ( )。
A. B.10 C. D.
18.六(1)班人数在40到50之间,已知男生人数是女生人数的75%,全班最多有( )人。
A.42 B.45 C.49 D.50
三、细想快算。(20分)
19.求下面比的比值,并用下面的比组一组比例。
: 0.9: :0.75
20. 解方程或比例。
四、动手操作。(16分)
21.在下面的方格纸中分别画出把圆按2:1的比放大后的图形和把三角形按1:2 的比缩小后的图形。
22.如下图,在某地以点O为圆心画一个很大的圆,点A是圆12等分后的一点。
(1)点A在点O的 偏 °方向,距离 千米。
(2)点B在点O的西偏南30°方向、距离20km处,根据要求作图,并标出点B的位置。
(3)将OA绕点O逆时针旋转90°,这时点A在点O 偏 °方向,距离 千米。
五、解决问题。(24分)
23. 爸爸打算给亮亮的书房铺上地砖,用边长2分米的方砖需要90块,如果改用边长3分米的方砖,需要多少块 (用比例解)
24.如下图,小明从家出发以每分钟50m的速度走到广场需要6分钟。
(1)他以同样的速度走到学校需要多少分钟
(2)小明从家往正西以同样的速度走5分钟就到了超市,请在图中标出超市的位置。
25.用收割机收割小麦。如果每小时收割0.4公顷,30小时能完成任务。
(1)现在想用20小时收割完,那么每小时应收割多少公顷?(用比例解答)
(2)你能提出其他数学问题并解答吗?
26. 在比例尺是1:6000000的地图上,A、B两地间的距离是16厘米。
(1)A、B两地间的实际距离是多少千米
(2)一列火车由A 地到B地用了4小时,火车每小时行多少千米
27.在比例尺为1:6000000的地图上,量得两地间的铁路长10cm。甲、乙两列火车同时从两地相对开出,3小时相遇。已知甲、乙两列火车行驶的路程比为11:9。
(1)两地间铁路的实际长度为多少千米?
(2)甲车每小时行驶多少千米?
六、附加题。(10分)
28.牧羊人赶着一群羊去放牧,跑走了一只公羊后,他发现剩下的羊中公羊和母羊的比是9:7.过了一会儿,跑走的公羊回到羊群,却又跑走了一只母羊,这时公羊与母羊的比是7:5.这群羊原来有多少只
答案解析部分
1.2、4.5、18
解:3×6÷9
=18÷9
=2;
3×9÷6
=27÷6
=4.5;
6×9÷3
=54÷3
=18。
故答案为:2、4.5、18。
比例的基本性质:在比例里,两个内项积等于两个外项积;
要求的数=其中两个数的积÷第三个数。
2.2:1;100
解:a:b=:=2:1;
(2-1)÷1
=1÷1
=100%。
故答案为:2:1;100。
比例的基本性质:在比例里,两个内项积等于两个外项积,因为×a=b×,所以 a:b=:=2:1; a比b多的百分率=(a-b)÷b。
3.4
解:1÷0.25=4
故答案为:4。
在比例里,两个内项的积等于两个外项的积。两个外项互为倒数,则两个内项也是互为倒数,所以用1除以一个内项即可求出另一个内项。
4.10;3:5=6:10
解:有3,5,6三个数,再添上一个数10可以组成比例,组成的比例是3:5=6:10。
故答案为:10;3:5=6:10。
表示两个比相等的式子叫比例。
5.37:10;3.7;每袋热干面的价格
解:18.5:5=37:10;
18.5:5=37:10=37÷10=3.7,这个比值表示每袋热干面的价格。
故答案为:37:10;3.7;每袋热干面的价格。
总价:数量=18.5:5,依据比的基本性质化简比;
求比值=比的前项÷比的后项;
总价÷数量=单价,这个比值表示每袋热干面的价格。
6.16
解:8÷=8×10000=80000(厘米)=800(米)
800÷50=16(分钟),他从家到学校要走16分钟。
故答案为:16。
图上距离÷比例尺=实际距离,实际距离÷小明的速度=小明走的时间。
7.2.4
120000千米=12000000000厘米
1200000000 × = 2.4(厘米)
故答案为:2.4。
图上距离=实际距离×比例尺,据此计算即可得出答案。
8.3
解: 240千米=24000000厘米
24000000×=3(厘米)
故答案为:3。
要求图上距离是多少厘米,根据“实际距离×比例尺=图上距离”,代入数值,计算即可
9.;6
解:4000000厘米=40千米
线段比例尺是;
240×100000×
=24000000×
=6(厘米)。
故答案为:;6。
实际距离=图上距离÷比例尺;比例尺=图上距离÷实际距离;图上距离=实际距离×比例尺。
10.42;8
解:(种),(种),50-42=8(种)。
故答案为:42,8。
本题考验对比的认知和比的应用,通过题目信息找到等量关系”保护区内两栖动物和鱼的总类的和= 两栖爬行动物比鱼的种类多的种类量÷“得到保护区内两栖动物和鱼的总类的和,然后再利用比的应用计算出二者的种类数量即可。
11.C
解:不一定能组成比例的是b:d=a:c。
故答案为:C。
在比例中,两个外项的积等于两个内项的积,据此作答即可。
12.C
解:3×12=36(毫米)=3.6厘米
故答案为:C。
根据图上距离=实际距离×比例尺,代入数值计算即可。
13.C
解:如果x=2y(x、y均不等于0),那么y:x=1:2。
故答案为:C。
在比例中,两内项积等于两外项积。
14.C
解:4×4=16, 面积扩大16倍。
故答案为:C。
得到图形的面积扩大的倍数=长方形长边扩大的倍数×长方形宽边扩大的倍数=4×4=16倍。
15.C
解:A、×=,所以能组成比例;
B、1.4×40=2×28,所以能组成比例;
C、8×=40×4=160;8×40=320×4=;8×4=32×40=16,所以这四个数不能组成比例;
D、20×1=4×5。
故答案为:C。
判断四个数能否组成比例可以根据比例的基本性质:两个内项的积等于两个外项的积,逆向思考只要能找到两组数字的积相等那么这四个数就可以组成比例,否则就不可以组成比例。
16.B
解:20千米=2000000厘米,
图上1 厘米表示实际距离2000000厘米 。
故答案为:B。
千米后面添上5个0化为米;线段比例尺的意思是图上1厘米表示实际距离2000000厘米。
17.B
解:6÷=10。
故答案为:B。
比的后项=比的前项÷比值。
18.C
解:75%=,
女生人数看做4份,男生人数看做3份,总人数是7份,
40到50之间7的最大的倍数是49,全班最多有49人。
故答案为:C。
全班的人数一定是总份数的倍数,据此解答。
19.解:÷=
0.9÷=1.5
÷0.75=
:=:0.75
比的比值=比的前项÷比的后项;
组成比例的两个比的比值相等。
20.x=6.4 x=5 x=1.5
21.解:
把一个圆按2:1放大,就是把半径扩大2倍,然后画圆即可;
把三角形按1:2缩小,就是把这个图形的每条边都缩小2倍。
22.(1)北;东;30;30
(2)解:
(3)西;北;30;30
解:(1)360°÷12=30°,3×10=30(千米)
所以,点A在点O的北偏东30°方向,距离30千米;
(2)20÷10=2(段)
①以O为顶点、OC边为角的一条边,偏向南方量取30°,并作好记号;
②连接记号与O点,并从O点开始量取两段线段长度,并在末端标上点“B”即可;
(3)将OA绕点O逆时针旋转90°,这时点A在点O西偏北30°方向,距离30千米。
故答案为:(1)北,东,30,30;(3)西,北,30,30。
(1)圆的圆心角是360°,12等分,即将圆心角平均分成12份,而点A只是其中的1份,所以OA与正北方的夹角=360°÷12;看图可知OA实际也是圆的半径,圆的半径平均分成3段,每段长10千米,所以OA=3×10=30(千米)。最后根据方向与距离确定物体位置的知识即可判断点A在点O的方向与距离;
(2)根据方向与距离确定物体的位置的知识:西偏南即以正西方为角的一条边,偏南方找角的另一条边画指定度数的角,再在偏南方的边上量出距离即可准确找到点B的位置;
(3)画按点旋转的方法 :①判断方向; ②把关键点与固定点相连; ③将连线作为角的一条边,固定点为顶点量角,画出另一条边; ④再在画出的角边上取出与连线同样长的一段线段的端点作为旋转点; ⑤同样的方法找出其他旋转点,最后依次把点用线相连即可作出旋转后的图形;最后再根据物体方向与距离的知识即可解答。
23.40块
24.(1)解:50×6=300(m)=30000cm
3cm:30000cm=1:10000
2÷=20000(cm)=200m
200÷50=4(分钟)
答:他以同样的速度走到学校需要4分钟。
(2)解:
(1)首先根据“路程=速度×时间”计算得出小明家到广场的实际距离为50×6=300(m),再根据1m=100cm,换算为30000cm,再用尺子分别测量出小明家与广场和学校的图上距离分别为3cm、2cm,然后根据“比例尺=图上距离:实际距离”,得出图中比例尺为3cm:30000cm=1:10000,最后用小明家到学校的图上距离除以比例尺得出小明家到学校的实际距离为2÷=20000(cm),换算单位后为200m,再根据“时间=路程÷速度”计算得到200÷50=4(分钟)即可;
(2)首先根据“路程=速度×时间”计算得出小明家到超市的实际距离为5×50=250(m),换算单位后为25000cm,然后根据“图上距离=实际距离×比例尺”计算得出小明家到超市的图上距离为25000×=2.5(cm),已知方向和图上距离,故可在图中标出超市的位置。
25.(1)解:设每小时应收割x公顷。
20x=0.4×30
20x=12
x=0.6
答:每小时应收割0.6公顷。
(2)解:实际平均每小时比计划平均每小时多收割多少公顷?
0.6-0.4=0.2(公顷)
答:实际平均每小时比计划平均每小时多收割0.2公顷。
(1)设每小时应收割x公顷。依据想用的时间×平均每小时应收割的面积=计划用的时间×计划平均每小时应收割的面积,列比例,解比例;
(2)实际平均每小时比计划平均每小时多收割的面积=实际平均每小时收割的面积 -计划平均每小时 收割的面积。
26.(1)解:16÷=96000000(厘米)
96000000厘米=960千米
答: A、B两地间的实际距离是960千米。
(2)解:960÷4=240(千米)
答: 火车每小时行240千米。
(1) 根据比例尺的定义,实际距离等于图上距离除以比例尺。
(2)路程÷时间=速度,据此解答。
27.(1)解:10÷ =60000000(厘米)
60000000厘米=600千米
答:两地间铁路的实际长度为600千米。
(2)解:600× ÷3
=330÷3
=110(千米)
答:甲车每小时行驶110千米。
(1)实际距离=图上距离÷比例尺;
(2)实际距离×=甲行驶的路程,甲行驶的路程÷甲行驶的时间=甲的速度。
28.解:
=49(只)
答:这群羊原来有49只。
分数问题,巧用单位“1”。把跑走1只羊后,剩下的两种羊的总数量看作单位“1”。如果以母羊为研究对象,跑走1只公羊后,母羊占剩下的两种羊的总数量的;跑走1只母羊后,剩下的母羊占剩下的两种羊的总数量的;从而可求出跑走1只羊后,剩下的两种羊的总数量,进而可求出原来这群羊的总数量。
