2024-2025年人教版五年级下册数学第一单元观察物体(三)单元提升训练(含解析)
文档属性
| 名称 | 2024-2025年人教版五年级下册数学第一单元观察物体(三)单元提升训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-07 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学第一单元观察物体(三)单元提升训练
一、填空题
1.一个几何体从上面、前面、左面看到的形状都是,搭成这个几何体要( )个小正方体。
2.一个由相同的小正方体摆成的几何体,从上面看到的是,数字表示这个位置所用的小正方体个数。这个几何体从左面看到的形状是图( )(填“甲”或“乙”)。
3.中国象棋源远流长,是中华民族的文化瑰宝。佳佳从小喜欢下象棋,她在桌面上用象棋摆了一个形状。下面是她从三个方向所看到的图形,佳佳摆这个形状最少要用( )枚象棋,最多要用( )枚象棋。
4.一个由小正方体搭成的几何体,从前面看,从左面看,从上面看,这个几何图形是由( )个小正方体搭成的。
5.用4个同样的小正方体摆成一个几何体,摆成两行,从前面看是,有( )种不同的摆法。
6.给增加一个小正方体,若从前面看图形不变,则有( )种摆法。
7.用8个同样的小正方体摆成一个大正方体,如图所示,最多拿走( )个小正方体后,还能保证从前面、上面和左面看到的图形都是。
8.下图要保持从上面看到的图形不变,最多可以拿掉( )个小正方体。
9.把6个棱长是1cm的小正方体拼摆在一起(如图),如果从前面、上面和左面看,所看到的图形面积之和是( )cm2。
10.一个立体图形,从上面看到的形状是,从左面看到的形状是,搭这样的立体图形,最少需要( )个小正方体,最多可以有( )个小正方体。
二、选择题
11.下面4个几何体中,从上面和前面看到的图形相同的是( )。
A. B.
C. D.
12.由若干个小正方体搭成的几何体,从左面看和从正面看,看到的形状如下图所示,要搭成这样的几何体最多需要( )个小正方体。
A.7 B.8 C.10 D.12
13.用同样的小正方体搭一个几何体,从上面看到的图形如图(每个正方形上面的数字表示这个位置上所用小正方体的个数)。这个几何体从左面看是( )。
A. B. C. D.
14.用5个正方体搭成一个几何体,从正面看是,从上面看是,从右面看是,这个几何体是( )。
A. B. C. D.
15.从不同的方向观察如图所示的几何体,有以下4个图案:其中不可能看到的图案是( )。
A.① B.② C.③ D.④
16.花花用5个同样的小正方体摆一个几何体,从上面看是,从左面看是。一共有( )种不同的摆法。
A.4 B.3 C.2 D.1
三、作图题
17.分别画出下面的立体图形从上面、正面、左面看到的形状。
四、解答题
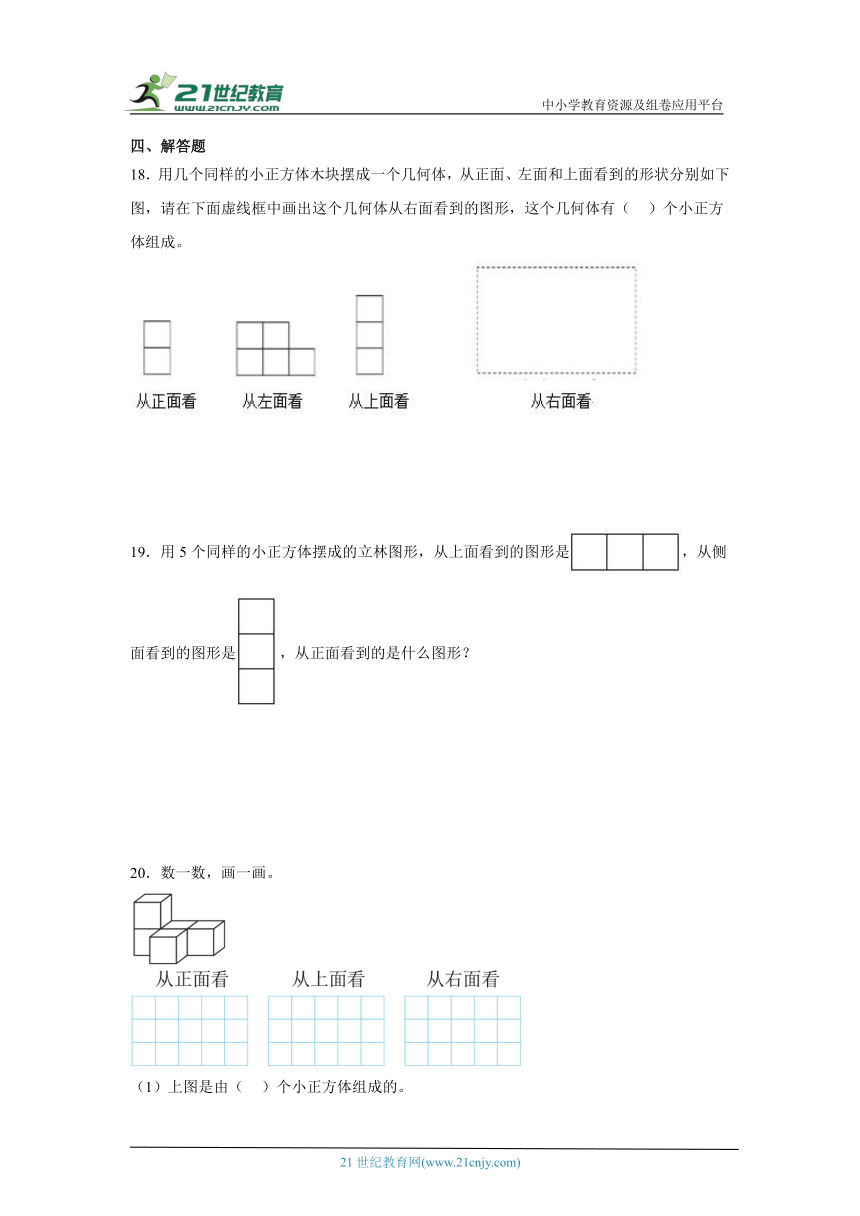
18.用几个同样的小正方体木块摆成一个几何体,从正面、左面和上面看到的形状分别如下图,请在下面虚线框中画出这个几何体从右面看到的图形,这个几何体有( )个小正方体组成。
19.用5个同样的小正方体摆成的立林图形,从上面看到的图形是,从侧面看到的图形是,从正面看到的是什么图形?
20.数一数,画一画。
(1)上图是由( )个小正方体组成的。
(2)分别画出从正面、上面和右面看到的形状。
21.搭一个这样的立体图形最少需要几个小正方体?最多可以有几个小正方体?
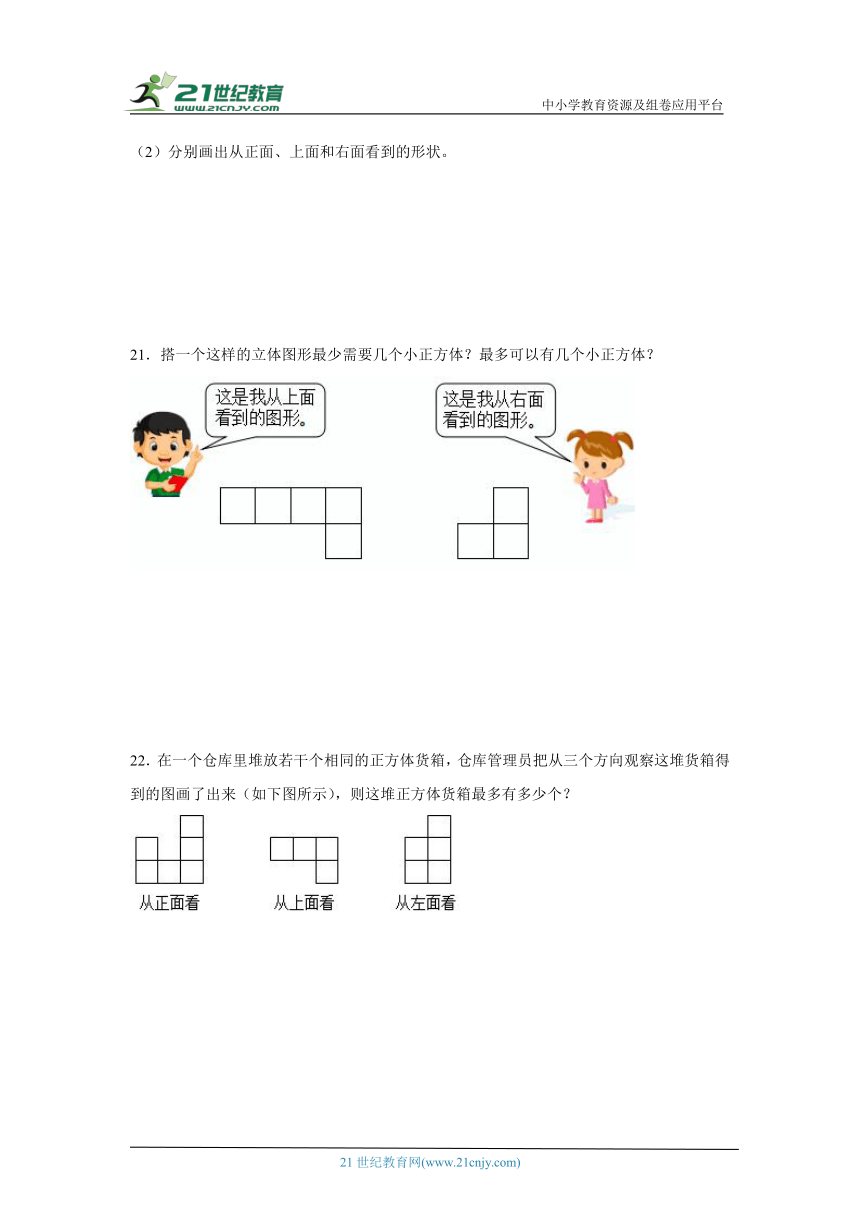
22.在一个仓库里堆放若干个相同的正方体货箱,仓库管理员把从三个方向观察这堆货箱得到的图画了出来(如下图所示),则这堆正方体货箱最多有多少个?
23.将几个大小相同的正方体木块放成一堆,图1至图3分别对应该图形从上面、正面、左面看到的图形,则这堆木块共有多少块?
24.从前面观察一个由同样的小正方体组成的几何体,看到的图形如下图,这个几何体可能是怎样摆的?
(1)这个几何体如果是由4个小正方体组成的,可以怎样摆?
(2)这个几何体如果是由5个、6个、7个或更多的小正方体组成的,可以怎样摆?
25.用棱长是1cm的小正方体靠墙角摆成如图所示的几何体。
(1)摆这个几何体一共用了多少个小正方体?
(2)从图中取走( )号小正方体后,从正面、上面、右面看到的图形不变。
26.下面是用小正方体搭建的一些几何体。
(1)从正面看到的是的有( ),从侧面看到的是的有( ),从上面看到的是的有( )。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,有多少种不同的摆法?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
《2024-2025年人教版五年级下册数学第一单元观察物体(三)单元提升训练》参考答案
1.4
【分析】根据从上面、前面、左面看到的形状可知,这个几何体有两层,下层有2排,前面一排有2个小正方体,后面一排有1个小正方体,且居左;上层有1个小正方体,且居左;据此得出搭成这个几何体需要小正方体的个数。
【详解】如图:
搭成这个几何体要4个小正方体。
2.乙
【分析】从上面看到的平面图形可以确定小正方体的位置,所有数字的和就是小正方体的数量;由上面看到的平面图形可知,从左面可以看到两列,左边一列可以看到2个小正方形,右边一列可以看到3个小正方形,据此解答。
【详解】
一个由相同的小正方体摆成的几何体,从上面看到的是,数字表示这个位置所用的小正方体个数。这个几何体从左面看到的形状是图乙。
3. 8 10
【分析】根据从上面看到形状可知,底层有3枚象棋,结合从前面和右面看到的形状可知, “车”有4枚, “马”有3枚, “兵”至少有1枚,最多有3枚,据此解答即可。
【详解】3+4+3=10(个)
3+4+1=8(个)
由分析可知,如图是她从三个方向所看到的图形,佳佳摆这个形状最少要用8枚象棋,最多要用10枚象棋。
4.6
【分析】从上面看可以确定第一层有5个小正方体,从前面和左面看,可以确定第二层有1个小正方体,再把这两层的小正方体的个数相加起来即可。
【详解】(个)
所以这个几何图形是由6个小正方体搭成的。
5.6
【分析】要使得从前面看是这个图形,那么一共有6种不同的摆法。
如图:
【详解】
根据分析可知用4个同样的小正方体摆成一个几何体,摆成两行,从前面看是, 所以,有6种不同的摆法。
6.6
【分析】从前面看有一排,3个小正方形,增加一个小正方体,可以摆在任意小正方体的前、后面,放前面有3种方法,放后面有3种方法,一共有3+3=6种摆放。
【详解】3+3=6(种)
给增加一个小正方体,若从前面看图形不变,则有6种摆法。
7.2
【分析】根据遮挡关系,上层对着角拿走2个正方体,从前面、上面和左面看到的图形不变,据此分析。
【详解】
上层对角拿走2个小正方体,从上面看摆法如图:或,最多拿走2个小正方体后,还能保证从前面、上面和左面看到的图形都是。
8.4
【分析】观察,从上面看到的图形是,要保持从上面看到的图形不变,只能拿第二层和第三层的小正方体,第二层有3个小正方体,第三层有1个小正方体,全部拿走后,从上面看到的图形依然不变,据此解答。
【详解】根据分析得,3+1=4(个)
最多可以拿掉4个小正方体,从上面看到的图形不变。
【点睛】此题主要考查学生的空间想象力,根据观察立体图形的方法,做出正确的解答。
9.12
【分析】观察图形可知,从前面能看到4个小正方形,从上面能看到5个小正方形,从左面能看到3个小正方形,则一共看到(4+5+3)个小正方形;
根据正方形的面积=边长×边长,求出一个面的面积,再乘从前面、上面和左面看到小正方形的个数即可。
【详解】1×1=1(cm2)
1×(4+5+3)
=1×12
=12(cm2)
如果从前面、上面和左面看,所看到的图形面积之和是12cm2。
【点睛】本题考查从不同方向观察立体图形,从前面、上面、左面这三个方向正确数出看到的小正方形的个数是解题的关键。
10. 5 7
【分析】从上面看到的图形可得,这个图形底层前面一行1个小正方体,后面一行3个正方体,所以至少有4个小正方体;
从左面看到的图形可得,前面一行只有1层,所以前面一行只有1个正方形,后面一行是2层,要使小正方体最少,则上层只有1个正方体;要使小正方体最多,则上层是3个正方体。
【详解】最少有:4+1=5(个)
最多有:4+3=7(个)
搭这样的立体图形,最少需要5个小正方体,最多可以有7个小正方体。
11.A
【分析】A.从上面看有2行,下边1行3个小正方形,上边1行靠右1个小正方形;从前面看有2行,下边1行3个小正方形,上边1行靠右1个小正方形;
B.从上面看有2行,上边1行3个小正方形,下边1行靠右1个小正方形;从前面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;
C.从上面看有2行,上边1行3个小正方形,下边1行中间1个小正方形;从前面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;
D.从上面看是1行3个小正方形;从前面看有2行,下边1行3个小正方形,上边1行中间1个小正方形。
【详解】
A.从上面看到的图形是,从前面看到的图形是;
B.从上面看到的图形是,从前面看到的图形是;
C.从上面看到的图形是,从前面看到的图形是;
D.从上面看到的图形是,从前面看到的图形是。
从上面和前面看到的图形相同的是,都是。
故答案为:A
12.C
【分析】根据从左面看的图形,可知立体图形有三行两层;根据从正面看的图形,可知立体图形有三列两层;综合以上,则第二行第二列处必须上下重叠摆放2个小正方体,据此试着拼摆这个立体图形,并数出最多需要几个小正方体即可。
【详解】符合从左面、正面看到的图形,最少需要的小正方体块数如图1所示,最多需要的小正方体块数如图2所示,所以要搭成这样的几何体最多需要10个小正方体。
故答案为:C
13.C
【分析】
根据从上面看到的形状和数字,可以确定这个几何体如图,从左面看有3行,下边1行3个小正方形;中间1行2个小正方形,左对齐;上边1行1个小正方形,居中;据此分析。
【详解】
根据分析,这个几何体从左面看是。
故答案为:C
14.C
【分析】A.从正面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;从上面看有2列,右边1列3个小正方形,左边1列靠上1个小正方形;从右面看有2行,下边1行3个小正方形,上边1行靠右1个小正方形;
B.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;
C.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,上边1行3个小正方形,下边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形;
D.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,上边1行3个小正方形,下边1行靠左1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形。
【详解】
A.从正面看是,从上面看是,从右面看是;
B.从正面看是,从上面看是,从右面看是;
C.从正面看是,从上面看是,从右面看是;
D.从正面看是,从上面看是,从右面看是。
用5个正方体搭成一个几何体,从正面看是,从上面看是,从右面看是,这个几何体是。
故答案为:C
15.B
【分析】从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;从上面看有2行,前边1行3个小正方形,后边1行靠右1个小正方形。
【详解】
从正面看到的是,从左面看到的是,从上面看到的是。
不可能看到的图案是。
故答案为:B
16.B
【分析】根据从上面看到的形状,可以确定底层有4个小正方体,以及这4个小正方体的摆放位置;根据从左面看到的形状,可以确定第二层的1个小正方体只能摆到并排的3个小正方体的上面,据此分析。
【详解】
如图,一共有3种不同的摆法。
故答案为:B
17.见详解
【分析】观察图形可知,从上面看到的是2层:上层3个正方形,下层1个正方形靠右边;从正面看到的是2层:下层3个正方形,上层1个正方形靠右边;从左面看到的图形是2层:下层2个正方形,上层1个正方形靠左边。
【详解】
18.作图见详解;5
【分析】根据从正面、左面、上面看到的形状,确定几何体如图,右面看到的图形与左面看到的图形左右相反,据此画出右面看到的图形,数出小正方体数量即可。
【详解】从右面看是,这个几何体有5个小正方体组成。
【点睛】观察一个用小正方体搭建的立方体图形,发现从不同的位置观察到图形的形状可能是不同的。
19.;;
【详解】用5个同样的小正方体摆成的立林图形,有3种拼法:
所以从正面看到的分别是;;。
答:从正面看到的分别是;; 。
【点睛】此题可以把从不同方向看到的平面图形进行综合分析,从而确定立体图形的形状。
20.(1)5
(2)见详解
【分析】(1)观察几何体,用小正方体摆了2层,底层4个小正方体,上层1个小正方体,共5个小正方体组成;
(2)从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,前边1行3个小正方形,后边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形。
【详解】(1)观察可知,上图是由5个小正方体组成的。
(2)
21.最少需要6个小正方体,最多可以有9个小正方体。
【解析】略
22.8个
【分析】由主视图,我们可以观察到行数最多为3行,列数最多为3列,由左到右,货箱个数呈2、1、3排列;接着看俯视图,共有2行,其中排在靠前一行只有一个货箱,位于右下角,结合主视图,我们基本可以确定,刚才呈2、1排列的货箱位于靠后一行,至于那竖直的3个货箱,要结合左视图确定;从左面看,共有2列,第1列竖直2个,第2列竖直3个。至此我们可以总结出:从左面看第1列的2个决定了组合体后一排最高只有2个,前排最高只有3个,而且最后一排左边最多有2个,中间1个,右边最多有2个。
【详解】 2+1+2+3=8(个)
答:这堆正方体货箱最多有8个。
【点睛】本题难度较大,需要一边观察三视图,一边想象立体图形的样子。在反复试验中一步步确定货箱的个数。并且题目给的三视图确定的几何体并不唯一,我们所求的是最多的那一种。
23.9块
【分析】由从上向下看到的视图易得最底层小正方体的个数,由从正面看到的视图和从左向右看到的视图找到其余层数里小正方体的个数相加即可。
【详解】如图:
由从上向下看到的视图易得最底层有6个小正方体,第二层最多也有2个小正方体,第二层最多也有1个小正方体,
所以这堆木块最多共有
6+2+1
=8+1
=9(块)
答:这堆木块共有9块。
【点睛】考查了从不同方向观察物体和几何体,解答此题应注意从上向下看到的视图决定底层正方体的个数。
24.见详解
【分析】
无论用4个、5个、6个、7个或更多的小正方体组成的几何体,从前面看到的形状都是,只要满足这个条件即可。
【详解】(1)这个几何体如果是由4个小正方体组成的,可以这样摆,如图:
(答案不唯一)
(2)这个几何体如果是由5个、6个、7个小正方体或更多的小正方体组成的,可以这样摆,如图:
(答案不唯一)
25.(1)20个
(2)5
【分析】从下往上一层一层数,然后加起来即可;第一层:10个,第二层:1+2+3=6(个),第三层:1+2=3(个),第四层:1个,一共10+6+3+1=10(个),据此解答;
(2)从图中取走1个小正方体后,从正面、上面、右面看到的图形不变,那么这个小正方体必须有3面,即后面、下面、左面都与其他正方体接触,这样拿走它从正面、上面、右面看到的图形不变,所以这个小正方体是5号。
【详解】由分析可知:
(1)10+(1+2+3)+(1+2)+1
=10+6+3+1
=16+3+1
=20(个)
答:这个几何体一共有20个小正方体。
(2)从图中取走5号小正方体后,从正面、上面、右面看到的图形不变。
26.(1)④⑤;①③;④
(2)5
【分析】(1)从正面看到的是二行,最下面一行三个小正方形并排,上面一行一个放在中间;从侧面看是一列两个,上下排列;从上面看是二行三列,上下行各两个正方形,呈“Z”型排列。由此分析判断。
(2)几何体⑥从正面看到的形状如右: ,根据此图,展开想象,确定物体的形状。
【详解】
(1)从正面看到的是的有(④⑤),从侧面看到的是的有(①③),从上面看到的是的有(④)。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,可以有如下摆法。
共有5种。
【点睛】掌握物体三视体的画法及根据物体三视图确定物体的形状是解答的关键。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学第一单元观察物体(三)单元提升训练
一、填空题
1.一个几何体从上面、前面、左面看到的形状都是,搭成这个几何体要( )个小正方体。
2.一个由相同的小正方体摆成的几何体,从上面看到的是,数字表示这个位置所用的小正方体个数。这个几何体从左面看到的形状是图( )(填“甲”或“乙”)。
3.中国象棋源远流长,是中华民族的文化瑰宝。佳佳从小喜欢下象棋,她在桌面上用象棋摆了一个形状。下面是她从三个方向所看到的图形,佳佳摆这个形状最少要用( )枚象棋,最多要用( )枚象棋。
4.一个由小正方体搭成的几何体,从前面看,从左面看,从上面看,这个几何图形是由( )个小正方体搭成的。
5.用4个同样的小正方体摆成一个几何体,摆成两行,从前面看是,有( )种不同的摆法。
6.给增加一个小正方体,若从前面看图形不变,则有( )种摆法。
7.用8个同样的小正方体摆成一个大正方体,如图所示,最多拿走( )个小正方体后,还能保证从前面、上面和左面看到的图形都是。
8.下图要保持从上面看到的图形不变,最多可以拿掉( )个小正方体。
9.把6个棱长是1cm的小正方体拼摆在一起(如图),如果从前面、上面和左面看,所看到的图形面积之和是( )cm2。
10.一个立体图形,从上面看到的形状是,从左面看到的形状是,搭这样的立体图形,最少需要( )个小正方体,最多可以有( )个小正方体。
二、选择题
11.下面4个几何体中,从上面和前面看到的图形相同的是( )。
A. B.
C. D.
12.由若干个小正方体搭成的几何体,从左面看和从正面看,看到的形状如下图所示,要搭成这样的几何体最多需要( )个小正方体。
A.7 B.8 C.10 D.12
13.用同样的小正方体搭一个几何体,从上面看到的图形如图(每个正方形上面的数字表示这个位置上所用小正方体的个数)。这个几何体从左面看是( )。
A. B. C. D.
14.用5个正方体搭成一个几何体,从正面看是,从上面看是,从右面看是,这个几何体是( )。
A. B. C. D.
15.从不同的方向观察如图所示的几何体,有以下4个图案:其中不可能看到的图案是( )。
A.① B.② C.③ D.④
16.花花用5个同样的小正方体摆一个几何体,从上面看是,从左面看是。一共有( )种不同的摆法。
A.4 B.3 C.2 D.1
三、作图题
17.分别画出下面的立体图形从上面、正面、左面看到的形状。
四、解答题
18.用几个同样的小正方体木块摆成一个几何体,从正面、左面和上面看到的形状分别如下图,请在下面虚线框中画出这个几何体从右面看到的图形,这个几何体有( )个小正方体组成。
19.用5个同样的小正方体摆成的立林图形,从上面看到的图形是,从侧面看到的图形是,从正面看到的是什么图形?
20.数一数,画一画。
(1)上图是由( )个小正方体组成的。
(2)分别画出从正面、上面和右面看到的形状。
21.搭一个这样的立体图形最少需要几个小正方体?最多可以有几个小正方体?
22.在一个仓库里堆放若干个相同的正方体货箱,仓库管理员把从三个方向观察这堆货箱得到的图画了出来(如下图所示),则这堆正方体货箱最多有多少个?
23.将几个大小相同的正方体木块放成一堆,图1至图3分别对应该图形从上面、正面、左面看到的图形,则这堆木块共有多少块?
24.从前面观察一个由同样的小正方体组成的几何体,看到的图形如下图,这个几何体可能是怎样摆的?
(1)这个几何体如果是由4个小正方体组成的,可以怎样摆?
(2)这个几何体如果是由5个、6个、7个或更多的小正方体组成的,可以怎样摆?
25.用棱长是1cm的小正方体靠墙角摆成如图所示的几何体。
(1)摆这个几何体一共用了多少个小正方体?
(2)从图中取走( )号小正方体后,从正面、上面、右面看到的图形不变。
26.下面是用小正方体搭建的一些几何体。
(1)从正面看到的是的有( ),从侧面看到的是的有( ),从上面看到的是的有( )。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,有多少种不同的摆法?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
《2024-2025年人教版五年级下册数学第一单元观察物体(三)单元提升训练》参考答案
1.4
【分析】根据从上面、前面、左面看到的形状可知,这个几何体有两层,下层有2排,前面一排有2个小正方体,后面一排有1个小正方体,且居左;上层有1个小正方体,且居左;据此得出搭成这个几何体需要小正方体的个数。
【详解】如图:
搭成这个几何体要4个小正方体。
2.乙
【分析】从上面看到的平面图形可以确定小正方体的位置,所有数字的和就是小正方体的数量;由上面看到的平面图形可知,从左面可以看到两列,左边一列可以看到2个小正方形,右边一列可以看到3个小正方形,据此解答。
【详解】
一个由相同的小正方体摆成的几何体,从上面看到的是,数字表示这个位置所用的小正方体个数。这个几何体从左面看到的形状是图乙。
3. 8 10
【分析】根据从上面看到形状可知,底层有3枚象棋,结合从前面和右面看到的形状可知, “车”有4枚, “马”有3枚, “兵”至少有1枚,最多有3枚,据此解答即可。
【详解】3+4+3=10(个)
3+4+1=8(个)
由分析可知,如图是她从三个方向所看到的图形,佳佳摆这个形状最少要用8枚象棋,最多要用10枚象棋。
4.6
【分析】从上面看可以确定第一层有5个小正方体,从前面和左面看,可以确定第二层有1个小正方体,再把这两层的小正方体的个数相加起来即可。
【详解】(个)
所以这个几何图形是由6个小正方体搭成的。
5.6
【分析】要使得从前面看是这个图形,那么一共有6种不同的摆法。
如图:
【详解】
根据分析可知用4个同样的小正方体摆成一个几何体,摆成两行,从前面看是, 所以,有6种不同的摆法。
6.6
【分析】从前面看有一排,3个小正方形,增加一个小正方体,可以摆在任意小正方体的前、后面,放前面有3种方法,放后面有3种方法,一共有3+3=6种摆放。
【详解】3+3=6(种)
给增加一个小正方体,若从前面看图形不变,则有6种摆法。
7.2
【分析】根据遮挡关系,上层对着角拿走2个正方体,从前面、上面和左面看到的图形不变,据此分析。
【详解】
上层对角拿走2个小正方体,从上面看摆法如图:或,最多拿走2个小正方体后,还能保证从前面、上面和左面看到的图形都是。
8.4
【分析】观察,从上面看到的图形是,要保持从上面看到的图形不变,只能拿第二层和第三层的小正方体,第二层有3个小正方体,第三层有1个小正方体,全部拿走后,从上面看到的图形依然不变,据此解答。
【详解】根据分析得,3+1=4(个)
最多可以拿掉4个小正方体,从上面看到的图形不变。
【点睛】此题主要考查学生的空间想象力,根据观察立体图形的方法,做出正确的解答。
9.12
【分析】观察图形可知,从前面能看到4个小正方形,从上面能看到5个小正方形,从左面能看到3个小正方形,则一共看到(4+5+3)个小正方形;
根据正方形的面积=边长×边长,求出一个面的面积,再乘从前面、上面和左面看到小正方形的个数即可。
【详解】1×1=1(cm2)
1×(4+5+3)
=1×12
=12(cm2)
如果从前面、上面和左面看,所看到的图形面积之和是12cm2。
【点睛】本题考查从不同方向观察立体图形,从前面、上面、左面这三个方向正确数出看到的小正方形的个数是解题的关键。
10. 5 7
【分析】从上面看到的图形可得,这个图形底层前面一行1个小正方体,后面一行3个正方体,所以至少有4个小正方体;
从左面看到的图形可得,前面一行只有1层,所以前面一行只有1个正方形,后面一行是2层,要使小正方体最少,则上层只有1个正方体;要使小正方体最多,则上层是3个正方体。
【详解】最少有:4+1=5(个)
最多有:4+3=7(个)
搭这样的立体图形,最少需要5个小正方体,最多可以有7个小正方体。
11.A
【分析】A.从上面看有2行,下边1行3个小正方形,上边1行靠右1个小正方形;从前面看有2行,下边1行3个小正方形,上边1行靠右1个小正方形;
B.从上面看有2行,上边1行3个小正方形,下边1行靠右1个小正方形;从前面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;
C.从上面看有2行,上边1行3个小正方形,下边1行中间1个小正方形;从前面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;
D.从上面看是1行3个小正方形;从前面看有2行,下边1行3个小正方形,上边1行中间1个小正方形。
【详解】
A.从上面看到的图形是,从前面看到的图形是;
B.从上面看到的图形是,从前面看到的图形是;
C.从上面看到的图形是,从前面看到的图形是;
D.从上面看到的图形是,从前面看到的图形是。
从上面和前面看到的图形相同的是,都是。
故答案为:A
12.C
【分析】根据从左面看的图形,可知立体图形有三行两层;根据从正面看的图形,可知立体图形有三列两层;综合以上,则第二行第二列处必须上下重叠摆放2个小正方体,据此试着拼摆这个立体图形,并数出最多需要几个小正方体即可。
【详解】符合从左面、正面看到的图形,最少需要的小正方体块数如图1所示,最多需要的小正方体块数如图2所示,所以要搭成这样的几何体最多需要10个小正方体。
故答案为:C
13.C
【分析】
根据从上面看到的形状和数字,可以确定这个几何体如图,从左面看有3行,下边1行3个小正方形;中间1行2个小正方形,左对齐;上边1行1个小正方形,居中;据此分析。
【详解】
根据分析,这个几何体从左面看是。
故答案为:C
14.C
【分析】A.从正面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;从上面看有2列,右边1列3个小正方形,左边1列靠上1个小正方形;从右面看有2行,下边1行3个小正方形,上边1行靠右1个小正方形;
B.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;
C.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,上边1行3个小正方形,下边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形;
D.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,上边1行3个小正方形,下边1行靠左1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形。
【详解】
A.从正面看是,从上面看是,从右面看是;
B.从正面看是,从上面看是,从右面看是;
C.从正面看是,从上面看是,从右面看是;
D.从正面看是,从上面看是,从右面看是。
用5个正方体搭成一个几何体,从正面看是,从上面看是,从右面看是,这个几何体是。
故答案为:C
15.B
【分析】从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从左面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;从上面看有2行,前边1行3个小正方形,后边1行靠右1个小正方形。
【详解】
从正面看到的是,从左面看到的是,从上面看到的是。
不可能看到的图案是。
故答案为:B
16.B
【分析】根据从上面看到的形状,可以确定底层有4个小正方体,以及这4个小正方体的摆放位置;根据从左面看到的形状,可以确定第二层的1个小正方体只能摆到并排的3个小正方体的上面,据此分析。
【详解】
如图,一共有3种不同的摆法。
故答案为:B
17.见详解
【分析】观察图形可知,从上面看到的是2层:上层3个正方形,下层1个正方形靠右边;从正面看到的是2层:下层3个正方形,上层1个正方形靠右边;从左面看到的图形是2层:下层2个正方形,上层1个正方形靠左边。
【详解】
18.作图见详解;5
【分析】根据从正面、左面、上面看到的形状,确定几何体如图,右面看到的图形与左面看到的图形左右相反,据此画出右面看到的图形,数出小正方体数量即可。
【详解】从右面看是,这个几何体有5个小正方体组成。
【点睛】观察一个用小正方体搭建的立方体图形,发现从不同的位置观察到图形的形状可能是不同的。
19.;;
【详解】用5个同样的小正方体摆成的立林图形,有3种拼法:
所以从正面看到的分别是;;。
答:从正面看到的分别是;; 。
【点睛】此题可以把从不同方向看到的平面图形进行综合分析,从而确定立体图形的形状。
20.(1)5
(2)见详解
【分析】(1)观察几何体,用小正方体摆了2层,底层4个小正方体,上层1个小正方体,共5个小正方体组成;
(2)从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,前边1行3个小正方形,后边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形。
【详解】(1)观察可知,上图是由5个小正方体组成的。
(2)
21.最少需要6个小正方体,最多可以有9个小正方体。
【解析】略
22.8个
【分析】由主视图,我们可以观察到行数最多为3行,列数最多为3列,由左到右,货箱个数呈2、1、3排列;接着看俯视图,共有2行,其中排在靠前一行只有一个货箱,位于右下角,结合主视图,我们基本可以确定,刚才呈2、1排列的货箱位于靠后一行,至于那竖直的3个货箱,要结合左视图确定;从左面看,共有2列,第1列竖直2个,第2列竖直3个。至此我们可以总结出:从左面看第1列的2个决定了组合体后一排最高只有2个,前排最高只有3个,而且最后一排左边最多有2个,中间1个,右边最多有2个。
【详解】 2+1+2+3=8(个)
答:这堆正方体货箱最多有8个。
【点睛】本题难度较大,需要一边观察三视图,一边想象立体图形的样子。在反复试验中一步步确定货箱的个数。并且题目给的三视图确定的几何体并不唯一,我们所求的是最多的那一种。
23.9块
【分析】由从上向下看到的视图易得最底层小正方体的个数,由从正面看到的视图和从左向右看到的视图找到其余层数里小正方体的个数相加即可。
【详解】如图:
由从上向下看到的视图易得最底层有6个小正方体,第二层最多也有2个小正方体,第二层最多也有1个小正方体,
所以这堆木块最多共有
6+2+1
=8+1
=9(块)
答:这堆木块共有9块。
【点睛】考查了从不同方向观察物体和几何体,解答此题应注意从上向下看到的视图决定底层正方体的个数。
24.见详解
【分析】
无论用4个、5个、6个、7个或更多的小正方体组成的几何体,从前面看到的形状都是,只要满足这个条件即可。
【详解】(1)这个几何体如果是由4个小正方体组成的,可以这样摆,如图:
(答案不唯一)
(2)这个几何体如果是由5个、6个、7个小正方体或更多的小正方体组成的,可以这样摆,如图:
(答案不唯一)
25.(1)20个
(2)5
【分析】从下往上一层一层数,然后加起来即可;第一层:10个,第二层:1+2+3=6(个),第三层:1+2=3(个),第四层:1个,一共10+6+3+1=10(个),据此解答;
(2)从图中取走1个小正方体后,从正面、上面、右面看到的图形不变,那么这个小正方体必须有3面,即后面、下面、左面都与其他正方体接触,这样拿走它从正面、上面、右面看到的图形不变,所以这个小正方体是5号。
【详解】由分析可知:
(1)10+(1+2+3)+(1+2)+1
=10+6+3+1
=16+3+1
=20(个)
答:这个几何体一共有20个小正方体。
(2)从图中取走5号小正方体后,从正面、上面、右面看到的图形不变。
26.(1)④⑤;①③;④
(2)5
【分析】(1)从正面看到的是二行,最下面一行三个小正方形并排,上面一行一个放在中间;从侧面看是一列两个,上下排列;从上面看是二行三列,上下行各两个正方形,呈“Z”型排列。由此分析判断。
(2)几何体⑥从正面看到的形状如右: ,根据此图,展开想象,确定物体的形状。
【详解】
(1)从正面看到的是的有(④⑤),从侧面看到的是的有(①③),从上面看到的是的有(④)。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,可以有如下摆法。
共有5种。
【点睛】掌握物体三视体的画法及根据物体三视图确定物体的形状是解答的关键。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
