7.5 正态分布 课件(共25张PPT)
文档属性
| 名称 | 7.5 正态分布 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 10:51:55 | ||
图片预览







文档简介
(共25张PPT)
第七章 随机变量及其分布
7.5 正态分布
1.通过误差模型,知道服从正态分布的随机变量是连续型.
2.通过具体实例等,了解正态分布的特征.
3.识别参数对密度曲线的影响,并能解决简单的实际问题.
1. 两点分布:
X 0 1
P 1-p p
2. 二项分布:
X 0 1 … k … n
P … …
3. 超几何分布:
X 0 1 … k … n
P … …
离散型随机变量
复习回顾
生活中还有许多随机变量不是离散型的随机变量,例如:
连续型随机变量:
如果随机变量X的所有取值不可以逐个列举出来,而是充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类变量为连续型随机变量。
它的概率分布规律用什么来描述?
复习回顾
①小明上学途中等公交车的时间X;
②小麦的株高、穗长、单位面积产量,
③实验中测量某零件尺寸的误差Y;
某市5月份的降雨量Z;
④某电器的使用寿命 ;
...
你还能举出几个这样的例子吗?
25.39 25.36 25.34 25.42 25.45 25.38 25.39 25.42
25.47 25.35 25.41 25.43 25.44 25.48 25.45 25.43
25.46 25.40 25.51 25.45 25.40 25.39 25.41 25.36
25.38 25.31 25.56 25.43 25.40 25.38 25.37 25.44
25.33 25.46 25.40 25.49 25.34 25.42 25.50 25.37
25.35 25.32 25.45 25.40 25.27 25.43 25.54 25.39
25.45 25.43 25.40 25.43 25.44 25.41 25.53 25.37
25.38 25.24 25.44 25.40 25.36 25.42 25.39 25.46
25.38 25.35 25.31 25.34 25.40 25.36 25.41 25.32
25.38 25.42 25.40 25.33 25.37 25.41 25.49 25.35
25.47 25.34 25.30 25.39 25.36 25.46 25.29 25.40
25.37 25.33 25.40 25.35 25.41 25.37 25.47 25.39
25.42 25.47 25.38 25.39
1.某钢铁加工厂生产内径为25.40mm的钢管,为了检验产品的质量,从一批产品中任取100件检测,用X表示它们的实际尺寸,测得X的值如下:
如何描述这100个样本数据的分布
分组 频数 频率 频率/组距
25.235~25.265 1 0.01 0.33
25.265~25.295 2 0.02 0.67
25.295~25.325 5 0.05 1.67
25.325~25.355 12 0.12 4
25.355~25.385 18 0.18 6
25.385~25.415 25 0.25 8.33
25.415~25.445 16 0.16 5.33
25.445~25.475 13 0.13 4.33
25.475~25.505 4 0.04 1.33
25.505~25.535 2 0.02 0.67
25.535~25.565 2 0.02 0.67
合计 100 1.00
频 率 分 布 表
产品尺寸
(mm)
频率
组距
25.235
25.295
25.355
25.415
25.475
25.535
25.265
25.325
25.385
25.445
25.505
25.565
2
4
6
8
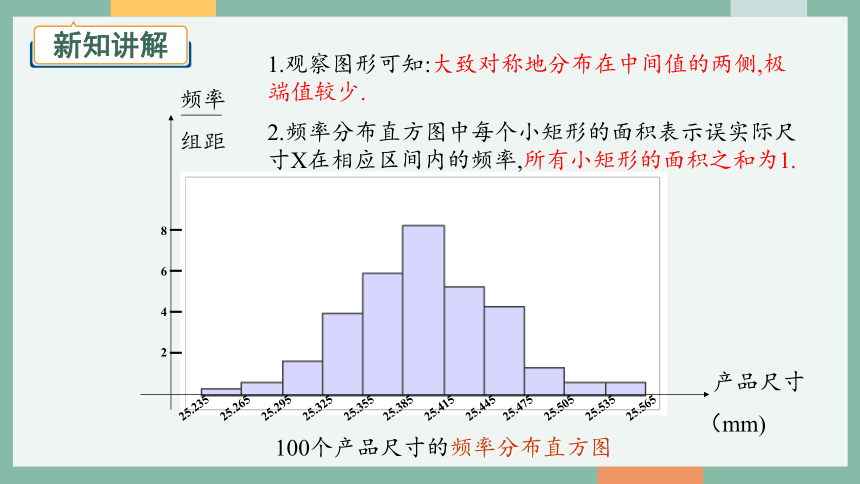
100个产品尺寸的频率分布直方图
2.频率分布直方图中每个小矩形的面积表示误实际尺寸X在相应区间内的频率,所有小矩形的面积之和为1.
1.观察图形可知:大致对称地分布在中间值的两侧,极端值较少.
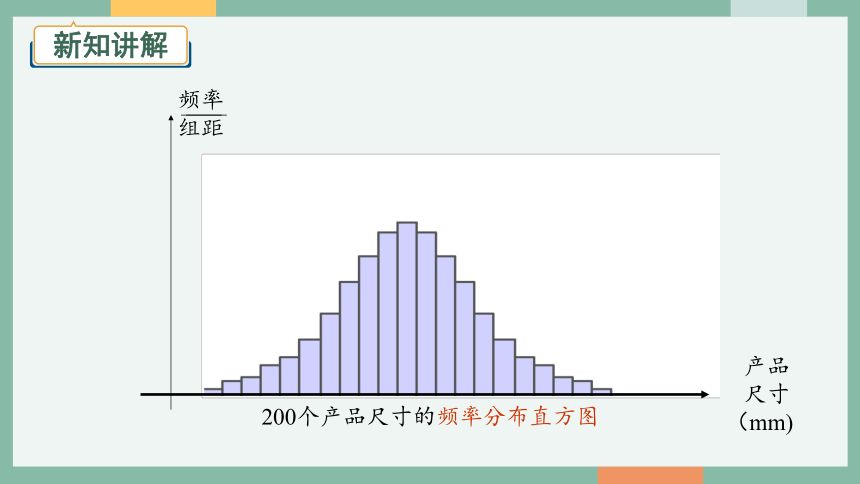
200个产品尺寸的频率分布直方图
频率
组距
产品
尺寸
(mm)
正态密度曲线
产品 尺寸
(mm)
频率
组距
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线.
曲线与水平轴之间的面积为1
x
y
函数
称为正态密度函数.
式中的 μ、σ (σ>0) 是参数,分别表示总体的平均数与标准差.
称它的图象是正态密度曲线.简称正态曲线.
知识归纳
若随机变量X的概率分布密度函数为
则称随机变量X 服从正态分布,记为X~N(μ,2).
正态曲线的性质 :
且对称区域面积相等;
具有两头低、中间高、左右对称的基本特征.
(5)当 无限增大时,曲线无限接近x轴.
(1)曲线位于轴的上方与轴不相交;
(2)曲线是单峰的,关于直线=μ对称;
(3)曲线在=μ处达到峰值
(4)曲线与轴之间的面积为1;
正态曲线的性质 :
σ越大,表示总体的分布越分散;
σ越小,表示总体的分布越集中.
μ=-1
μ=0
μ=1
σ=1
μ=0
=0.5
=1
=2
(5)参数μ定位置,σ定形状:
①当σ一定时,曲线随μ的变化沿轴平行移动;
②当μ一定时,σ越小越“瘦高”,σ越大越“矮胖”
正态函数表示式:
当 μ= 0,σ=1时,可得标准正态函数表示式:
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
标准正态曲线
标准正态曲线:
在实际遇到的许多随机现象都服从或近似服从正态分布:
在生产中,各种产品的质量指标;
在测量中,各种测量结果;
在生物学中,同一群体的某一特征如身高、体重等……;
在气象中,某地每年七月份的平均气温、平均湿度、
以及降雨量、水位等;
【答案】A
1. 设两个正态分布N(μ1,σ12)和N(μ2,σ22)(σ2>0)的密度函数图像如图,则有( )
A. μ1< μ2 , σ1<σ2 B. μ1< μ2 , σ1>σ2
A. μ1> μ2 , σ1<σ2 B. μ1>μ2 , σ1>σ2
小试牛刀
【答案】C
小试牛刀
2.若随机变量X服从正态分布,其正态曲线上的最高点的坐标是(10,),则该随机变量的方差等于( )
(A)10 (B)100 (C)(D)
正态曲线在特殊区间上的概率:
正态总体在 以外取值的概率只有 0.27 % , 通常
认为这种情况在一次试验中几乎不可能发生,称为小概率事件.
在实际应用中,通常认为服从于正态分布 x~N(μ,2) 的随机变量X只取 中的值,这在统计学中称为3原则.
例1 在某次考试中,考生的成绩X服从正态分布,即 X~N(90,100)
(1)求考试成绩X位于区间(70,110]上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]
之间的考生大约有多少人?
[解] ∵X~N(90,100),∴μ=90,σ=10.
(1)在该正态分布中,μ-2σ=70,μ+2σ=110,
∵P(μ-2σ∴考试成绩X位于区间(70,110]内的概率为0.9545.
例题讲解
例1 在某次考试中,考生的成绩X服从正态分布,即 X~N(90,100)
(1)求考试成绩X位于区间(70,110]上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]
之间的考生大约有多少人?
(2)μ-σ=80,μ+σ=100,
∵P(μ-σ∴考试成绩X位于区间(80,100]内的概率为0.6827.
由共有2000名考生,知考试成绩在(80,100]间的考生大约有2000×0.6827≈1 365(人).
例题讲解
例2 若X~N(5,1),求P(6解: 因为X~N(5,1),
故正态密度曲线关于直线 x=5 对称,
例题讲解
1).若X~N(μ,σ2),问X位于区域(μ,μ+σ)内的概率是多少?
解:由正态曲线的对称性可得,
小试牛刀
2).设随机变量(0,1),则P(≤1)=______,
P(≤1)=______,P(>1)=______.
3).已知(1, ),若P(<4)=0.9,则P(-2<<1)=( )
A.0.2 B.0.3 C.0.4 D.0.6
1. 正态曲线及正态密度函数
2. 正态分布:
3. 正态曲线的性质
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
(3)当|x|无限增大时,曲线无限接近x轴.
4. 正态分布的3σ原则
第七章 随机变量及其分布
7.5 正态分布
1.通过误差模型,知道服从正态分布的随机变量是连续型.
2.通过具体实例等,了解正态分布的特征.
3.识别参数对密度曲线的影响,并能解决简单的实际问题.
1. 两点分布:
X 0 1
P 1-p p
2. 二项分布:
X 0 1 … k … n
P … …
3. 超几何分布:
X 0 1 … k … n
P … …
离散型随机变量
复习回顾
生活中还有许多随机变量不是离散型的随机变量,例如:
连续型随机变量:
如果随机变量X的所有取值不可以逐个列举出来,而是充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类变量为连续型随机变量。
它的概率分布规律用什么来描述?
复习回顾
①小明上学途中等公交车的时间X;
②小麦的株高、穗长、单位面积产量,
③实验中测量某零件尺寸的误差Y;
某市5月份的降雨量Z;
④某电器的使用寿命 ;
...
你还能举出几个这样的例子吗?
25.39 25.36 25.34 25.42 25.45 25.38 25.39 25.42
25.47 25.35 25.41 25.43 25.44 25.48 25.45 25.43
25.46 25.40 25.51 25.45 25.40 25.39 25.41 25.36
25.38 25.31 25.56 25.43 25.40 25.38 25.37 25.44
25.33 25.46 25.40 25.49 25.34 25.42 25.50 25.37
25.35 25.32 25.45 25.40 25.27 25.43 25.54 25.39
25.45 25.43 25.40 25.43 25.44 25.41 25.53 25.37
25.38 25.24 25.44 25.40 25.36 25.42 25.39 25.46
25.38 25.35 25.31 25.34 25.40 25.36 25.41 25.32
25.38 25.42 25.40 25.33 25.37 25.41 25.49 25.35
25.47 25.34 25.30 25.39 25.36 25.46 25.29 25.40
25.37 25.33 25.40 25.35 25.41 25.37 25.47 25.39
25.42 25.47 25.38 25.39
1.某钢铁加工厂生产内径为25.40mm的钢管,为了检验产品的质量,从一批产品中任取100件检测,用X表示它们的实际尺寸,测得X的值如下:
如何描述这100个样本数据的分布
分组 频数 频率 频率/组距
25.235~25.265 1 0.01 0.33
25.265~25.295 2 0.02 0.67
25.295~25.325 5 0.05 1.67
25.325~25.355 12 0.12 4
25.355~25.385 18 0.18 6
25.385~25.415 25 0.25 8.33
25.415~25.445 16 0.16 5.33
25.445~25.475 13 0.13 4.33
25.475~25.505 4 0.04 1.33
25.505~25.535 2 0.02 0.67
25.535~25.565 2 0.02 0.67
合计 100 1.00
频 率 分 布 表
产品尺寸
(mm)
频率
组距
25.235
25.295
25.355
25.415
25.475
25.535
25.265
25.325
25.385
25.445
25.505
25.565
2
4
6
8
100个产品尺寸的频率分布直方图
2.频率分布直方图中每个小矩形的面积表示误实际尺寸X在相应区间内的频率,所有小矩形的面积之和为1.
1.观察图形可知:大致对称地分布在中间值的两侧,极端值较少.
200个产品尺寸的频率分布直方图
频率
组距
产品
尺寸
(mm)
正态密度曲线
产品 尺寸
(mm)
频率
组距
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线.
曲线与水平轴之间的面积为1
x
y
函数
称为正态密度函数.
式中的 μ、σ (σ>0) 是参数,分别表示总体的平均数与标准差.
称它的图象是正态密度曲线.简称正态曲线.
知识归纳
若随机变量X的概率分布密度函数为
则称随机变量X 服从正态分布,记为X~N(μ,2).
正态曲线的性质 :
且对称区域面积相等;
具有两头低、中间高、左右对称的基本特征.
(5)当 无限增大时,曲线无限接近x轴.
(1)曲线位于轴的上方与轴不相交;
(2)曲线是单峰的,关于直线=μ对称;
(3)曲线在=μ处达到峰值
(4)曲线与轴之间的面积为1;
正态曲线的性质 :
σ越大,表示总体的分布越分散;
σ越小,表示总体的分布越集中.
μ=-1
μ=0
μ=1
σ=1
μ=0
=0.5
=1
=2
(5)参数μ定位置,σ定形状:
①当σ一定时,曲线随μ的变化沿轴平行移动;
②当μ一定时,σ越小越“瘦高”,σ越大越“矮胖”
正态函数表示式:
当 μ= 0,σ=1时,可得标准正态函数表示式:
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
标准正态曲线
标准正态曲线:
在实际遇到的许多随机现象都服从或近似服从正态分布:
在生产中,各种产品的质量指标;
在测量中,各种测量结果;
在生物学中,同一群体的某一特征如身高、体重等……;
在气象中,某地每年七月份的平均气温、平均湿度、
以及降雨量、水位等;
【答案】A
1. 设两个正态分布N(μ1,σ12)和N(μ2,σ22)(σ2>0)的密度函数图像如图,则有( )
A. μ1< μ2 , σ1<σ2 B. μ1< μ2 , σ1>σ2
A. μ1> μ2 , σ1<σ2 B. μ1>μ2 , σ1>σ2
小试牛刀
【答案】C
小试牛刀
2.若随机变量X服从正态分布,其正态曲线上的最高点的坐标是(10,),则该随机变量的方差等于( )
(A)10 (B)100 (C)(D)
正态曲线在特殊区间上的概率:
正态总体在 以外取值的概率只有 0.27 % , 通常
认为这种情况在一次试验中几乎不可能发生,称为小概率事件.
在实际应用中,通常认为服从于正态分布 x~N(μ,2) 的随机变量X只取 中的值,这在统计学中称为3原则.
例1 在某次考试中,考生的成绩X服从正态分布,即 X~N(90,100)
(1)求考试成绩X位于区间(70,110]上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]
之间的考生大约有多少人?
[解] ∵X~N(90,100),∴μ=90,σ=10.
(1)在该正态分布中,μ-2σ=70,μ+2σ=110,
∵P(μ-2σ
例题讲解
例1 在某次考试中,考生的成绩X服从正态分布,即 X~N(90,100)
(1)求考试成绩X位于区间(70,110]上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]
之间的考生大约有多少人?
(2)μ-σ=80,μ+σ=100,
∵P(μ-σ
由共有2000名考生,知考试成绩在(80,100]间的考生大约有2000×0.6827≈1 365(人).
例题讲解
例2 若X~N(5,1),求P(6
故正态密度曲线关于直线 x=5 对称,
例题讲解
1).若X~N(μ,σ2),问X位于区域(μ,μ+σ)内的概率是多少?
解:由正态曲线的对称性可得,
小试牛刀
2).设随机变量(0,1),则P(≤1)=______,
P(≤1)=______,P(>1)=______.
3).已知(1, ),若P(<4)=0.9,则P(-2<<1)=( )
A.0.2 B.0.3 C.0.4 D.0.6
1. 正态曲线及正态密度函数
2. 正态分布:
3. 正态曲线的性质
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
(3)当|x|无限增大时,曲线无限接近x轴.
4. 正态分布的3σ原则
