7.5 正态分布 课件(共28张PPT)
文档属性
| 名称 | 7.5 正态分布 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 69.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
7.5 正态分布
1.通过误差模型,知道服从正态分布的随机变量是连续型.
2.通过具体实例等,了解正态分布的特征.
3.识别参数对密度曲线的影响,并能解决简单的实际问题.
正态曲线与正态分布的历史渊源
早在1734 年,法国数学家棣莫弗(A.DeMoivre,1667~1754)在研究二项概率的近似计算时,已提出了正态密度函数的形式,但当时只是作为一个数学表达式.
直到德国数学家高斯(C.F.Gauss,1777~1855)提出“正态误差"的理论后,正态密度函数才取得“概率分布”的身份.因此,人们也称正态分布为高斯分布.
法国数学家棣莫弗(1667~1754) 德国数学家高斯(1777~1855)
现实中,除了前面已经研究过的离散型随机变量外,还有大量问题中的随机变量不是离散型的,它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类随机变量为连续型随机变量.
离散型随机变量的概率分布规律用分布列描述:
两点分布、超几何分布、二项分布等
连续型随机变量的概率分布规律用什么来描述?
人的身高、体重、肺活量;电视机的寿命;小麦的株高、穗长、单位面积产量;零件的尺寸;某地每年7月的平均气温、降水量;居民的月均用水量……
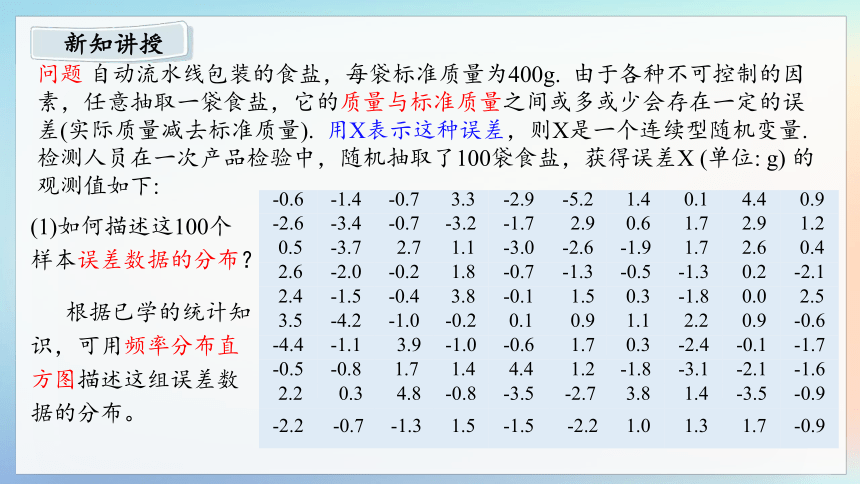
问题 自动流水线包装的食盐,每袋标准质量为400g. 由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差(实际质量减去标准质量). 用X表示这种误差,则X是一个连续型随机变量. 检测人员在一次产品检验中,随机抽取了100袋食盐,获得误差X (单位: g) 的观测值如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
(1)如何描述这100个样本误差数据的分布?
根据已学的统计知识,可用频率分布直方图描述这组误差数据的分布。
(1)求极差(即一组数据中最大值与最小值的差)
(2)决定组距与组数(将数据分组)
(3)将数据分组
画频率分布直方图的一般步骤为:
(4)列出频率分布表.(填写频率/组距一栏)
(5)画出频率分布直方图.
组距:指每个小组的两个端点的距离,
组数:将数据分组,当数据在100个以内时, 按数据多少常分5-12组.
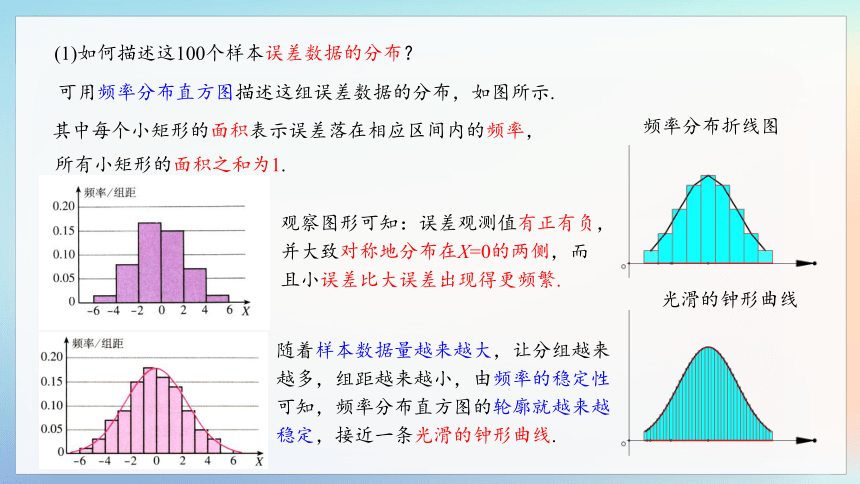
(1)如何描述这100个样本误差数据的分布?
可用频率分布直方图描述这组误差数据的分布,如图所示.
观察图形可知:误差观测值有正有负,并大致对称地分布在X=0的两侧,而且小误差比大误差出现得更频繁.
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线.
频率分布折线图
光滑的钟形曲线
其中每个小矩形的面积表示误差落在相应区间内的频率,
所有小矩形的面积之和为1.
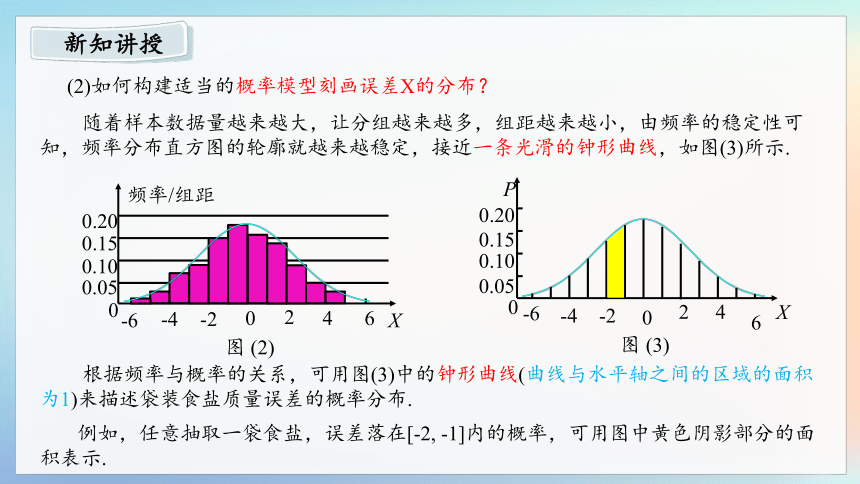
(2)如何构建适当的概率模型刻画误差X的分布?
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线,如图(3)所示.
频率/组距
X
-6
0
-4
-2
0
0.15
0.05
图 (2)
0.10
0.20
4
2
6
根据频率与概率的关系,可用图(3)中的钟形曲线(曲线与水平轴之间的区域的面积为1)来描述袋装食盐质量误差的概率分布.
例如,任意抽取一袋食盐,误差落在[-2, -1]内的概率,可用图中黄色阴影部分的面积表示.
P
X
-6
0
-4
-2
0
0.15
0.05
图 (3)
0.10
0.20
4
2
6
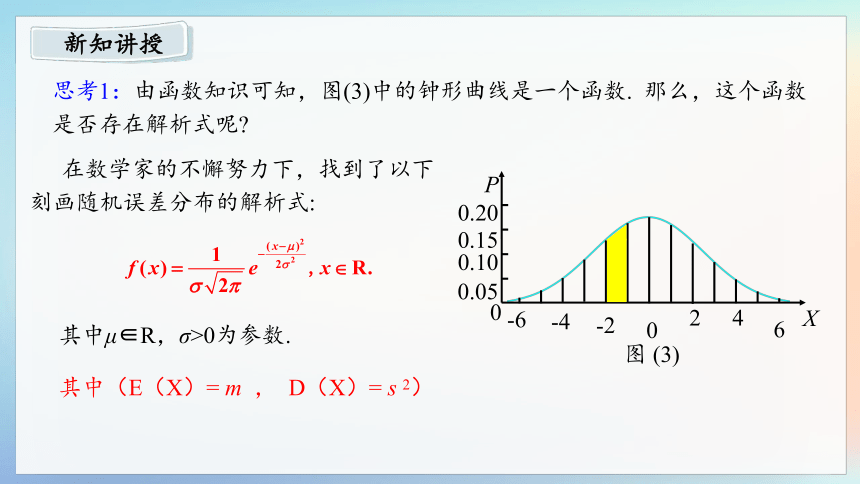
思考1:由函数知识可知,图(3)中的钟形曲线是一个函数. 那么,这个函数是否存在解析式呢
在数学家的不懈努力下,找到了以下刻画随机误差分布的解析式:
其中μ∈R,σ>0为参数.
其中(E(X)= m , D(X)= s 2)
P
X
-6
0
-4
-2
0
0.15
0.05
图 (3)
0.10
0.20
4
2
6
正态分布
P
X
-6
0
-4
-2
0
0.15
0.05
图 (3)
0.10
0.20
4
2
6
其中μ∈R,σ>0为参数.
显然,对任意的x∈R,f(x)>0,它的图象在x轴的上方,可以证明x轴和曲线之间的区域的面积为1.
特别地,当μ=0, σ=1时,称随机变量X
服从标准正态分布.
y
0
1
2
-1
-2
x
-3
3
μ=0
σ=1
我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线. 若随机变量X的概率分布密度函数为f(x),则称随机变量X
服从正态分布,记为X~N(μ, σ2).
100个数据(食盐质量误差)
100个数据的频率分布直方图轮廓
n(n>>100)个数据的频率分布直方图轮廓
接近一条光滑的钟型曲线
正态密度曲线
思考2:正态分布曲线是如何刻画随机变量的概率分布的呢?
若X~N(μ,σ2),则如右图所示,
面积即为概率!
X取值不超过x的概率P(X≤x)为图中区域A的面积,
而P(a≤X≤b)为区域B的面积.
f (x)
x
μ
a
A
图 (4)
B
x
b
O
思考3: 观察正态曲线及相应的密度函数,你能发现正态曲线的哪些特点
f (x)
x
μ
a
A
图 (4)
B
x
b
O
其中μ∈R,σ>0为参数.
由X的密度函数及图象可以发现,正态曲线有以下特点:
①曲线在轴上方,当||无限增大时,曲线无限接近x轴;
②曲线是单峰的,关于直线对称.
③曲线在处达到峰值为.
④曲线与轴间的区域面积为1 P(<)=P(≥)=0.5.
思考4:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形状有何影响 它们反映正态分布的哪些特征
(1).当参数取定值时,观察对正态分布的曲线。
3
1
2
σ=0.5
μ=-1
μ=0
μ=1
由于正态曲线关于x=μ对称,因此,当参数σ固定时,正态曲线的位置由μ确定,且随着μ的变化而沿x轴平移,
故μ称为位置参数
所以参数μ反映了正态分布的集中位置,可以用均值来估计,故有E(X)=μ.
(2)当参数取定值时,观察对正态曲线的影响
μ=0
=0.5
=1
=2
当μ固定时,因为正态曲线的峰值与σ成反比,而且对任意的σ>0,正态曲线与x轴之间的区域的面积总为1.
σ越大,曲线越“矮胖”,
表示总体的分布越分散;
σ越小,曲线越“瘦高”,
表示总体的分布越集中.
所以σ反映了随机变量的分布相对于均值μ的离散程度,可以用标准差来估计,故有D(X)=σ2.
故称为形状参数
思考4:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形状有何影响 它们反映正态分布的哪些特征
(1) 曲线在x轴的上方,与x轴不相交;
(3) 曲线与x轴之间的面积为1;
(4) 当μ一定时,σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5) 参数μ反映了正态分布的集中位置,σ反映了随机变量的分布相对于均值μ的离散程度.
在实际问题中,参数μ, σ可以分别用样本均值和样本标准差来估计,故有
(2) 曲线是单峰的,它关于直线x=μ对称,
且在x=μ处取得最大值 ;
f (x)
x
μ
a
A
B
x
b
O
正态曲线的性质:
归纳总结
1.如图所示,是一个正态曲线.试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的均值和方差.
例.李明上学有时坐公交车, 有时骑单车, 他各记录了50次坐公交车和骑单车所花的时间, 经数据分析得到: 坐公交车平均用时30min, 样本方差为36; 骑单车平均用时34min, 样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
解:(1)随机变量X的样本均值为30,样本标准差为6,
随机变量Y的样本均值为34,样本标准差为2,
用样本均值估计参数μ,用样本标准差估计参数σ,
可得X~N(30,62),Y~N(34,22).
例题讲解
例题讲解
例.李明上学有时坐公交车, 有时骑单车, 他各记录了50次坐公交车和骑单车所花的时间, 经数据分析得到: 坐公交车平均用时30min, 样本方差为36; 骑单车平均用时34min, 样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
X和Y的分布密度曲线绘图如下:
(1)X~N(30,62),Y~N(34,22).
若有38 min可用,则骑单车不迟到的概率大,应选择骑单车;
若只有34 min可用,则坐公交车不迟到的概率大,应选择坐公交车.
(3)应选择在给定时间内不迟到的概率大的交通工具.
由图知,P(X≤38)P(Y≤34).
例题讲解
例.李明上学有时坐公交车, 有时骑单车, 他各记录了50次坐公交车和骑单车所花的时间, 经数据分析得到: 坐公交车平均用时30min, 样本方差为36; 骑单车平均用时34min, 样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
正态曲线下的面积规律:
-x1 -x2 x2 x1
a
-a
正态曲线下对称区域的面积相等
对应的概率也相等
利用“对称法”求正态分布下随机变量在某个区间的概率
0
1
2
-1
-2
x
y
-3
3
4
μ=1
0.5
1-a
a
1-a
1-2a
1. 若X~N(2, 32),则E(X)=______,D(X)=_______.
2
9
3
2
2. X~N(μ, σ2),若E(X)=3, σ(X)=2,则μ=______, σ=______.
3.若X~N(1, σ2),且P(X<0)=a,则
(1) P(X>1)=_______;
(2) P(X>0)=______;
(3) P(X>2)=______;
(4) P(X<2)=______;
(5) P(0(6) P(00.5-a
正态分布在概率和统计中占有重要地位,它广泛存在于自然现象、生产和生活实践之中.
在现实生活中,很多随机变量都服从或近似服从正态分布.例如,某些物理量的测量误差,某一地区同年龄人群的身高、体重、肺活量等,一定条件下生长的小麦的株高、穗长、单位面积产量,自动流水线生产的各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容),某地每年7月的平均气温、平均湿度、降水量等,一般都近似服从正态分布.
正态曲线的应用
假设X~N(μ, σ2),可以证明: 对给定的k∈N*,P(μ-kσ≤X≤μ+kσ)是一个只与k有关的定值.
由此看到,尽管正态变量的取值范围是(-∞, +∞),但在一次试验中,X的取值几乎总是落在区间[μ-3σ, μ+3σ]内,而在此区间以外取值的概率大约只有0.0027,通常认为这种情况几乎不可能发生.
在实际应用中, 通常认为服从于正态分布N(μ, σ2)的随机变量X只取[μ-3σ, μ+3σ]中的值, 这在统计学中称为3σ原则.
3σ原则
1.设随机变量X~N(0,1),则X的密度函数为_______________,
P(X≤0)=_________,P(|X|≤1)=________,
P(X<1)=_________,P(X>1)=________.(精确到0.0001.)
0.5
0.6827
0.8414
0.1586
方法:把普通的待求区间向(μ σ,μ+σ),(μ 2σ,μ+2σ),(μ 3σ,μ+3σ)这三个区间进行转化,然后利用3个特殊概率、0.5、1等求出相应概率.
正态曲线和3σ原则的应用
(1)利用正态密度曲线的对称性研究相关概率问题,涉及的知识主要是正态曲线关于直线x=μ对称,曲线与x轴之间的区域的面积为1.
(2)利用3σ原则求概率问题时,要注意把给出的区间或范围与μ, σ进行对比联系,确定它们属于[μ-σ, μ+σ],[μ-2σ, μ+2σ],[μ-3σ, μ+3σ]中的哪一个.
正态分布下两类常见的概率计算
归纳总结
2.某市高二年级男生的身高X(单位:cm)近似服从正态分布N(170,5 ),随机选择一名本市高二年级的男生,求下列事件的概率:
(1)P(165(2)P(X≤165)=__________
(3)P(X>175)=__________
0.6827
0.15865
0.15865
3.袋装食盐标准质量为400g,规定误差的绝对值不超过4g就认为合格.假设误差服从正态分布,随机抽取100袋食盐,误差的样本均值为0,样本方差为4,请你估计这批袋装食盐的合格率.
解:误差X~N(0,2 ),则食盐的合格率为P(≤4)=P(-4≤X≤4)=95.45%
若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记为X~N(μ, σ2). 特别地,当μ=0, σ=1时,称随机变量X服从标准正态分布.
1. 正态分布:
正态密度函数:
2.特殊区间的概率:
7.5 正态分布
1.通过误差模型,知道服从正态分布的随机变量是连续型.
2.通过具体实例等,了解正态分布的特征.
3.识别参数对密度曲线的影响,并能解决简单的实际问题.
正态曲线与正态分布的历史渊源
早在1734 年,法国数学家棣莫弗(A.DeMoivre,1667~1754)在研究二项概率的近似计算时,已提出了正态密度函数的形式,但当时只是作为一个数学表达式.
直到德国数学家高斯(C.F.Gauss,1777~1855)提出“正态误差"的理论后,正态密度函数才取得“概率分布”的身份.因此,人们也称正态分布为高斯分布.
法国数学家棣莫弗(1667~1754) 德国数学家高斯(1777~1855)
现实中,除了前面已经研究过的离散型随机变量外,还有大量问题中的随机变量不是离散型的,它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类随机变量为连续型随机变量.
离散型随机变量的概率分布规律用分布列描述:
两点分布、超几何分布、二项分布等
连续型随机变量的概率分布规律用什么来描述?
人的身高、体重、肺活量;电视机的寿命;小麦的株高、穗长、单位面积产量;零件的尺寸;某地每年7月的平均气温、降水量;居民的月均用水量……
问题 自动流水线包装的食盐,每袋标准质量为400g. 由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间或多或少会存在一定的误差(实际质量减去标准质量). 用X表示这种误差,则X是一个连续型随机变量. 检测人员在一次产品检验中,随机抽取了100袋食盐,获得误差X (单位: g) 的观测值如下:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
2.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
(1)如何描述这100个样本误差数据的分布?
根据已学的统计知识,可用频率分布直方图描述这组误差数据的分布。
(1)求极差(即一组数据中最大值与最小值的差)
(2)决定组距与组数(将数据分组)
(3)将数据分组
画频率分布直方图的一般步骤为:
(4)列出频率分布表.(填写频率/组距一栏)
(5)画出频率分布直方图.
组距:指每个小组的两个端点的距离,
组数:将数据分组,当数据在100个以内时, 按数据多少常分5-12组.
(1)如何描述这100个样本误差数据的分布?
可用频率分布直方图描述这组误差数据的分布,如图所示.
观察图形可知:误差观测值有正有负,并大致对称地分布在X=0的两侧,而且小误差比大误差出现得更频繁.
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线.
频率分布折线图
光滑的钟形曲线
其中每个小矩形的面积表示误差落在相应区间内的频率,
所有小矩形的面积之和为1.
(2)如何构建适当的概率模型刻画误差X的分布?
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线,如图(3)所示.
频率/组距
X
-6
0
-4
-2
0
0.15
0.05
图 (2)
0.10
0.20
4
2
6
根据频率与概率的关系,可用图(3)中的钟形曲线(曲线与水平轴之间的区域的面积为1)来描述袋装食盐质量误差的概率分布.
例如,任意抽取一袋食盐,误差落在[-2, -1]内的概率,可用图中黄色阴影部分的面积表示.
P
X
-6
0
-4
-2
0
0.15
0.05
图 (3)
0.10
0.20
4
2
6
思考1:由函数知识可知,图(3)中的钟形曲线是一个函数. 那么,这个函数是否存在解析式呢
在数学家的不懈努力下,找到了以下刻画随机误差分布的解析式:
其中μ∈R,σ>0为参数.
其中(E(X)= m , D(X)= s 2)
P
X
-6
0
-4
-2
0
0.15
0.05
图 (3)
0.10
0.20
4
2
6
正态分布
P
X
-6
0
-4
-2
0
0.15
0.05
图 (3)
0.10
0.20
4
2
6
其中μ∈R,σ>0为参数.
显然,对任意的x∈R,f(x)>0,它的图象在x轴的上方,可以证明x轴和曲线之间的区域的面积为1.
特别地,当μ=0, σ=1时,称随机变量X
服从标准正态分布.
y
0
1
2
-1
-2
x
-3
3
μ=0
σ=1
我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线. 若随机变量X的概率分布密度函数为f(x),则称随机变量X
服从正态分布,记为X~N(μ, σ2).
100个数据(食盐质量误差)
100个数据的频率分布直方图轮廓
n(n>>100)个数据的频率分布直方图轮廓
接近一条光滑的钟型曲线
正态密度曲线
思考2:正态分布曲线是如何刻画随机变量的概率分布的呢?
若X~N(μ,σ2),则如右图所示,
面积即为概率!
X取值不超过x的概率P(X≤x)为图中区域A的面积,
而P(a≤X≤b)为区域B的面积.
f (x)
x
μ
a
A
图 (4)
B
x
b
O
思考3: 观察正态曲线及相应的密度函数,你能发现正态曲线的哪些特点
f (x)
x
μ
a
A
图 (4)
B
x
b
O
其中μ∈R,σ>0为参数.
由X的密度函数及图象可以发现,正态曲线有以下特点:
①曲线在轴上方,当||无限增大时,曲线无限接近x轴;
②曲线是单峰的,关于直线对称.
③曲线在处达到峰值为.
④曲线与轴间的区域面积为1 P(<)=P(≥)=0.5.
思考4:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形状有何影响 它们反映正态分布的哪些特征
(1).当参数取定值时,观察对正态分布的曲线。
3
1
2
σ=0.5
μ=-1
μ=0
μ=1
由于正态曲线关于x=μ对称,因此,当参数σ固定时,正态曲线的位置由μ确定,且随着μ的变化而沿x轴平移,
故μ称为位置参数
所以参数μ反映了正态分布的集中位置,可以用均值来估计,故有E(X)=μ.
(2)当参数取定值时,观察对正态曲线的影响
μ=0
=0.5
=1
=2
当μ固定时,因为正态曲线的峰值与σ成反比,而且对任意的σ>0,正态曲线与x轴之间的区域的面积总为1.
σ越大,曲线越“矮胖”,
表示总体的分布越分散;
σ越小,曲线越“瘦高”,
表示总体的分布越集中.
所以σ反映了随机变量的分布相对于均值μ的离散程度,可以用标准差来估计,故有D(X)=σ2.
故称为形状参数
思考4:一个正态分布由参数μ和σ完全确定,这两个参数对正态曲线的形状有何影响 它们反映正态分布的哪些特征
(1) 曲线在x轴的上方,与x轴不相交;
(3) 曲线与x轴之间的面积为1;
(4) 当μ一定时,σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.
(5) 参数μ反映了正态分布的集中位置,σ反映了随机变量的分布相对于均值μ的离散程度.
在实际问题中,参数μ, σ可以分别用样本均值和样本标准差来估计,故有
(2) 曲线是单峰的,它关于直线x=μ对称,
且在x=μ处取得最大值 ;
f (x)
x
μ
a
A
B
x
b
O
正态曲线的性质:
归纳总结
1.如图所示,是一个正态曲线.试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的均值和方差.
例.李明上学有时坐公交车, 有时骑单车, 他各记录了50次坐公交车和骑单车所花的时间, 经数据分析得到: 坐公交车平均用时30min, 样本方差为36; 骑单车平均用时34min, 样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
解:(1)随机变量X的样本均值为30,样本标准差为6,
随机变量Y的样本均值为34,样本标准差为2,
用样本均值估计参数μ,用样本标准差估计参数σ,
可得X~N(30,62),Y~N(34,22).
例题讲解
例题讲解
例.李明上学有时坐公交车, 有时骑单车, 他各记录了50次坐公交车和骑单车所花的时间, 经数据分析得到: 坐公交车平均用时30min, 样本方差为36; 骑单车平均用时34min, 样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
X和Y的分布密度曲线绘图如下:
(1)X~N(30,62),Y~N(34,22).
若有38 min可用,则骑单车不迟到的概率大,应选择骑单车;
若只有34 min可用,则坐公交车不迟到的概率大,应选择坐公交车.
(3)应选择在给定时间内不迟到的概率大的交通工具.
由图知,P(X≤38)
例题讲解
例.李明上学有时坐公交车, 有时骑单车, 他各记录了50次坐公交车和骑单车所花的时间, 经数据分析得到: 坐公交车平均用时30min, 样本方差为36; 骑单车平均用时34min, 样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据(1)中的估计结果,利用信息技术工具画出X和Y的分布密度曲线;
正态曲线下的面积规律:
-x1 -x2 x2 x1
a
-a
正态曲线下对称区域的面积相等
对应的概率也相等
利用“对称法”求正态分布下随机变量在某个区间的概率
0
1
2
-1
-2
x
y
-3
3
4
μ=1
0.5
1-a
a
1-a
1-2a
1. 若X~N(2, 32),则E(X)=______,D(X)=_______.
2
9
3
2
2. X~N(μ, σ2),若E(X)=3, σ(X)=2,则μ=______, σ=______.
3.若X~N(1, σ2),且P(X<0)=a,则
(1) P(X>1)=_______;
(2) P(X>0)=______;
(3) P(X>2)=______;
(4) P(X<2)=______;
(5) P(0
正态分布在概率和统计中占有重要地位,它广泛存在于自然现象、生产和生活实践之中.
在现实生活中,很多随机变量都服从或近似服从正态分布.例如,某些物理量的测量误差,某一地区同年龄人群的身高、体重、肺活量等,一定条件下生长的小麦的株高、穗长、单位面积产量,自动流水线生产的各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容),某地每年7月的平均气温、平均湿度、降水量等,一般都近似服从正态分布.
正态曲线的应用
假设X~N(μ, σ2),可以证明: 对给定的k∈N*,P(μ-kσ≤X≤μ+kσ)是一个只与k有关的定值.
由此看到,尽管正态变量的取值范围是(-∞, +∞),但在一次试验中,X的取值几乎总是落在区间[μ-3σ, μ+3σ]内,而在此区间以外取值的概率大约只有0.0027,通常认为这种情况几乎不可能发生.
在实际应用中, 通常认为服从于正态分布N(μ, σ2)的随机变量X只取[μ-3σ, μ+3σ]中的值, 这在统计学中称为3σ原则.
3σ原则
1.设随机变量X~N(0,1),则X的密度函数为_______________,
P(X≤0)=_________,P(|X|≤1)=________,
P(X<1)=_________,P(X>1)=________.(精确到0.0001.)
0.5
0.6827
0.8414
0.1586
方法:把普通的待求区间向(μ σ,μ+σ),(μ 2σ,μ+2σ),(μ 3σ,μ+3σ)这三个区间进行转化,然后利用3个特殊概率、0.5、1等求出相应概率.
正态曲线和3σ原则的应用
(1)利用正态密度曲线的对称性研究相关概率问题,涉及的知识主要是正态曲线关于直线x=μ对称,曲线与x轴之间的区域的面积为1.
(2)利用3σ原则求概率问题时,要注意把给出的区间或范围与μ, σ进行对比联系,确定它们属于[μ-σ, μ+σ],[μ-2σ, μ+2σ],[μ-3σ, μ+3σ]中的哪一个.
正态分布下两类常见的概率计算
归纳总结
2.某市高二年级男生的身高X(单位:cm)近似服从正态分布N(170,5 ),随机选择一名本市高二年级的男生,求下列事件的概率:
(1)P(165
(3)P(X>175)=__________
0.6827
0.15865
0.15865
3.袋装食盐标准质量为400g,规定误差的绝对值不超过4g就认为合格.假设误差服从正态分布,随机抽取100袋食盐,误差的样本均值为0,样本方差为4,请你估计这批袋装食盐的合格率.
解:误差X~N(0,2 ),则食盐的合格率为P(≤4)=P(-4≤X≤4)=95.45%
若随机变量X的概率分布密度函数为f(x),则称随机变量X服从正态分布,记为X~N(μ, σ2). 特别地,当μ=0, σ=1时,称随机变量X服从标准正态分布.
1. 正态分布:
正态密度函数:
2.特殊区间的概率:
