4. 4利用三角形全等测距离 课件(共14张PPT)2024-2025学年北师大版数学七年级下册
文档属性
| 名称 | 4. 4利用三角形全等测距离 课件(共14张PPT)2024-2025学年北师大版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 166.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 18:36:39 | ||
图片预览




文档简介
(共14张PPT)
利用三角形全等测距离
第四章 三角形
4
探究与应用
课堂小结与检测
应用 利用三角形全等测距离
例 一位经历过战争的老人曾经讲述过这样
一个故事:在一次战役中,我军阵地与敌军碉
堡隔河相望(如图4-4-1).为了炸掉这个碉堡,
需要知道碉堡与我军阵地的距离.
探究与应用
图4-4-1
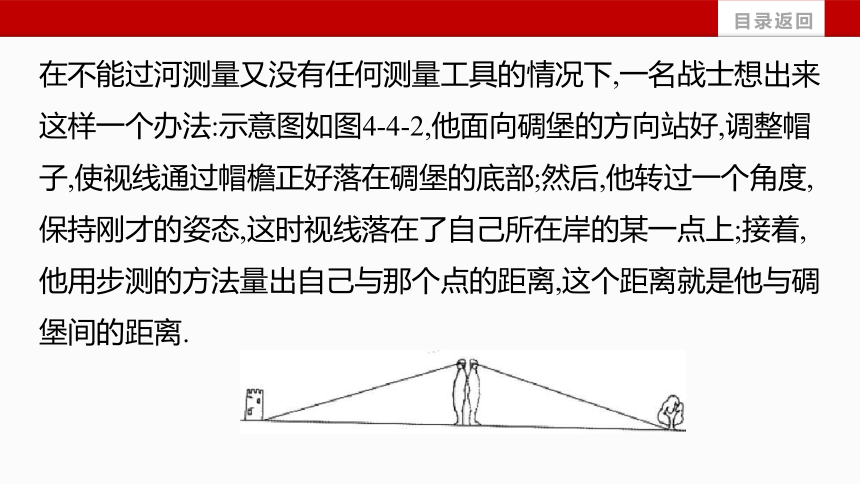
在不能过河测量又没有任何测量工具的情况下,一名战士想出来这样一个办法:示意图如图4-4-2,他面向碉堡的方向站好,调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上;接着,他用步测的方法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.
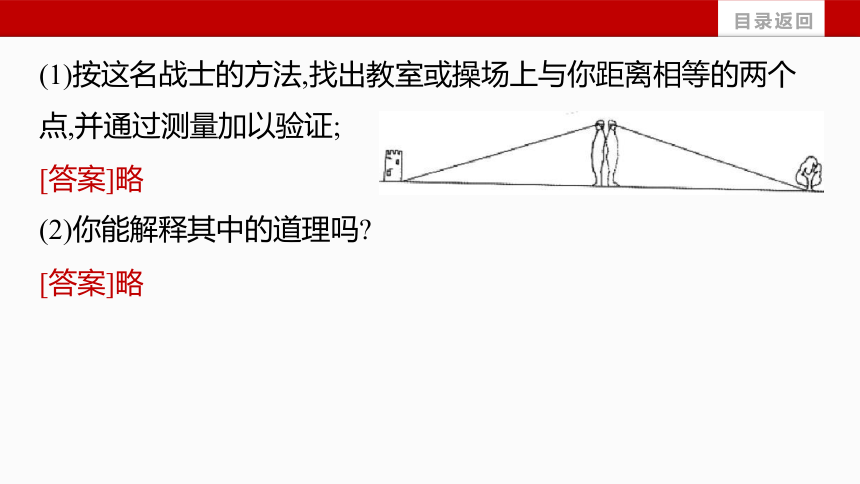
(1)按这名战士的方法,找出教室或操场上与你距离相等的两个点,并通过测量加以验证;
(2)你能解释其中的道理吗
[答案]略
[答案]略
利用三角形全等测距离
利用全等三角形测距离,通常依据“SAS或ASA”构造全等三角形,借助全等三角形的对应边相等,将不能直接测量的距离转化为可以直接测量的距离.
学 方法
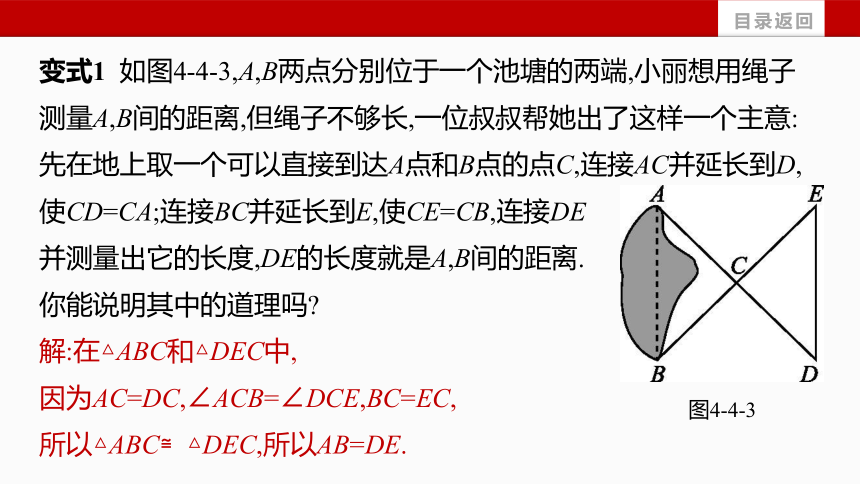
变式1 如图4-4-3,A,B两点分别位于一个池塘的两端,小丽想用绳子测量A,B间的距离,但绳子不够长,一位叔叔帮她出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE
并测量出它的长度,DE的长度就是A,B间的距离.
你能说明其中的道理吗
图4-4-3
解:在△ABC和△DEC中,
因为AC=DC,∠ACB=∠DCE,BC=EC,
所以△ABC≌△DEC,所以AB=DE.
变式2 阅读并完成相应的任务.
如下表中示意图,小华站在堤岸凉亭A点处,正对他的B点处停有一艘游艇,他想知道凉亭与这艘游艇之间的距离,于是制订了如下方案.
课题 测凉亭与游艇之间的距离
测量工具 皮尺等
测量方案 示意图 (不完整)
课题 测凉亭与游艇之间的距离
测量步骤 ①小华沿堤岸走到电线
杆C旁;
②再往前走相同的距离,
到达D点;
③然后他向左直行,当自己、电线杆与游艇在一条直线上时停下来,此时小华位于点E处
测量数据 AC=20米,CD=20米,DE=8米
任务一:根据题意将测量方案示意图补充完整.
解:任务一:将测量方案示意图补充完整如图.
D
E
任务二:(1)凉亭与游艇之间的距离是 米;
(2)请你说明小华的方案正确的理由.
8
(2)由题意可知,AC=20米,CD=20米,DE=8米,∠A=90°,∠D=90°,
所以AC=DC,∠A=∠D.
在△ABC和△DEC中,
因为∠A=∠D,AC=DC,∠ACB=∠DCE,
所以△ABC≌△DEC(ASA),
所以AB=DE=8米,所以小华的方案是正确的.
[检测]
1.如图4-4-4,为了测量出池塘两端A,B之间的距离,先在地面上取一点C,使∠ACB=90°,然后延长BC至点D,使CD=BC,连接AD,那么只要测量出AD的
长度就能得到A,B两点之间的距离,请说明其中的道理.
课堂小结与检测
图4-4-4
解:因为∠ACB=90°,所以∠ACB=∠ACD=90°.
在△ACD和△ACB中,因为AC=AC,∠ACD=∠ACB,CD=CB,
所以△ACD≌△ACB(SAS),所以AD=AB,
所以测量出AD的长度就能得到A,B两点之间的距离.
2.如图4-4-5,某湖泊岸边A,B两地有两棵大树,计划在两棵大树之间架一电话线路,为了计算两棵大树能承受的压力,需测量出A,B两地之间的距离,但是A,B两地又不能直接到达,请你用学过的知识设计一个测量方法,求出A,B两地之间的距离.
图4-4-5
解:方法不唯一,如图,在湖泊岸边找一点C,
连接AC,BC并延长,截取DC=BC,EC=AC,
连接DE.
在△ABC和△EDC中,因为BC=DC,∠ACB=∠ECD,AC=EC,
所以△ABC≌△EDC(SAS),所以AB=ED,
所以测量出ED的长即可得到A,B两地之间的距离.
C
E
D
利用三角形全等测距离
第四章 三角形
4
探究与应用
课堂小结与检测
应用 利用三角形全等测距离
例 一位经历过战争的老人曾经讲述过这样
一个故事:在一次战役中,我军阵地与敌军碉
堡隔河相望(如图4-4-1).为了炸掉这个碉堡,
需要知道碉堡与我军阵地的距离.
探究与应用
图4-4-1
在不能过河测量又没有任何测量工具的情况下,一名战士想出来这样一个办法:示意图如图4-4-2,他面向碉堡的方向站好,调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上;接着,他用步测的方法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.
(1)按这名战士的方法,找出教室或操场上与你距离相等的两个点,并通过测量加以验证;
(2)你能解释其中的道理吗
[答案]略
[答案]略
利用三角形全等测距离
利用全等三角形测距离,通常依据“SAS或ASA”构造全等三角形,借助全等三角形的对应边相等,将不能直接测量的距离转化为可以直接测量的距离.
学 方法
变式1 如图4-4-3,A,B两点分别位于一个池塘的两端,小丽想用绳子测量A,B间的距离,但绳子不够长,一位叔叔帮她出了这样一个主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB,连接DE
并测量出它的长度,DE的长度就是A,B间的距离.
你能说明其中的道理吗
图4-4-3
解:在△ABC和△DEC中,
因为AC=DC,∠ACB=∠DCE,BC=EC,
所以△ABC≌△DEC,所以AB=DE.
变式2 阅读并完成相应的任务.
如下表中示意图,小华站在堤岸凉亭A点处,正对他的B点处停有一艘游艇,他想知道凉亭与这艘游艇之间的距离,于是制订了如下方案.
课题 测凉亭与游艇之间的距离
测量工具 皮尺等
测量方案 示意图 (不完整)
课题 测凉亭与游艇之间的距离
测量步骤 ①小华沿堤岸走到电线
杆C旁;
②再往前走相同的距离,
到达D点;
③然后他向左直行,当自己、电线杆与游艇在一条直线上时停下来,此时小华位于点E处
测量数据 AC=20米,CD=20米,DE=8米
任务一:根据题意将测量方案示意图补充完整.
解:任务一:将测量方案示意图补充完整如图.
D
E
任务二:(1)凉亭与游艇之间的距离是 米;
(2)请你说明小华的方案正确的理由.
8
(2)由题意可知,AC=20米,CD=20米,DE=8米,∠A=90°,∠D=90°,
所以AC=DC,∠A=∠D.
在△ABC和△DEC中,
因为∠A=∠D,AC=DC,∠ACB=∠DCE,
所以△ABC≌△DEC(ASA),
所以AB=DE=8米,所以小华的方案是正确的.
[检测]
1.如图4-4-4,为了测量出池塘两端A,B之间的距离,先在地面上取一点C,使∠ACB=90°,然后延长BC至点D,使CD=BC,连接AD,那么只要测量出AD的
长度就能得到A,B两点之间的距离,请说明其中的道理.
课堂小结与检测
图4-4-4
解:因为∠ACB=90°,所以∠ACB=∠ACD=90°.
在△ACD和△ACB中,因为AC=AC,∠ACD=∠ACB,CD=CB,
所以△ACD≌△ACB(SAS),所以AD=AB,
所以测量出AD的长度就能得到A,B两点之间的距离.
2.如图4-4-5,某湖泊岸边A,B两地有两棵大树,计划在两棵大树之间架一电话线路,为了计算两棵大树能承受的压力,需测量出A,B两地之间的距离,但是A,B两地又不能直接到达,请你用学过的知识设计一个测量方法,求出A,B两地之间的距离.
图4-4-5
解:方法不唯一,如图,在湖泊岸边找一点C,
连接AC,BC并延长,截取DC=BC,EC=AC,
连接DE.
在△ABC和△EDC中,因为BC=DC,∠ACB=∠ECD,AC=EC,
所以△ABC≌△EDC(SAS),所以AB=ED,
所以测量出ED的长即可得到A,B两地之间的距离.
C
E
D
同课章节目录
