7.2 正弦、余弦(第2课时) 同步课件(共34张PPT)2024-2025学年九年级数学下册(苏科版)
文档属性
| 名称 | 7.2 正弦、余弦(第2课时) 同步课件(共34张PPT)2024-2025学年九年级数学下册(苏科版) |  | |
| 格式 | pptx | ||
| 文件大小 | 49.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 15:42:19 | ||
图片预览









文档简介
(共34张PPT)
7.2 正弦、余弦(2)
第2课时 用正弦、余弦解决问题
学习目标
1. 会利用直角三角形的三边关系求直角三角形中锐角的正弦、余弦值;
2.理解直角三角形中两个锐角的正弦、余弦之间的关系;
3.能利用三角函数解决简单的直角三角形问题.
知识回顾
如何表示直角三角形中一个锐角的正弦和余弦?
锐角的正弦值、余弦值随锐角的变化是如何变化的?
知识回顾
三
角
函
数
正弦
正切
余弦
sinA==
cosA==
tanA==
A
B
C
斜边c
对边a
邻边b
例1 如图,在Rt△ABC中,∠C=90°,AC=12,BC=5. 求sinA、cosA、sinB、cosB的值.
B
A
C
解:在Rt△ABC中,根据勾股定理,得
AB===13.
根据正弦、余弦的定义,得
sinA==,cosA==,
sinB==,cosB==.
例题讲解
观察与思考
在Rt△ABC(∠C=90°)中,sinA与cosB、cosA与sinB的值有什么关系
归纳与总结
∵ sinA== ,cosA== ,
sinB== ,cosB== .
∴ sinA=cosB, cosA=sinB.
A
B
C
斜边c
对边a
邻边b
在Rt△ABC中,若∠A+∠B=90°,则sinA=cosB,cosA=sinB.
例题讲解
例2 在Rt△ABC中,∠C=90°,如果sinA=,求cosA和tanA的值.
解:在Rt△ABC中,sinA=,
设BC=2a,则AB=3a,
根据勾股定理,得
AC== .
根据余弦、正切的定义,得
cosA===,tanA==.
拓展与延伸
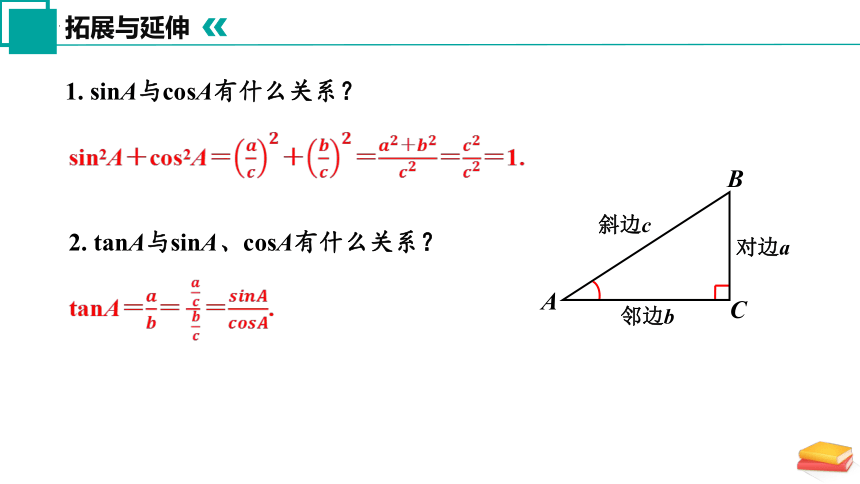
1. sinA与cosA有什么关系?
sin2A+cos2A=+===1.
2. tanA与sinA、cosA有什么关系?
tanA== =.
A
B
C
斜边c
对边a
邻边b
归纳与总结
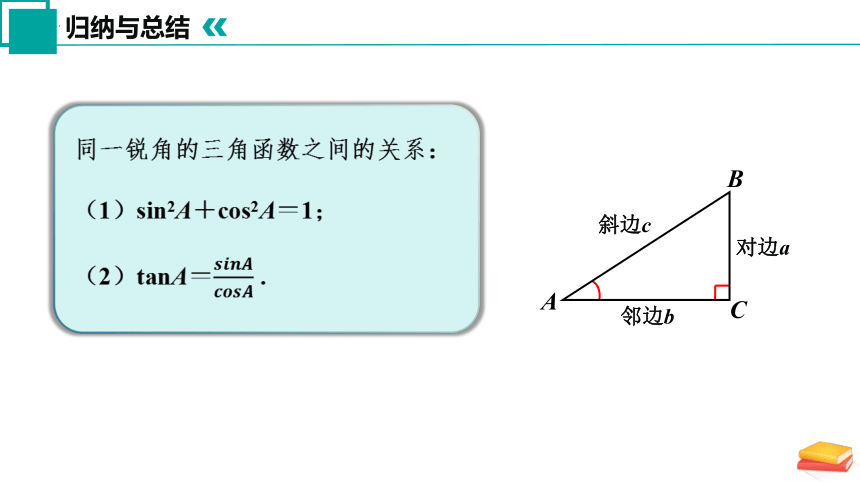
同一锐角的三角函数之间的关系:
(1)sin2A+cos2A=1;
(2)tanA= .
A
B
C
斜边c
对边a
邻边b
新知巩固
(1) sinα=,则cosα=____,tanα=____,
(2) cosα=,则sinα=____,tanα=____,
(3) tanα=,则sinα=____,cosα=____.
1. 已知α为锐角:
2. 如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,则sinB=______,cosB=____,tanB=____,sin2Bcos2B=_____.
B
A
C
2
4
2
2
1
新知巩固
例3 在Rt△ABC中,∠C=90°,∠A=15°,BC=6. 求AB的长(精确到0.01).
解:由题意知,sinA=,
则AB== .
用计算器计算,得AB≈23.18.
例题讲解
新知巩固
解:在Rt△ABC中,根据勾股定理,得
AB===10.
根据正弦、余弦的定义,得
sinA==,cosA==,
sinB==,cosB==.
1. 在Rt△ABC中,∠C=90°,AC=8,BC=6. 求sinA、cosA、sinB、cosB的值.
新知巩固
2. 在Rt△ABC中,∠C=90°,∠A=68°,AB=4. 求BC、AC的长
(精确到0.01).
解:由题意知,sinA=,cosA=,
用计算器计算,得
BC=AB×sinA=4×sin68°=4×sin68°≈3.71,
AC=AB×cosA=4×cos68°=4×cos68°≈1.50.
新知巩固
3. 在Rt△ABC中,∠C=90°,AC=BC. 求
(1) cosA;
B
A
C
解:(1)设AC=BC=k.
在Rt△ABC中,根据勾股定理,得
AB===k.
cosA===.
新知巩固
3. 在Rt△ABC中,∠C=90°,AC=BC. 求
(2) 当AB=4时,求BC的长.
B
A
C
解:(2) 由(1)得cosA==,
∵AB=4,
∴AC=4×=2,
∴BC== .
新知巩固
4. 在Rt△ABC中,∠C=90°,如果cosA=,求sinA.
解:在Rt△ABC中,cosA=,
设AC=3a,则AB=5a,
根据勾股定理,得
BC== 4a.
根据正弦的定义,得
sinA===.
利用直角三角形的三边关系求正弦、余弦值
正弦、余弦的简单应用
课堂总结
互余两角的正弦和余弦的关系
当堂检测
基础过关
1. 如图,在△ABC中,∠C=90°,BC=h,∠A=α,则AB的长为 ( )
A. h·cosα B.
C. h·sinα D.
D
B
A
C
h
α
当堂检测
基础过关
2. 在Rt△ABC中,∠C=90°,则下列式子一定成立的是( )A.sinA=sinB B.cosA=cosBC.tanA=tanB D.sinA=cosB
D
当堂检测
基础过关
3. 在Rt△ABC中,∠C=90°,若AB=13,sinA=,则BC=____.
5
4. 如图,在△ABC中,AB=AC=5,sin∠ABC=0.6. 则BC=____.
A
B
C
D
8
当堂检测
基础过关
5. 在Rt△ABC中,∠C=90°,∠A=50°,AB=5. 求BC、AC的长
(精确到0.01).
解:由题意知,sinA=,cosA=,
用计算器计算,得
BC=AB×sinA=5×sin50°=5×sin50°≈3.83,
AC=AB×cosA=5×cos50°=5×cos50°≈3.21.
当堂检测
基础过关
6. 如图:在等腰△ABC中,AB=AC=5,BC=6. 求:sinB,cosB,tanB.
A
B
C
D
由题意知,BD=BC=×6=3.
在Rt△ABD中,由勾股定理得:
AD==4.
解:过点A作AD⊥BC,垂足为D.
sinB==,
cosB==,
tanB==.
当堂检测
能力提升
7. 如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB,垂足为D. 若 AD=6,AC=8. 求sinB的值.
解: ∵ ∠ACB=∠ADC=90°,
∴∠B∠A=90°, ∠ACD∠A=90°,
∴∠B=∠ACD,
∴ sinB=sin∠ACD===.
A
B
C
D
6
8
当堂检测
能力提升
8. 如图,在正方形ABCD中,M是AD的中点,BE=3AE,求∠ECM的正切值、正弦值及余弦值.
解:设AE=x,则BE=3x,BC=4x,AM=2x,CD=4x,
∴EC==5x,EM==x,
CM==2x,
∴EM2CM2=CE2,
∴△CEM是直角三角形,∠CME=90°,
∴tan∠ECM===,
sin∠ECM===,
cos∠ECM===.
A
B
C
D
M
E
当堂检测
能力提升
1. 在△ABC中,∠C=90°,给出下列结论:
①sinA=cosB;②cosA=sinB;③sin2A+cos2A=1;④tanA=.
其中正确的有( )A.1个 B.2个 C.3个 D.4个
D
当堂检测
能力提升
2. 在Rt△ABC中,∠C=90°,tanA=2,则cosA= ( )
A. B.
C. D.
B
当堂检测
能力提升
3. 已知sin23°48′≈0.4035,若cosα=0.4035,则锐角α的度数大约为
_______.
66°12′
4. 在Rt△ABC中,∠C=90°,sinA=,则tanA·cosA的值为_____.
当堂检测
能力提升
5. 如图,在6×6正方形网格中,△ABC的顶点A,B,C都在网格线上,且都是小正方形边的中点,则sinA=____.
A
B
C
当堂检测
能力提升
6. 如图,在△ABC中,∠C=90°,点D在BC上,AD=BC=5,cos∠ADC=,求sinB的值.
A
B
C
D
解:∵AD=BC=5,cos∠ADC=,∴CD=3.
在Rt△ACD中,
∵AD=5,CD=3,
∴AC===4.
在Rt△ACB中,
∵AC=4,BC=5,
∴AB===,
∴sinB===.
D
当堂检测
能力提升
7.如图,在△ABC中,AB=AC=10,sinB=. 求sinA的值.
A
B
C
解:如图,过点C作CD⊥AB,
在Rt△CDB中,
∵sinB==,
设CD=4x,BC=5x,则BD=3x,
∴AD=10-3x,
在Rt△CDA中,由勾股定理得,AC2=AD2+CD2,
即102=(10-3x)2+(4x)2,
整理得25x2-60x=0,解得x=2.4或x=0(舍去),
∴CD=4x=9.6.
在Rt△CDA中,sinA===.
当堂检测
能力提升
8. 如图,在△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
C
A
B
D
F
解:(1)∵AC⊥BD,∴∠ACB=90°.
在Rt△ACB中,
∵cos∠ABC==,BC=8,∴AB=10,
∴AC===6,
即AC的长为6.
E
当堂检测
能力提升
8. 如图,在△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(2)求tan∠FBD的值.
C
A
B
D
F
解:(2)如图,过点F作BD的垂线,垂足为E,
∵AC⊥BD,∴AC∥EF.
∵BF为AD边上的中线,
∴CE=CD=2,EF=AC=3,
∴tan∠FBD===.
7.2 正弦、余弦(2)
第2课时 用正弦、余弦解决问题
学习目标
1. 会利用直角三角形的三边关系求直角三角形中锐角的正弦、余弦值;
2.理解直角三角形中两个锐角的正弦、余弦之间的关系;
3.能利用三角函数解决简单的直角三角形问题.
知识回顾
如何表示直角三角形中一个锐角的正弦和余弦?
锐角的正弦值、余弦值随锐角的变化是如何变化的?
知识回顾
三
角
函
数
正弦
正切
余弦
sinA==
cosA==
tanA==
A
B
C
斜边c
对边a
邻边b
例1 如图,在Rt△ABC中,∠C=90°,AC=12,BC=5. 求sinA、cosA、sinB、cosB的值.
B
A
C
解:在Rt△ABC中,根据勾股定理,得
AB===13.
根据正弦、余弦的定义,得
sinA==,cosA==,
sinB==,cosB==.
例题讲解
观察与思考
在Rt△ABC(∠C=90°)中,sinA与cosB、cosA与sinB的值有什么关系
归纳与总结
∵ sinA== ,cosA== ,
sinB== ,cosB== .
∴ sinA=cosB, cosA=sinB.
A
B
C
斜边c
对边a
邻边b
在Rt△ABC中,若∠A+∠B=90°,则sinA=cosB,cosA=sinB.
例题讲解
例2 在Rt△ABC中,∠C=90°,如果sinA=,求cosA和tanA的值.
解:在Rt△ABC中,sinA=,
设BC=2a,则AB=3a,
根据勾股定理,得
AC== .
根据余弦、正切的定义,得
cosA===,tanA==.
拓展与延伸
1. sinA与cosA有什么关系?
sin2A+cos2A=+===1.
2. tanA与sinA、cosA有什么关系?
tanA== =.
A
B
C
斜边c
对边a
邻边b
归纳与总结
同一锐角的三角函数之间的关系:
(1)sin2A+cos2A=1;
(2)tanA= .
A
B
C
斜边c
对边a
邻边b
新知巩固
(1) sinα=,则cosα=____,tanα=____,
(2) cosα=,则sinα=____,tanα=____,
(3) tanα=,则sinα=____,cosα=____.
1. 已知α为锐角:
2. 如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,则sinB=______,cosB=____,tanB=____,sin2Bcos2B=_____.
B
A
C
2
4
2
2
1
新知巩固
例3 在Rt△ABC中,∠C=90°,∠A=15°,BC=6. 求AB的长(精确到0.01).
解:由题意知,sinA=,
则AB== .
用计算器计算,得AB≈23.18.
例题讲解
新知巩固
解:在Rt△ABC中,根据勾股定理,得
AB===10.
根据正弦、余弦的定义,得
sinA==,cosA==,
sinB==,cosB==.
1. 在Rt△ABC中,∠C=90°,AC=8,BC=6. 求sinA、cosA、sinB、cosB的值.
新知巩固
2. 在Rt△ABC中,∠C=90°,∠A=68°,AB=4. 求BC、AC的长
(精确到0.01).
解:由题意知,sinA=,cosA=,
用计算器计算,得
BC=AB×sinA=4×sin68°=4×sin68°≈3.71,
AC=AB×cosA=4×cos68°=4×cos68°≈1.50.
新知巩固
3. 在Rt△ABC中,∠C=90°,AC=BC. 求
(1) cosA;
B
A
C
解:(1)设AC=BC=k.
在Rt△ABC中,根据勾股定理,得
AB===k.
cosA===.
新知巩固
3. 在Rt△ABC中,∠C=90°,AC=BC. 求
(2) 当AB=4时,求BC的长.
B
A
C
解:(2) 由(1)得cosA==,
∵AB=4,
∴AC=4×=2,
∴BC== .
新知巩固
4. 在Rt△ABC中,∠C=90°,如果cosA=,求sinA.
解:在Rt△ABC中,cosA=,
设AC=3a,则AB=5a,
根据勾股定理,得
BC== 4a.
根据正弦的定义,得
sinA===.
利用直角三角形的三边关系求正弦、余弦值
正弦、余弦的简单应用
课堂总结
互余两角的正弦和余弦的关系
当堂检测
基础过关
1. 如图,在△ABC中,∠C=90°,BC=h,∠A=α,则AB的长为 ( )
A. h·cosα B.
C. h·sinα D.
D
B
A
C
h
α
当堂检测
基础过关
2. 在Rt△ABC中,∠C=90°,则下列式子一定成立的是( )A.sinA=sinB B.cosA=cosBC.tanA=tanB D.sinA=cosB
D
当堂检测
基础过关
3. 在Rt△ABC中,∠C=90°,若AB=13,sinA=,则BC=____.
5
4. 如图,在△ABC中,AB=AC=5,sin∠ABC=0.6. 则BC=____.
A
B
C
D
8
当堂检测
基础过关
5. 在Rt△ABC中,∠C=90°,∠A=50°,AB=5. 求BC、AC的长
(精确到0.01).
解:由题意知,sinA=,cosA=,
用计算器计算,得
BC=AB×sinA=5×sin50°=5×sin50°≈3.83,
AC=AB×cosA=5×cos50°=5×cos50°≈3.21.
当堂检测
基础过关
6. 如图:在等腰△ABC中,AB=AC=5,BC=6. 求:sinB,cosB,tanB.
A
B
C
D
由题意知,BD=BC=×6=3.
在Rt△ABD中,由勾股定理得:
AD==4.
解:过点A作AD⊥BC,垂足为D.
sinB==,
cosB==,
tanB==.
当堂检测
能力提升
7. 如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB,垂足为D. 若 AD=6,AC=8. 求sinB的值.
解: ∵ ∠ACB=∠ADC=90°,
∴∠B∠A=90°, ∠ACD∠A=90°,
∴∠B=∠ACD,
∴ sinB=sin∠ACD===.
A
B
C
D
6
8
当堂检测
能力提升
8. 如图,在正方形ABCD中,M是AD的中点,BE=3AE,求∠ECM的正切值、正弦值及余弦值.
解:设AE=x,则BE=3x,BC=4x,AM=2x,CD=4x,
∴EC==5x,EM==x,
CM==2x,
∴EM2CM2=CE2,
∴△CEM是直角三角形,∠CME=90°,
∴tan∠ECM===,
sin∠ECM===,
cos∠ECM===.
A
B
C
D
M
E
当堂检测
能力提升
1. 在△ABC中,∠C=90°,给出下列结论:
①sinA=cosB;②cosA=sinB;③sin2A+cos2A=1;④tanA=.
其中正确的有( )A.1个 B.2个 C.3个 D.4个
D
当堂检测
能力提升
2. 在Rt△ABC中,∠C=90°,tanA=2,则cosA= ( )
A. B.
C. D.
B
当堂检测
能力提升
3. 已知sin23°48′≈0.4035,若cosα=0.4035,则锐角α的度数大约为
_______.
66°12′
4. 在Rt△ABC中,∠C=90°,sinA=,则tanA·cosA的值为_____.
当堂检测
能力提升
5. 如图,在6×6正方形网格中,△ABC的顶点A,B,C都在网格线上,且都是小正方形边的中点,则sinA=____.
A
B
C
当堂检测
能力提升
6. 如图,在△ABC中,∠C=90°,点D在BC上,AD=BC=5,cos∠ADC=,求sinB的值.
A
B
C
D
解:∵AD=BC=5,cos∠ADC=,∴CD=3.
在Rt△ACD中,
∵AD=5,CD=3,
∴AC===4.
在Rt△ACB中,
∵AC=4,BC=5,
∴AB===,
∴sinB===.
D
当堂检测
能力提升
7.如图,在△ABC中,AB=AC=10,sinB=. 求sinA的值.
A
B
C
解:如图,过点C作CD⊥AB,
在Rt△CDB中,
∵sinB==,
设CD=4x,BC=5x,则BD=3x,
∴AD=10-3x,
在Rt△CDA中,由勾股定理得,AC2=AD2+CD2,
即102=(10-3x)2+(4x)2,
整理得25x2-60x=0,解得x=2.4或x=0(舍去),
∴CD=4x=9.6.
在Rt△CDA中,sinA===.
当堂检测
能力提升
8. 如图,在△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
C
A
B
D
F
解:(1)∵AC⊥BD,∴∠ACB=90°.
在Rt△ACB中,
∵cos∠ABC==,BC=8,∴AB=10,
∴AC===6,
即AC的长为6.
E
当堂检测
能力提升
8. 如图,在△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(2)求tan∠FBD的值.
C
A
B
D
F
解:(2)如图,过点F作BD的垂线,垂足为E,
∵AC⊥BD,∴AC∥EF.
∵BF为AD边上的中线,
∴CE=CD=2,EF=AC=3,
∴tan∠FBD===.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
