1.1 幂的乘除 课件(共43张PPT) 2024-2025学年数学北师大版七年级下册
文档属性
| 名称 | 1.1 幂的乘除 课件(共43张PPT) 2024-2025学年数学北师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 11:00:25 | ||
图片预览











文档简介
(共43张PPT)
1.计算下列各式:
(1)102×103
(2) 105×108
(3) 10m×10n
2m×2n等于什么
() m× () n和(-3) m ×(-3) m呢 (m,n都是正整数)
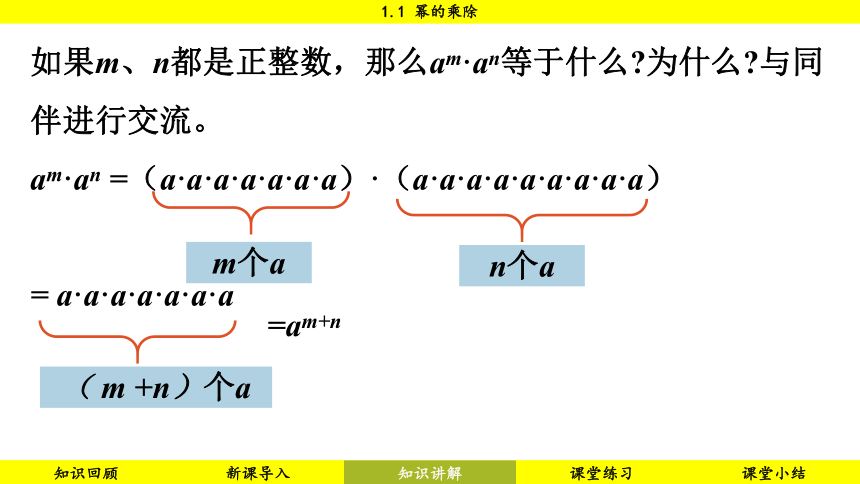
如果m、n都是正整数,那么am·an等于什么 为什么 与同伴进行交流。
am·an =(a·a·a·a·a·a·a)·(a·a·a·a·a·a·a·a·a)
= a·a·a·a·a·a·a
m个a
n个a
( m +n)个a
=am+n
即
am·an =am+n
同底数幂相乘,底数________,指数________
不变
相加
例1计算:
( -3 )7×(-3)6
=( -3 ) 7+6= ( -3 ) 13
(2) ( )3×
= ( )3+1= ( )4
(3) -x 3 x 5
= -x 3+5 = -x 8
(4) b 2m b 2m-1
= b 2m + 2m-1
= b 4m -1
例2 光在真空中传播速度约为3×108m/s,太阳光照射到地球上大约需要5×102s。地球距离太阳大约有多少米?
解:3×108×5×102=15×1010=1.5×1011(m)
因此,地球距离太阳大约有1.5×1011m
1.计算:
(1)52×57
(2)7×73×72
(3) -x2 x3
(4)(-c)3 (-c)m
2.2017年6月,我国自主研发的“神威·太湖之光”超级计算机以 1.25×1017次/s的峰值计算能力和9.3×1016次/s的持续计算能力,第三次名列世界超级计算机排名榜单TOP500第一名。该超级计算机按持续计算能力运算2×102s可做多少次运算
3.解决本课提出的比邻星与地球之间的距离问题
如图1-1,地球、木星、太阳可以近似地看成球体。木星、太阳的半径分别约为地球的10倍和102倍,它们的体积分别约为地球的多少倍
V球= —πr3 ,
其中V是球的体积,r是球的半径.
木星的半径约为地球的10倍,它的体积约为地球的10倍太阳的半径约为地球的102倍,它的体积约为地球的(102)3倍。那么,你知道(102)3等于多少吗
1.计算下列各式子,并说明理由
(1)(62)4 (2)(a2)3 (3)(am)2
2.如果m,n都是正整数,那么(am) n等于什么 为什么
(am) n= am · am · am · …… · am
n个am
= am+m+m+m+m+m……+m
= anm
n个m
即
(am) n=anm (m、n都是正整数)
幂的乘方,底数_____________ 指数___________
不变
相乘
例3 计算:
(1)(102)3
(2)(b5)5
(3)(an)3
(4)-(x2)m
(5)(y2)3
(6)2(a2)6-(a2)4
解:(1)(102)3=102×3=106;
(2)(b5)5 =b5×5=b25;
(6)2(a2)6–(a3)4=2a2×6 -a3×4
=2a12-a12
=a12.
(5)(y2)3 · y=y2×3·y=y6·y=y7;
注意:一定不要将幂的乘方与同底数幂的乘法混淆.
(3)(an)3=an×3=a3n;
(4)-(x2)m=-x2×m=-x2m;
1.计算:
(1)(103) 3
(2) -(- a3)5
(3) (x3) 5· x2
2.已知xn =2,求x2n的值。
地球可以近似地看成球体,地球的半径约为6x10km,它的体积大约多少立方千米
根据球的体积公式,地球的体积
V=r3
=( 6×103 )3 ( km 3)
1.完成下列各式,并说明理由
(1)(3×5)4=3( )×5 ( )
(2) (3×5)m=3( )×5 ( )
如果n是正整数、那么(ab) n等于什么 为什么
你能说明理由吗
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
思考下面两道题:
(1)
(2)
我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.
这两道题有什么特点?
底数为两个因式相乘,积的形式.
这种形式为积的乘方.
我们学过的幂的乘方的运算性质适用吗?
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
2.如果n是正整数,那么(ab) n等于什么 为什么
(ab)n=anbn (n为正整数)
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=anbn.
因此可得:(ab)n=anbn (n为正整数).
积的乘方法则:
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
想一想:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
(ab)n = anbn (n为正整数)
积的乘方
乘方的积
例4 计算:
(1)(3x)2
=32x2= 9x2
(2)(-2b)5
= -32b5
(3)(-2xy)4
= (-2)4x4y4=16x4y4;
(4)(3a2)n
=3n(a2)n
=3na2n.
方法总结:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏方.
1.计算
(1)(-3n)3
(2)(5xy) 3
(3)-a3+(-4a) 2a
2.解决本课提出的地球的体积问题(π取3.14)
例2 太阳可以近似地看作是球体,如果用V、R 分别代表球的体积和半径,那么V=πR3,太阳的半径约为6×105千米,它的体积大约是多少立方千米(π取3.14)
解:∵R=6×105千米,
∴V=πR3 ≈ ×3×(6×105)3
≈8.64×1017(立方千米).
答:它的体积大约是8.64×1017立方千米.
一种液体每升含有1012个有害细菌,为了试验某种杀菌剂的效果,科学家们进行了实验,发现1滴杀菌剂可以杀死109个此种细菌.要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?
1012÷109
(1)怎样列式?
(2)观察这个算式,它有何特点?
我们观察可以发现,1012 和109这两个幂的底数相同,
是同底的幂的形式.所以我们把1012 ÷109这种运算叫作同底数幂的除法.
猜想:am÷an=am-n(m>n)
验证:am÷an=
m个a
n个a
=(a·a· ··· ·a)
m-n个a
=am-n
总结归纳
(a≠0,m,n是正整数,且m>n).
am÷an=am-n
即:同底数幂相除,底数不变,指数相减.
例5 计算:
(1)a7÷a4
a7÷a4=a7-4=a3;
(2)(-x)6÷(-x)3;
(-x)6÷(-x)3=(-x)6-3
=(-x)3=-x3
(3)(xy)4÷(xy)
=(xy)4-1=(xy)3=x3y3
(4)b2m+2÷b2.
=b2m+2-2
=b2m.
(1)计算:
23÷23 23÷25 a3÷a3 a3÷a5
(2)要使的当m=n或者m<n的时候
am÷an =am-n (a≠0 m,n都是正整数) 仍然成立。
(2)个中各式的结果用幂的形式又该如何表示
(3)比较(1)(2)各式的对应结果,你有什么发现 与同伴进行交流
我们规定
即任何不等于零的数的零次幂都等于1.
即用a-p表示ap的倒数.
有了这个规定后,已学过的同底数幂的乘法和除法运算性质中的m,n就从正整数扩大到全体整数了
即am · an =am+n am÷an =am-n
(a≠0,m,n都是整数)。
例6 用小数或分数表示下列各数:
(1)10-3
(2)70×8-2
(3)1.6×10-4.
=0.001.
注意:a0 =1
=1.6×0.0001
=0.00016.
有的细胞直径只有1微米(μm ),即 0.00000m
某种计算机完成一次基本运算的时间约为1纳秒(ns),即0.000000001s;
一个氧原子的质量0.00000000000000000000000002657kg。你能用负指数表示这些数吗
用科学记数法可以很方便表示一些绝对值较大的数,同样,用科学记数法也可以表示绝对值较小的数。
一个小于1的正数可以表示为a×10n的形式
其中1≤a<10,n是负整数。
大于-1的负数也可以用类似的方法表示
如-0.00000256可以表示成-2.56×10-6
1.计算:
(1)x12÷x4
(2)(-y)3÷(-y)2
(3) -(k6÷k6)
(4)(- r) 5÷r4
(5)m÷m0
(6 )( mn ) 5÷( mn )。
2. 1个电子的质量约为0.00000000000 000 000 000 000 911kg.
(请用科学记数法表示这个数。)
同底数幂的乘法
①积的乘方
②幂的乘方
同底数幂的除法
零指数幂和负整数指数幂
科学记数法
1.计算下列各式:
(1)102×103
(2) 105×108
(3) 10m×10n
2m×2n等于什么
() m× () n和(-3) m ×(-3) m呢 (m,n都是正整数)
如果m、n都是正整数,那么am·an等于什么 为什么 与同伴进行交流。
am·an =(a·a·a·a·a·a·a)·(a·a·a·a·a·a·a·a·a)
= a·a·a·a·a·a·a
m个a
n个a
( m +n)个a
=am+n
即
am·an =am+n
同底数幂相乘,底数________,指数________
不变
相加
例1计算:
( -3 )7×(-3)6
=( -3 ) 7+6= ( -3 ) 13
(2) ( )3×
= ( )3+1= ( )4
(3) -x 3 x 5
= -x 3+5 = -x 8
(4) b 2m b 2m-1
= b 2m + 2m-1
= b 4m -1
例2 光在真空中传播速度约为3×108m/s,太阳光照射到地球上大约需要5×102s。地球距离太阳大约有多少米?
解:3×108×5×102=15×1010=1.5×1011(m)
因此,地球距离太阳大约有1.5×1011m
1.计算:
(1)52×57
(2)7×73×72
(3) -x2 x3
(4)(-c)3 (-c)m
2.2017年6月,我国自主研发的“神威·太湖之光”超级计算机以 1.25×1017次/s的峰值计算能力和9.3×1016次/s的持续计算能力,第三次名列世界超级计算机排名榜单TOP500第一名。该超级计算机按持续计算能力运算2×102s可做多少次运算
3.解决本课提出的比邻星与地球之间的距离问题
如图1-1,地球、木星、太阳可以近似地看成球体。木星、太阳的半径分别约为地球的10倍和102倍,它们的体积分别约为地球的多少倍
V球= —πr3 ,
其中V是球的体积,r是球的半径.
木星的半径约为地球的10倍,它的体积约为地球的10倍太阳的半径约为地球的102倍,它的体积约为地球的(102)3倍。那么,你知道(102)3等于多少吗
1.计算下列各式子,并说明理由
(1)(62)4 (2)(a2)3 (3)(am)2
2.如果m,n都是正整数,那么(am) n等于什么 为什么
(am) n= am · am · am · …… · am
n个am
= am+m+m+m+m+m……+m
= anm
n个m
即
(am) n=anm (m、n都是正整数)
幂的乘方,底数_____________ 指数___________
不变
相乘
例3 计算:
(1)(102)3
(2)(b5)5
(3)(an)3
(4)-(x2)m
(5)(y2)3
(6)2(a2)6-(a2)4
解:(1)(102)3=102×3=106;
(2)(b5)5 =b5×5=b25;
(6)2(a2)6–(a3)4=2a2×6 -a3×4
=2a12-a12
=a12.
(5)(y2)3 · y=y2×3·y=y6·y=y7;
注意:一定不要将幂的乘方与同底数幂的乘法混淆.
(3)(an)3=an×3=a3n;
(4)-(x2)m=-x2×m=-x2m;
1.计算:
(1)(103) 3
(2) -(- a3)5
(3) (x3) 5· x2
2.已知xn =2,求x2n的值。
地球可以近似地看成球体,地球的半径约为6x10km,它的体积大约多少立方千米
根据球的体积公式,地球的体积
V=r3
=( 6×103 )3 ( km 3)
1.完成下列各式,并说明理由
(1)(3×5)4=3( )×5 ( )
(2) (3×5)m=3( )×5 ( )
如果n是正整数、那么(ab) n等于什么 为什么
你能说明理由吗
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
(am)n=amn
am·an=am+n
思考下面两道题:
(1)
(2)
我们只能根据乘方的意义及乘法交换律、结合律可以进行运算.
这两道题有什么特点?
底数为两个因式相乘,积的形式.
这种形式为积的乘方.
我们学过的幂的乘方的运算性质适用吗?
同理:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
2.如果n是正整数,那么(ab) n等于什么 为什么
(ab)n=anbn (n为正整数)
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=anbn.
因此可得:(ab)n=anbn (n为正整数).
积的乘方法则:
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
想一想:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
(ab)n = anbn (n为正整数)
积的乘方
乘方的积
例4 计算:
(1)(3x)2
=32x2= 9x2
(2)(-2b)5
= -32b5
(3)(-2xy)4
= (-2)4x4y4=16x4y4;
(4)(3a2)n
=3n(a2)n
=3na2n.
方法总结:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏方.
1.计算
(1)(-3n)3
(2)(5xy) 3
(3)-a3+(-4a) 2a
2.解决本课提出的地球的体积问题(π取3.14)
例2 太阳可以近似地看作是球体,如果用V、R 分别代表球的体积和半径,那么V=πR3,太阳的半径约为6×105千米,它的体积大约是多少立方千米(π取3.14)
解:∵R=6×105千米,
∴V=πR3 ≈ ×3×(6×105)3
≈8.64×1017(立方千米).
答:它的体积大约是8.64×1017立方千米.
一种液体每升含有1012个有害细菌,为了试验某种杀菌剂的效果,科学家们进行了实验,发现1滴杀菌剂可以杀死109个此种细菌.要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?
1012÷109
(1)怎样列式?
(2)观察这个算式,它有何特点?
我们观察可以发现,1012 和109这两个幂的底数相同,
是同底的幂的形式.所以我们把1012 ÷109这种运算叫作同底数幂的除法.
猜想:am÷an=am-n(m>n)
验证:am÷an=
m个a
n个a
=(a·a· ··· ·a)
m-n个a
=am-n
总结归纳
(a≠0,m,n是正整数,且m>n).
am÷an=am-n
即:同底数幂相除,底数不变,指数相减.
例5 计算:
(1)a7÷a4
a7÷a4=a7-4=a3;
(2)(-x)6÷(-x)3;
(-x)6÷(-x)3=(-x)6-3
=(-x)3=-x3
(3)(xy)4÷(xy)
=(xy)4-1=(xy)3=x3y3
(4)b2m+2÷b2.
=b2m+2-2
=b2m.
(1)计算:
23÷23 23÷25 a3÷a3 a3÷a5
(2)要使的当m=n或者m<n的时候
am÷an =am-n (a≠0 m,n都是正整数) 仍然成立。
(2)个中各式的结果用幂的形式又该如何表示
(3)比较(1)(2)各式的对应结果,你有什么发现 与同伴进行交流
我们规定
即任何不等于零的数的零次幂都等于1.
即用a-p表示ap的倒数.
有了这个规定后,已学过的同底数幂的乘法和除法运算性质中的m,n就从正整数扩大到全体整数了
即am · an =am+n am÷an =am-n
(a≠0,m,n都是整数)。
例6 用小数或分数表示下列各数:
(1)10-3
(2)70×8-2
(3)1.6×10-4.
=0.001.
注意:a0 =1
=1.6×0.0001
=0.00016.
有的细胞直径只有1微米(μm ),即 0.00000m
某种计算机完成一次基本运算的时间约为1纳秒(ns),即0.000000001s;
一个氧原子的质量0.00000000000000000000000002657kg。你能用负指数表示这些数吗
用科学记数法可以很方便表示一些绝对值较大的数,同样,用科学记数法也可以表示绝对值较小的数。
一个小于1的正数可以表示为a×10n的形式
其中1≤a<10,n是负整数。
大于-1的负数也可以用类似的方法表示
如-0.00000256可以表示成-2.56×10-6
1.计算:
(1)x12÷x4
(2)(-y)3÷(-y)2
(3) -(k6÷k6)
(4)(- r) 5÷r4
(5)m÷m0
(6 )( mn ) 5÷( mn )。
2. 1个电子的质量约为0.00000000000 000 000 000 000 911kg.
(请用科学记数法表示这个数。)
同底数幂的乘法
①积的乘方
②幂的乘方
同底数幂的除法
零指数幂和负整数指数幂
科学记数法
同课章节目录
