1.3 乘法公式 课件(共38张PPT) 2024-2025学年数学北师大版七年级下册
文档属性
| 名称 | 1.3 乘法公式 课件(共38张PPT) 2024-2025学年数学北师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 11:10:35 | ||
图片预览











文档简介
(共38张PPT)
单项式乘以单项式
单项式乘以多项式
乘法分配率
乘法分配率
多项式乘以多项式
平方差公式
完全平方公式
观察以上算式及其运算结果,你有什么发现 再举两例验证你的发现。
(a+b)(a b)=a2 b2
两数和与这两数差的积,等于这两数的平方差.
公式变形:
(a–b) (a+b) =a2 b2
(b+a)( b+a )=a2 b2
平方差公式:
平方差公式
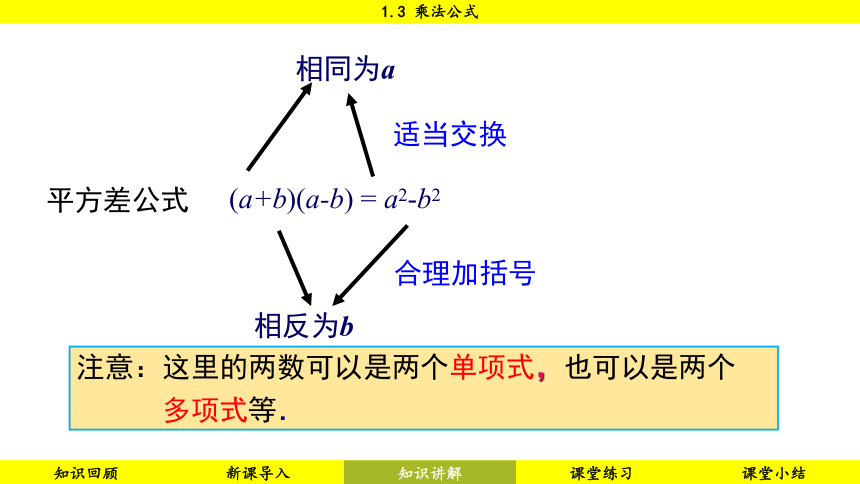
注意:这里的两数可以是两个单项式,也可以是两个
多项式等.
(a+b)(a-b) = a2-b2
相同为a
相反为b
适当交换
合理加括号
利用平方差公式计算:
(5+6x )( 5-6x ) ;
(2) (x-2y)(x+2y);
(3) (-m+n)(-m-n)
=(-m)2-n2=m2-n2.
例题1
=52-(6x)2=25-36x2;
=x2-(2y)2=x2 - 4y2;
利用平方差公式计算:
(1) (2) (ab+8)(ab-8).
=
=(ab)2-82
=a2b2-64.
例题2
如何计算(a-b)(-a-b)
你是怎样做的
计算
(1) (a+2)(a-2)
(2)(3a+2b)(3a-2b);
(3)(-x- 1)(1-x)
(4)(-4k+3)(-4k-3).
计算:
(1) 103×97; (2) 118×122.
解: 103×97
=(100+3)(100-3)
= 1002-32
=10000 – 9
=9991;
解: 118×122
=(120-2)(120+2)
= 1202-22
=14400-4
=14396.
注意:不能直接应用公式的,要经过变形才可以应用
例题3
计算:
(1)a2(a+b)(a-b)+a2b2; (2)(2x-5)(2x+5) –2x(2x-3) .
解:
(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
(2)原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
例题2
(1)计算下列各组算式
7×9= 11×13= 79×81=
8×8= 12×12= 80×80=
(2)观察上述算式及其结果,你发现什么规律?
(3)请用字母表示你发现的规律
计算
计算下列各式:
(1)(m+3) (2)(2+3x)
观察以上运算结果,你有什么发现
你能再举一些类似的例子吗?与同伴进行交流。
用自己的语言叙述这一公式!
(1)你能用图解释上面的公式吗
(2)如何计算(a-b)
你是怎样做的 与同伴进行交流。
用自己的语言叙述这一公式!
平方差公式和完全平方公式
都是重要的整式乘法公式.
例题5
例题5
计算
2.已知a+b=-3,求2a +4ab+2b 的值。
杨辉三角
我们已经知道(a+b) 展开后等于a +2ab+b ,请你利用多项式乘法法则将(a+b)3展开。
进一步,你能展开(a+b)4,(a+b)5吗
你一定发现解决上述问题需要大量的计算,是否有简单的方法呢 我们不妨找找规律!
阅读思考
如果将(a+b) n(n为非负整数)的每一项按字母a的次数由大到小排列,就可以得到下面的等式:
(a+b)=1,它只有一项,系数为1;
(a+b)=a+b,它有两项,系数分别是1,1;
(a+b)=a+2ab+b,它有三项,系数分别是1,2,1;
(a+b)=a+3ab+3ab+b,它有四项,系数分别是1,3,3,1.
阅读思考
如果将上述每个式子的各项系数排成右表,那么你能发现什么规律 观察右表,我们发现每一行的首末都是1,并且下一行的数比上一行多1个,中间各数都写在上一行两数的中间,且等于它们的和,按照这个规律可以继续将这个表写下去:
你能根据这个表得到(a+b)4,(a+b)5的结果吗
利用多项式乘法法则验证你的结果是否正确。
上表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过,而他是摘录自北宋时期数学家贾宪著的《开方作法本源》中的“开方作法本源图”(见右图),
因而人们把这个表叫做杨辉三角或贾宪三角
在欧洲这个表叫做帕斯卡三角形
帕斯卡是1654年发现这一规律的
比杨辉要迟393年,比贾宪迟600年.
怎样计算 102 ,197 更简单呢
102 197
你是怎样做的
与同伴进行交流
例题6
观察图1-12,你认为(m+n)×(m+n)点阵中的点数与m×m点阵、n×n点阵中的点数之和一样多吗?请用所学公式解释自己的结论。
观察思考
利用整式乘法公式计算
完全平方公式
(a+b)(a b)=a2 b2
公式变形:
(a–b) (a+b) =a2 b2
(b+a)( b+a )=a2 b2
平方差公式:
单项式乘以单项式
单项式乘以多项式
乘法分配率
乘法分配率
多项式乘以多项式
平方差公式
完全平方公式
观察以上算式及其运算结果,你有什么发现 再举两例验证你的发现。
(a+b)(a b)=a2 b2
两数和与这两数差的积,等于这两数的平方差.
公式变形:
(a–b) (a+b) =a2 b2
(b+a)( b+a )=a2 b2
平方差公式:
平方差公式
注意:这里的两数可以是两个单项式,也可以是两个
多项式等.
(a+b)(a-b) = a2-b2
相同为a
相反为b
适当交换
合理加括号
利用平方差公式计算:
(5+6x )( 5-6x ) ;
(2) (x-2y)(x+2y);
(3) (-m+n)(-m-n)
=(-m)2-n2=m2-n2.
例题1
=52-(6x)2=25-36x2;
=x2-(2y)2=x2 - 4y2;
利用平方差公式计算:
(1) (2) (ab+8)(ab-8).
=
=(ab)2-82
=a2b2-64.
例题2
如何计算(a-b)(-a-b)
你是怎样做的
计算
(1) (a+2)(a-2)
(2)(3a+2b)(3a-2b);
(3)(-x- 1)(1-x)
(4)(-4k+3)(-4k-3).
计算:
(1) 103×97; (2) 118×122.
解: 103×97
=(100+3)(100-3)
= 1002-32
=10000 – 9
=9991;
解: 118×122
=(120-2)(120+2)
= 1202-22
=14400-4
=14396.
注意:不能直接应用公式的,要经过变形才可以应用
例题3
计算:
(1)a2(a+b)(a-b)+a2b2; (2)(2x-5)(2x+5) –2x(2x-3) .
解:
(1)原式=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4;
(2)原式=(2x)2-25-(4x2-6x)
=4x2-25-4x2+6x
=6x-25.
例题2
(1)计算下列各组算式
7×9= 11×13= 79×81=
8×8= 12×12= 80×80=
(2)观察上述算式及其结果,你发现什么规律?
(3)请用字母表示你发现的规律
计算
计算下列各式:
(1)(m+3) (2)(2+3x)
观察以上运算结果,你有什么发现
你能再举一些类似的例子吗?与同伴进行交流。
用自己的语言叙述这一公式!
(1)你能用图解释上面的公式吗
(2)如何计算(a-b)
你是怎样做的 与同伴进行交流。
用自己的语言叙述这一公式!
平方差公式和完全平方公式
都是重要的整式乘法公式.
例题5
例题5
计算
2.已知a+b=-3,求2a +4ab+2b 的值。
杨辉三角
我们已经知道(a+b) 展开后等于a +2ab+b ,请你利用多项式乘法法则将(a+b)3展开。
进一步,你能展开(a+b)4,(a+b)5吗
你一定发现解决上述问题需要大量的计算,是否有简单的方法呢 我们不妨找找规律!
阅读思考
如果将(a+b) n(n为非负整数)的每一项按字母a的次数由大到小排列,就可以得到下面的等式:
(a+b)=1,它只有一项,系数为1;
(a+b)=a+b,它有两项,系数分别是1,1;
(a+b)=a+2ab+b,它有三项,系数分别是1,2,1;
(a+b)=a+3ab+3ab+b,它有四项,系数分别是1,3,3,1.
阅读思考
如果将上述每个式子的各项系数排成右表,那么你能发现什么规律 观察右表,我们发现每一行的首末都是1,并且下一行的数比上一行多1个,中间各数都写在上一行两数的中间,且等于它们的和,按照这个规律可以继续将这个表写下去:
你能根据这个表得到(a+b)4,(a+b)5的结果吗
利用多项式乘法法则验证你的结果是否正确。
上表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过,而他是摘录自北宋时期数学家贾宪著的《开方作法本源》中的“开方作法本源图”(见右图),
因而人们把这个表叫做杨辉三角或贾宪三角
在欧洲这个表叫做帕斯卡三角形
帕斯卡是1654年发现这一规律的
比杨辉要迟393年,比贾宪迟600年.
怎样计算 102 ,197 更简单呢
102 197
你是怎样做的
与同伴进行交流
例题6
观察图1-12,你认为(m+n)×(m+n)点阵中的点数与m×m点阵、n×n点阵中的点数之和一样多吗?请用所学公式解释自己的结论。
观察思考
利用整式乘法公式计算
完全平方公式
(a+b)(a b)=a2 b2
公式变形:
(a–b) (a+b) =a2 b2
(b+a)( b+a )=a2 b2
平方差公式:
同课章节目录
