1.1.1 同底数幂的乘法 课件(共37张PPT)2024-2025学年数学北师大版七年级下册
文档属性
| 名称 | 1.1.1 同底数幂的乘法 课件(共37张PPT)2024-2025学年数学北师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 15:50:19 | ||
图片预览










文档简介
(共37张PPT)
1.1 整式的乘法
1.1.1 同底数幂的乘法
同学们已经知道整式可以进行加减运算,
但在解决一些问题时可能需要对整式进行乘法运算.
例如,已知光在某种介质中的传播速度v及传播时间t,求光传播的距离等.
整式具体如何进行乘法运算?
比如,单项式与单项式如何相乘呢?
单项式与多项式如何相乘呢?
多项式与多项式如何相乘呢?
对于一些特殊的多项式与多项式相乘,是否可以从中总结出一些利于简便计算的公式呢?
本章将主要学习这些内容.
我国国防科技大学成功研制的“天河二号”超级计算机以每秒33.86千万亿(3.386×1016)次运算.问:它工作103s可进行多少次运算?
(1)怎样列式?
(2)观察这个算式,两个乘数1016与103有何特点?
(1)3.386×1016 ×103
(2)1016 和103这两个幂的底数相同,是同底的幂的形式.
我们把1016 ×103这种运算叫作同底数幂的乘法.
在上学期,我们已经知道
an=a·a·…·a,
n个a
其中a是有理数,n为正整数.
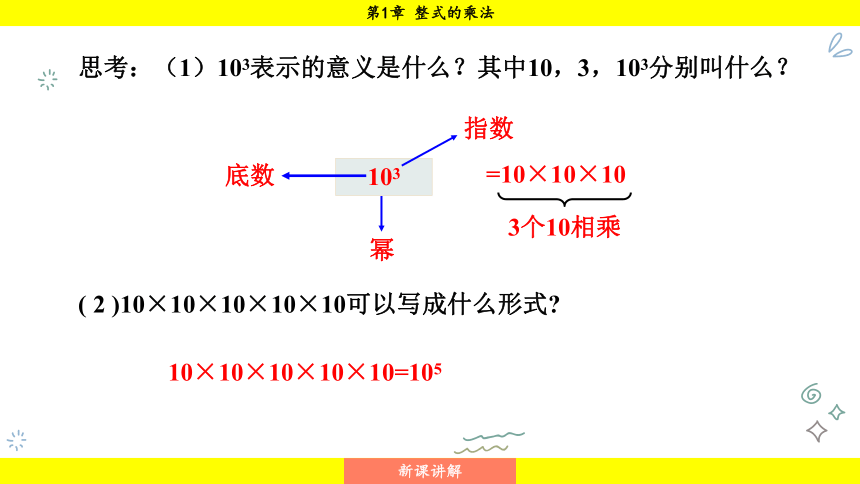
思考:(1)103表示的意义是什么?其中10,3,103分别叫什么?
( 2 )10×10×10×10×10可以写成什么形式
=10×10×10
3个10相乘
103
底数
幂
指数
10×10×10×10×10=105
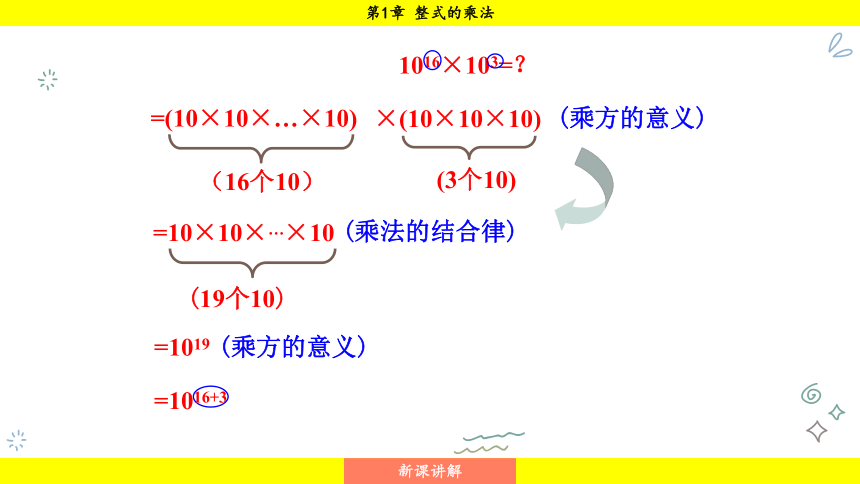
1016×103=?
=(10×10×…×10)
(16个10)
×(10×10×10)
(3个10)
=10×10×…×10
(19个10)
=1019
=1016+3
(乘方的意义)
(乘法的结合律)
(乘方的意义)
22×24= ;
a2 · a4= ;
a3 · am= (m是正整数).
由乘方的定义可知:2 ×24
=(2×2)×(2×2×2×2)
=2×2×2×2×2×2
=26.
2 个 2
4 个 2
(2+4)个 2
a ·a4
=(a·a)·(a·a·a·a)
=a·a·a·a·a·a
=a6.
(2+4)个 a
2个a
4 个a
a3·am
=(a·a·a)·(a·a·…·a)
=a·a·…·a
=a3+m.
(3+m)个 a
3个a
m个a
比较上述三个等式两端的底数和指数,你会发现什么?
底数不变,指数相加.
猜一猜
am · an =a( )
m+n
如果m,n都是正整数,那么am·an等于什么?为什么?
am·an
( 个a)
·(a·a·…·a)
( 个a)
=(a·a·…·a)
( 个a)
=a( )
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+n
m+n
=(a·a·…·a)
一般地,若m,n都是正整数,则
am·an=(a·a·…·a)·(a·a·…·a)=a·a·…·a=am+n.
m个a n个a (m+n)个 a
也就是
即同底数幂相乘,底数不变,指数相加.
am · an = am+n (m,n都是正整数).
同底数幂的乘法法则
结果:①底数不变
②指数相加
注意:
条件:①乘法
②底数相同
例1 计算:
(1)105×103; (2)x3·x4.
解(1)105×103=105+3=108.
(2)x3·x4=x3+4=x7.
下列计算对不对?如果不对,应怎样改正?
(1)a2.a5=a10;
(2)a3.a3=2a6;
(3)a·a4=a4.
例2 计算:
(1)-a·a3 ; (2)-yn·yn+1(n是正整数).
解(1)-a·a3=(-1)·a1+3=-a4.
(2)-yn·yn+1=(-1)·yn+n+1= -y2n+1.
解:(1)原式=(-3)7+6=(-3)13;
(2)原式=
(3)原式=
(4)原式=
计算:
(1) (-3)7×(-3)6;
(2)
(3)-x3·x5;
(4)b2m·b2m+1 .
-x3+5= -x8;
b2m+2m+1=b4m+1.
提醒:
计算同底数幂的乘法时,
要注意算式里面的负号是属于幂的
还是属于底数的.
判断(正确的打“√”,错误的打“×”)
(1)x4·x6=x24 ( ) (2) x·x3=x3 ( )
(3) x4+x4=x8 ( ) (4) x2·x2=2x4 ( )
(5)(-x)2 · (-x)3 = (-x)5 ( )
(6)a2·a3- a3·a2 = 0 ( )
(7)x3·y5=(xy)8 ( )
(8) x7+x7=x14 ( )
√
√
×
×
×
×
×
×
对于计算出错的题目,你能分析出错的原因吗?试试看!
a · a6 · a3
类比同底数幂的乘法公式am · an = am+n (当m、n都是正整数)
am· an· ap = am+n+p (m、n、p都是正整数)
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示 等于什么呢?
am · an · ap
比一比
= a7 · a3 =a10
想一想
例3 计算:
(1)y·y2·y4; (2)(-x)×(-x2)×(-x3).
解(1)y·y ·y4=(y·y )·y4=y3·y4=y7.
(2)(-x)×(-x2)×(-x3)= -(x·x2·x3)
= -(x3·x3)
= -x6.
例3还可以这样计算:
(1)y·y2·y4=y1+2+4 = y7 .
(2)(-x)×(-x2)×(-x3)= -x1+2+3 = -x6 .
am·an·ak=?(m,n,k都是正整数)
光在真空中的速度约为3×108m/s,太阳光照射到地球上大约需要5×102m/s.地球距离太阳大约有多远?
解:3×108×5×102
=15×1010
=1.5×1011(m).
答:地球距离太阳大约有1.5×1011m.
1 计算:
(1)56×54; (2)x·x3;
(3)(-2)3×(-2)4; (4)-a5·a5;
(5)xm+1·xm-1(其中m>1,且m是正整数).
2 计算:
(1)x2·x3·x4;
(2)(-x)×x3×(-x5);
(3)xn·xn+1·xn+2(n是正整数).
1.下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
(2)b3+b3=b6
(3)a·a5·a3=a8
(4)(-x)4·(-x)4=(-x)16
×
×
×
×
b3·b3=b6
b3+b3=2b3
=x8
a·a5·a3=a9
(-x)4·(-x)4=(-x)8
(1)x·x2·x( )=x7;
(2)xm·( )=x3m;
(3)8×4=2x,则x=( ).
23×22=25
4
5
x2m
2.填空:
A组
(1)(-9)2×93
(2)(a-b)2·(a-b)3
(3)-a4·(-a)2
3.计算下列各题:
注意符号哟!
B组
(1) xn+1·x2n
(2)
(3)
a·a2+a3
=92×93=95
=(a-b)5
=-a4·a2
=-a6
=x3n+1
=a3+a3=2a6
公式中的底数和指数可以是一个数、字母或一个式子.
注意:
(1)已知an-3·a2n+1=a10,求n的值;
公式运用:am·an=am+n
解:n-3+2n+1=10,
n=4;
4.创新应用.
(2)已知xa=2,xb=3,求xa+b的值.
公式逆用:am+n=am·an
解:xa+b=xa·xb=2×3=6.
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数,再应用法则
1.1 整式的乘法
1.1.1 同底数幂的乘法
同学们已经知道整式可以进行加减运算,
但在解决一些问题时可能需要对整式进行乘法运算.
例如,已知光在某种介质中的传播速度v及传播时间t,求光传播的距离等.
整式具体如何进行乘法运算?
比如,单项式与单项式如何相乘呢?
单项式与多项式如何相乘呢?
多项式与多项式如何相乘呢?
对于一些特殊的多项式与多项式相乘,是否可以从中总结出一些利于简便计算的公式呢?
本章将主要学习这些内容.
我国国防科技大学成功研制的“天河二号”超级计算机以每秒33.86千万亿(3.386×1016)次运算.问:它工作103s可进行多少次运算?
(1)怎样列式?
(2)观察这个算式,两个乘数1016与103有何特点?
(1)3.386×1016 ×103
(2)1016 和103这两个幂的底数相同,是同底的幂的形式.
我们把1016 ×103这种运算叫作同底数幂的乘法.
在上学期,我们已经知道
an=a·a·…·a,
n个a
其中a是有理数,n为正整数.
思考:(1)103表示的意义是什么?其中10,3,103分别叫什么?
( 2 )10×10×10×10×10可以写成什么形式
=10×10×10
3个10相乘
103
底数
幂
指数
10×10×10×10×10=105
1016×103=?
=(10×10×…×10)
(16个10)
×(10×10×10)
(3个10)
=10×10×…×10
(19个10)
=1019
=1016+3
(乘方的意义)
(乘法的结合律)
(乘方的意义)
22×24= ;
a2 · a4= ;
a3 · am= (m是正整数).
由乘方的定义可知:2 ×24
=(2×2)×(2×2×2×2)
=2×2×2×2×2×2
=26.
2 个 2
4 个 2
(2+4)个 2
a ·a4
=(a·a)·(a·a·a·a)
=a·a·a·a·a·a
=a6.
(2+4)个 a
2个a
4 个a
a3·am
=(a·a·a)·(a·a·…·a)
=a·a·…·a
=a3+m.
(3+m)个 a
3个a
m个a
比较上述三个等式两端的底数和指数,你会发现什么?
底数不变,指数相加.
猜一猜
am · an =a( )
m+n
如果m,n都是正整数,那么am·an等于什么?为什么?
am·an
( 个a)
·(a·a·…·a)
( 个a)
=(a·a·…·a)
( 个a)
=a( )
(乘方的意义)
(乘法的结合律)
(乘方的意义)
m
n
m+n
m+n
=(a·a·…·a)
一般地,若m,n都是正整数,则
am·an=(a·a·…·a)·(a·a·…·a)=a·a·…·a=am+n.
m个a n个a (m+n)个 a
也就是
即同底数幂相乘,底数不变,指数相加.
am · an = am+n (m,n都是正整数).
同底数幂的乘法法则
结果:①底数不变
②指数相加
注意:
条件:①乘法
②底数相同
例1 计算:
(1)105×103; (2)x3·x4.
解(1)105×103=105+3=108.
(2)x3·x4=x3+4=x7.
下列计算对不对?如果不对,应怎样改正?
(1)a2.a5=a10;
(2)a3.a3=2a6;
(3)a·a4=a4.
例2 计算:
(1)-a·a3 ; (2)-yn·yn+1(n是正整数).
解(1)-a·a3=(-1)·a1+3=-a4.
(2)-yn·yn+1=(-1)·yn+n+1= -y2n+1.
解:(1)原式=(-3)7+6=(-3)13;
(2)原式=
(3)原式=
(4)原式=
计算:
(1) (-3)7×(-3)6;
(2)
(3)-x3·x5;
(4)b2m·b2m+1 .
-x3+5= -x8;
b2m+2m+1=b4m+1.
提醒:
计算同底数幂的乘法时,
要注意算式里面的负号是属于幂的
还是属于底数的.
判断(正确的打“√”,错误的打“×”)
(1)x4·x6=x24 ( ) (2) x·x3=x3 ( )
(3) x4+x4=x8 ( ) (4) x2·x2=2x4 ( )
(5)(-x)2 · (-x)3 = (-x)5 ( )
(6)a2·a3- a3·a2 = 0 ( )
(7)x3·y5=(xy)8 ( )
(8) x7+x7=x14 ( )
√
√
×
×
×
×
×
×
对于计算出错的题目,你能分析出错的原因吗?试试看!
a · a6 · a3
类比同底数幂的乘法公式am · an = am+n (当m、n都是正整数)
am· an· ap = am+n+p (m、n、p都是正整数)
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示 等于什么呢?
am · an · ap
比一比
= a7 · a3 =a10
想一想
例3 计算:
(1)y·y2·y4; (2)(-x)×(-x2)×(-x3).
解(1)y·y ·y4=(y·y )·y4=y3·y4=y7.
(2)(-x)×(-x2)×(-x3)= -(x·x2·x3)
= -(x3·x3)
= -x6.
例3还可以这样计算:
(1)y·y2·y4=y1+2+4 = y7 .
(2)(-x)×(-x2)×(-x3)= -x1+2+3 = -x6 .
am·an·ak=?(m,n,k都是正整数)
光在真空中的速度约为3×108m/s,太阳光照射到地球上大约需要5×102m/s.地球距离太阳大约有多远?
解:3×108×5×102
=15×1010
=1.5×1011(m).
答:地球距离太阳大约有1.5×1011m.
1 计算:
(1)56×54; (2)x·x3;
(3)(-2)3×(-2)4; (4)-a5·a5;
(5)xm+1·xm-1(其中m>1,且m是正整数).
2 计算:
(1)x2·x3·x4;
(2)(-x)×x3×(-x5);
(3)xn·xn+1·xn+2(n是正整数).
1.下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
(2)b3+b3=b6
(3)a·a5·a3=a8
(4)(-x)4·(-x)4=(-x)16
×
×
×
×
b3·b3=b6
b3+b3=2b3
=x8
a·a5·a3=a9
(-x)4·(-x)4=(-x)8
(1)x·x2·x( )=x7;
(2)xm·( )=x3m;
(3)8×4=2x,则x=( ).
23×22=25
4
5
x2m
2.填空:
A组
(1)(-9)2×93
(2)(a-b)2·(a-b)3
(3)-a4·(-a)2
3.计算下列各题:
注意符号哟!
B组
(1) xn+1·x2n
(2)
(3)
a·a2+a3
=92×93=95
=(a-b)5
=-a4·a2
=-a6
=x3n+1
=a3+a3=2a6
公式中的底数和指数可以是一个数、字母或一个式子.
注意:
(1)已知an-3·a2n+1=a10,求n的值;
公式运用:am·an=am+n
解:n-3+2n+1=10,
n=4;
4.创新应用.
(2)已知xa=2,xb=3,求xa+b的值.
公式逆用:am+n=am·an
解:xa+b=xa·xb=2×3=6.
同底数幂的乘法
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
am·an·ap=am+n+p(m,n,p都是正整数)
直接应用法则
常见变形:(-a)2=a2, (-a)3=-a3
底数相同时
底数不相同时
先变成同底数,再应用法则
同课章节目录
