1.2.2 第1课时 完全平方公式 课件(共26张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 1.2.2 第1课时 完全平方公式 课件(共26张PPT)2024-2025学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
1.2 乘法公式
1.2.2 完全平方公式
第1课时 完全平方公式
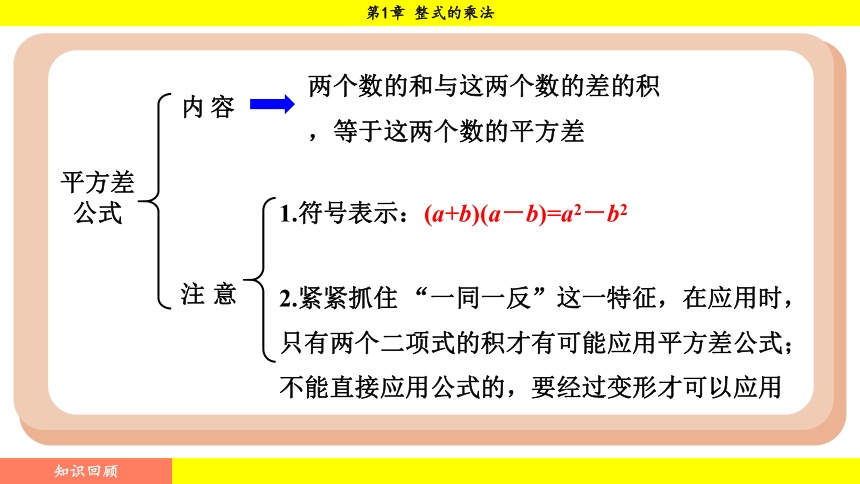
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
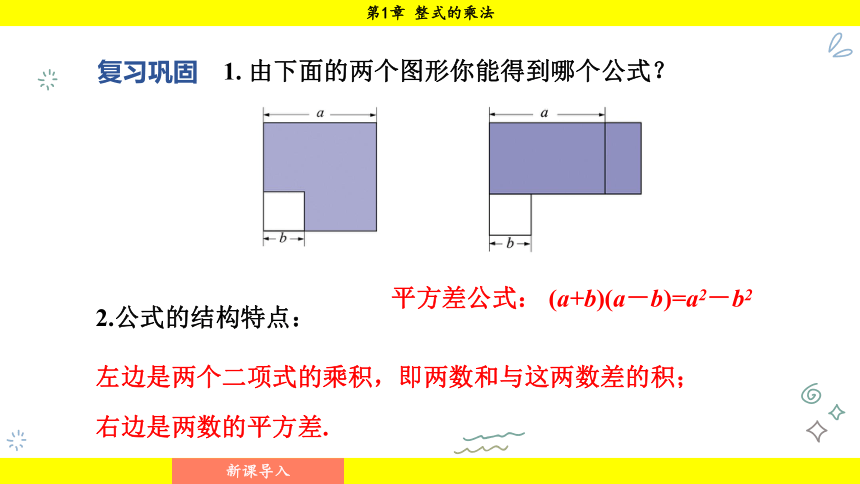
2.公式的结构特点:
左边是两个二项式的乘积,即两数和与这两数差的积;右边是两数的平方差.
1. 由下面的两个图形你能得到哪个公式?
复习巩固
平方差公式: (a+b)(a-b)=a2-b2
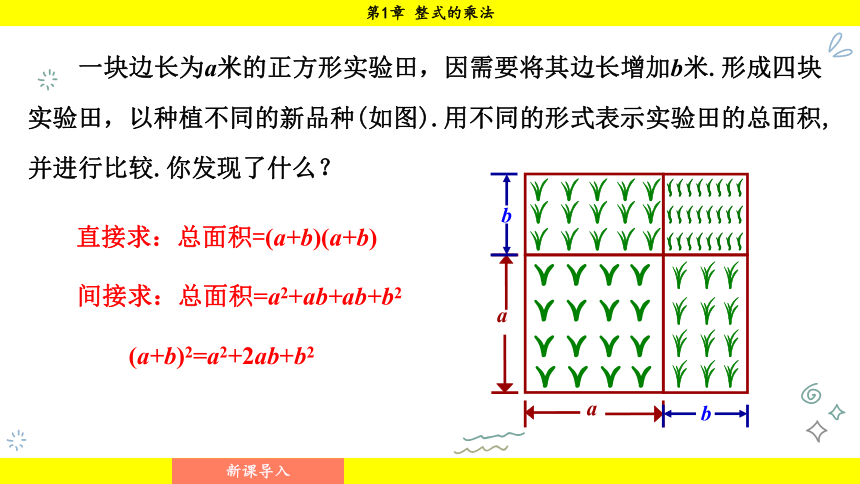
一块边长为a米的正方形实验田,因需要将其边长增加b米.形成四块实验田,以种植不同的新品种(如图).用不同的形式表示实验田的总面积, 并进行比较.你发现了什么?
a
a
b
b
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
(a+b)2=a2+2ab+b2
计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p-1)2=(p-1)(p-1)= .
p2-2p+1
(4) (m-2)2=(m-2)(m-2)= .
m2-4m+4
计算:(x+y) .
由多项式与多项式相乘的法则可得
(x+y) =(x+y)(x+y)
= x + xy + yx + y
= x + 2xy + y .
于是得到了完全平方公式 1:
(x+y) = x + 2xy + y2 .
即多项式 x + y 的平方等于 x 与 y 的平方和加上 x 与 y 的积的 2 倍.
若将完全平方公式 1 中的 y 用 –y 代替,则可得
(x-y) = x + 2x·(-y)+(-y) = x - 2xy + y .
于是得到了完全平方公式 2:
(x-y)2 = x - 2xy + y .
即多项式 x-y 的平方等于 x 与 y 的平方和减去 x 与 y 的积的 2 倍.
设 a,b 都是正数,
将完全平方公式 1 中的 x 用 a 代入,y 用 b 代入,可得
(a+b) = a + 2ab + b .
如图,把一个边长为 a+b 的正方形分割成四部分,
这四部分的面积分别为 ab,b ,a ,ba,
于是(a+b) = ab + b + a + ba = a + 2ab + b .
实质上,这就是完全平方公式 1 的几何背景.
几何解释:
(a+b)2= .
a2+2ab+b2
和的完全平方公式:
a
a
b
b
=
+
+
+
a2
ab
ab
b2
a2
ab b(a b)
=a2 2ab+b2 .
=
(a b)2
a b
a b
a
a
ab
b(a b)
b
b
(a b)2
几何解释:
(a-b)2= .
a2-2ab+b2
差的完全平方公式:
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的 2 倍.
这两个公式叫作完全平方公式.
简记为:
“首平方,尾平方,积的2倍放中间”
公式特征:
1.积为二次三项式;
2.积中的两项为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同.
4.公式中的字母a,b可以表示数,单项式和多项式.
例5 运用完全平方公式计算:
(1)(a+)2;
(2)(3m+n)2;
(3)(2x-3y)2.
解(1)将完全平方公式 1 中的 x 用 a 代入,y 用 代入,可得
(a + )2 = a + 2·a· +()2
= a + a + .
(2)将完全平方公式 1 中的 x 用 3m 代入,y 用 n 代入,可得
(3m+n)2 =(3m)2 + 2·3m·n + n2
= 9m + 6mn + n .
(3)将完全平方公式 2 中的 x 用 2x 代替,y 用 3y 代替,可得
(2x-3y) =(2x) - 2·2x·3y +(3y)
= 4x - 12xy + 9y .
填表:
有了完全平方公式,x,y分别用任何数代入,或者用任意多项式代入,从完全平方公式可以得到许多有关数或多项式的等式.
算式 与公式中x对应的项 与公式中y对应的项 计算结果
(2a+b)2
(5a-4b)2
2a
b
5a
4b
4a2+b2+4ab
25a2+16b2-40ab
运用完全平方公式计算:
解: (2x-3)2=
=4x2
(1)(2x-3)2;
( a- b )2 = a2 - 2ab + b2
(2x)2
-2 (2x) 3
+32
-12x
+9;
(a + b)2= a2 + 2ab + b2
y2
(2) ( y+ )2.
=y2
+ y
+
+ ( )2
+ 2 y
解:( y+ )2 =
运用完全平方公式计算:
解:∵36x2+(m+1)xy+25y2
=(±6x)2+(m+1)xy+(±5y)2,
∴(m+1)xy=±2·6x·5y,
∴m+1=±60,
∴m=59或-61.
方法总结:两数的平方和加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.
如果36x2+(m+1)xy+25y2是一个完全平方式,求m的值.
能否用去括号法则检查添括号是否正确
1.在等号右边的括号内填上适当的项:
(1)a+b-c=a+( )
(2)a-b+c=a-( )
(3)a-b-c=a-( )
(4)a+b+c=a-( )
b-c
b-c
b+c
-b-c
2.下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (-x +y)2 =x2+2xy +y2
(4) (2x+y)2 =4x2 +2xy +y2
×
×
×
×
x2+2xy +y2
x2-2xy +y2
x2 -2xy +y2
4x2+4xy +y2
(1) (6a+5b)2;
=36a2+60ab+25b2;
(2) (4x-3y)2 ;
=16x2-24xy+9y2;
(3) (2m-1)2 ;
=4m2-4m+1;
(4)(-2m-1)2 .
=4m2+4m+1.
3.运用完全平方公式计算:
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,需要先添括号变形
3.弄清完全平方公式和平方差公式的不同点(从公式结构特点及结果两方面)
1.2 乘法公式
1.2.2 完全平方公式
第1课时 完全平方公式
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用
2.公式的结构特点:
左边是两个二项式的乘积,即两数和与这两数差的积;右边是两数的平方差.
1. 由下面的两个图形你能得到哪个公式?
复习巩固
平方差公式: (a+b)(a-b)=a2-b2
一块边长为a米的正方形实验田,因需要将其边长增加b米.形成四块实验田,以种植不同的新品种(如图).用不同的形式表示实验田的总面积, 并进行比较.你发现了什么?
a
a
b
b
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
(a+b)2=a2+2ab+b2
计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p-1)2=(p-1)(p-1)= .
p2-2p+1
(4) (m-2)2=(m-2)(m-2)= .
m2-4m+4
计算:(x+y) .
由多项式与多项式相乘的法则可得
(x+y) =(x+y)(x+y)
= x + xy + yx + y
= x + 2xy + y .
于是得到了完全平方公式 1:
(x+y) = x + 2xy + y2 .
即多项式 x + y 的平方等于 x 与 y 的平方和加上 x 与 y 的积的 2 倍.
若将完全平方公式 1 中的 y 用 –y 代替,则可得
(x-y) = x + 2x·(-y)+(-y) = x - 2xy + y .
于是得到了完全平方公式 2:
(x-y)2 = x - 2xy + y .
即多项式 x-y 的平方等于 x 与 y 的平方和减去 x 与 y 的积的 2 倍.
设 a,b 都是正数,
将完全平方公式 1 中的 x 用 a 代入,y 用 b 代入,可得
(a+b) = a + 2ab + b .
如图,把一个边长为 a+b 的正方形分割成四部分,
这四部分的面积分别为 ab,b ,a ,ba,
于是(a+b) = ab + b + a + ba = a + 2ab + b .
实质上,这就是完全平方公式 1 的几何背景.
几何解释:
(a+b)2= .
a2+2ab+b2
和的完全平方公式:
a
a
b
b
=
+
+
+
a2
ab
ab
b2
a2
ab b(a b)
=a2 2ab+b2 .
=
(a b)2
a b
a b
a
a
ab
b(a b)
b
b
(a b)2
几何解释:
(a-b)2= .
a2-2ab+b2
差的完全平方公式:
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的 2 倍.
这两个公式叫作完全平方公式.
简记为:
“首平方,尾平方,积的2倍放中间”
公式特征:
1.积为二次三项式;
2.积中的两项为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同.
4.公式中的字母a,b可以表示数,单项式和多项式.
例5 运用完全平方公式计算:
(1)(a+)2;
(2)(3m+n)2;
(3)(2x-3y)2.
解(1)将完全平方公式 1 中的 x 用 a 代入,y 用 代入,可得
(a + )2 = a + 2·a· +()2
= a + a + .
(2)将完全平方公式 1 中的 x 用 3m 代入,y 用 n 代入,可得
(3m+n)2 =(3m)2 + 2·3m·n + n2
= 9m + 6mn + n .
(3)将完全平方公式 2 中的 x 用 2x 代替,y 用 3y 代替,可得
(2x-3y) =(2x) - 2·2x·3y +(3y)
= 4x - 12xy + 9y .
填表:
有了完全平方公式,x,y分别用任何数代入,或者用任意多项式代入,从完全平方公式可以得到许多有关数或多项式的等式.
算式 与公式中x对应的项 与公式中y对应的项 计算结果
(2a+b)2
(5a-4b)2
2a
b
5a
4b
4a2+b2+4ab
25a2+16b2-40ab
运用完全平方公式计算:
解: (2x-3)2=
=4x2
(1)(2x-3)2;
( a- b )2 = a2 - 2ab + b2
(2x)2
-2 (2x) 3
+32
-12x
+9;
(a + b)2= a2 + 2ab + b2
y2
(2) ( y+ )2.
=y2
+ y
+
+ ( )2
+ 2 y
解:( y+ )2 =
运用完全平方公式计算:
解:∵36x2+(m+1)xy+25y2
=(±6x)2+(m+1)xy+(±5y)2,
∴(m+1)xy=±2·6x·5y,
∴m+1=±60,
∴m=59或-61.
方法总结:两数的平方和加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.
如果36x2+(m+1)xy+25y2是一个完全平方式,求m的值.
能否用去括号法则检查添括号是否正确
1.在等号右边的括号内填上适当的项:
(1)a+b-c=a+( )
(2)a-b+c=a-( )
(3)a-b-c=a-( )
(4)a+b+c=a-( )
b-c
b-c
b+c
-b-c
2.下面各式的计算是否正确?如果不正确,应当怎样改正?
(1)(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (-x +y)2 =x2+2xy +y2
(4) (2x+y)2 =4x2 +2xy +y2
×
×
×
×
x2+2xy +y2
x2-2xy +y2
x2 -2xy +y2
4x2+4xy +y2
(1) (6a+5b)2;
=36a2+60ab+25b2;
(2) (4x-3y)2 ;
=16x2-24xy+9y2;
(3) (2m-1)2 ;
=4m2-4m+1;
(4)(-2m-1)2 .
=4m2+4m+1.
3.运用完全平方公式计算:
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,需要先添括号变形
3.弄清完全平方公式和平方差公式的不同点(从公式结构特点及结果两方面)
同课章节目录
