2.3.1 认识实数 课件(共40张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 2.3.1 认识实数 课件(共40张PPT)2024-2025学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 00:00:00 | ||
图片预览









文档简介
(共40张PPT)
2.3 实数
2.3.1 认识实数
在七年级上册已经认识了有理数,它是如何分类的?
下列各数中,哪些是无理数?
0.,,-,,-,
0.101001…(相邻两个1之间逐次增加一个0).
由无理数的定义可知,
,-,0.101001…(相邻两个1之间逐次增加一个0)是无理数.
到目前为止,我们认识了有理数和无理数,
并将有理数和无理数统称为实数.
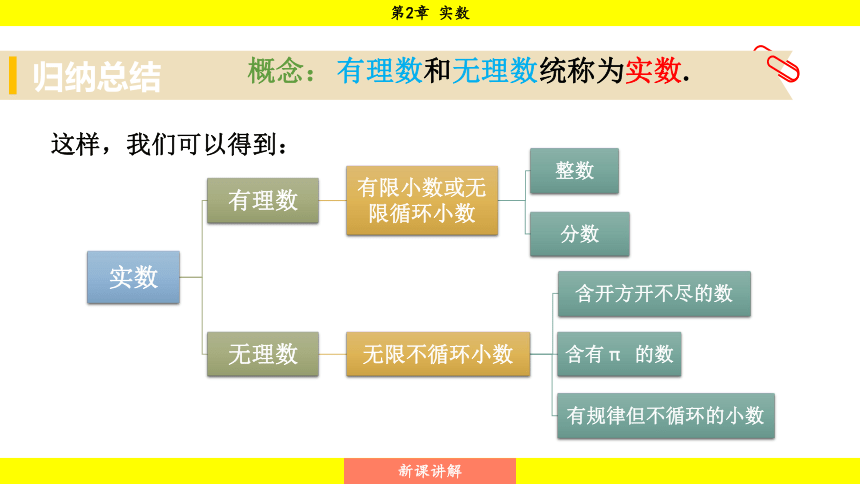
于是实数可以分类如下:
有理数和无理数统称为实数.
这样,我们可以得到:
概念:
每一个有理数都可以用数轴上唯一的点来表示,那么每一个无理数(如)是否也可以用数轴上唯一的点来表示呢?
前面已经构造出了一个边长为的正方形.
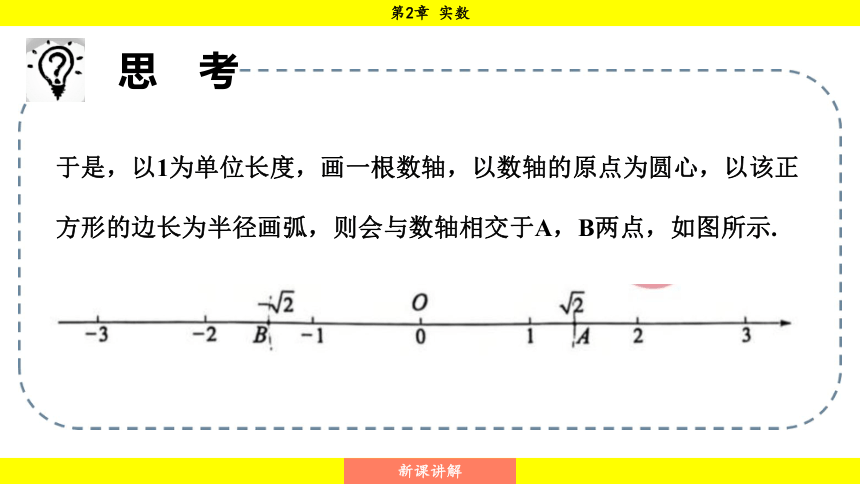
于是,以1为单位长度,画一根数轴,以数轴的原点为圆心,以该正方形的边长为半径画弧,则会与数轴相交于A,B两点,如图所示.
于是,数轴上有唯一的点A和点B分别表示和.
事实上,每一个无理数都可以用数轴上唯一的点来表示.
综上可知:每一个实数都可以用数轴上唯一的点来表示.
反过来,还可以说明:数轴上每一个点都表示唯一的实数.
将上面两个结论合起来,可以简洁地说成:
实数和数轴上的点一一对应.
如何用数轴上的点表示无理数-
我们已经知道,一个面积为8的正方形的边长是 .因此我们以数轴的原点O为圆心,以正方形的边长为半径画弧,与正半轴的交点M就表示,与负半轴的交点N就表示 - ,这样,我们就分别用数轴上唯一的一个点表示出来无理数- .
0
1
2
3
-1
-2
-3
O
M
N
-
实数分为正实数、零、负实数.
与规定有理数的大小一样,
规定正实数都大于0,
负实数都小于0.
数轴上表示正实数的点在原点右边,
表示负实数的点在原点左边.
我们可以得到:
0
正实数
负实数
如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
解析:∵ ≈1.414,
∴ 和5.1之间的整数有2,3,4,5,
∴A,B两点之间表示整数的点共有4个.
C
【方法总结】
数轴上的点与实数一一对应,
结合数轴分析,
可轻松得出结论.
与有理数一样,如果两个实数只有符号不同,
那么其中的一个数叫作另一个数的相反数,
也称它们互为相反数.
例如,和互为相反数,0的相反数是0.
我们把实数a的相反数记作 -a.
实数的绝对值意义也与有理数一样:
正实数的绝对值是它本身,
负实数的绝对值是它的相反数,
0的绝对值是0.
例如, =, = .
设a表示一个实数,则
1. a 是一个实数,实数 a 的相反数为 –a .
2.①一个正实数的绝对值是它本身;
②一个负实数的绝对值是它的相反数;
③ 0 的绝对值是 0.
1.分别求下列各数的相反数、倒数和绝对值.
解:(1)∵ =-4,
∴ 的相反数是4,倒数是 - ,绝对值是4.
1.分别求下列各数的相反数、倒数和绝对值.
(2)∵ =15,
∴ 的相反数是-15,倒数是 ,绝对值是15.
(3) 的相反数是- ,倒数是 ,绝对值是 .
2. (1)的相反数是 ,
π 的相反数是 ,
的相反数是 .
(2)-π 的绝对值是 ,
∣∣= ,
∣0∣ = .
0
π
例1 求下列各数的相反数和绝对值:
(1); (2).
解 (1)的相反数是, = .
(2)的相反数是, = .
解: 因为
所以, 的相反数为
由绝对值的意义得:
求 的相反数和绝对值:
如图所示,数轴上A,B两点表示的数分别为-1和 ,点B关于点A的对称点为C,求点C所表示的实数.
解:∵数轴上A,B两点表示的数分别为-1和 ,
∴点B到点A的距离为1+ ,则点 C 到点 A 的距离为1+ ,
设点C表示的实数为x,则点A到点C的距离为-1-x,
∴-1-x=1+ ,
∴ x=-2-
方法总结
本题主要考查了实数与数轴之间的对应关系,其中利用了:当点 C 为点 B 关于点 A 的对称点时,点 C 到点 A的距离等于点 B 到点 A 的距离;
两点之间的距离为两数差的绝对值.
1 把下列各数填入相应的框内:
,,, ,,,1.3,0,18,,.
2 判断(正确的画“√”,错误的画“×”):
(1)任何一个无理数的绝对值都是正数;( )
(2)不带根号的数都是有理数;( )
(3)实数可以分为正实数和负实数两类.( )
√
×
×
3 求下列各数的相反数和绝对值:
(1);
(2) ;
(3).
(3) 的相反数是_______,绝对值是________;
1.填空.
(1)3.14的相反数是_______,绝对值是________;
(2) 的相反数是_______,绝对值是________;
-3.14
3.14
(5)点A在数轴上表示的数为 ,点B在数轴上对应的数为 ,则A,B两点的距离为_________.
(4) 的相反数是__________,绝对值是___________;
2.如图,在数轴上点A和点B之间的整数是 .
【解析】1< <2,2< <3,在 与 之间的整数是2.
A
B
2
2.3 实数
2.3.1 认识实数
在七年级上册已经认识了有理数,它是如何分类的?
下列各数中,哪些是无理数?
0.,,-,,-,
0.101001…(相邻两个1之间逐次增加一个0).
由无理数的定义可知,
,-,0.101001…(相邻两个1之间逐次增加一个0)是无理数.
到目前为止,我们认识了有理数和无理数,
并将有理数和无理数统称为实数.
于是实数可以分类如下:
有理数和无理数统称为实数.
这样,我们可以得到:
概念:
每一个有理数都可以用数轴上唯一的点来表示,那么每一个无理数(如)是否也可以用数轴上唯一的点来表示呢?
前面已经构造出了一个边长为的正方形.
于是,以1为单位长度,画一根数轴,以数轴的原点为圆心,以该正方形的边长为半径画弧,则会与数轴相交于A,B两点,如图所示.
于是,数轴上有唯一的点A和点B分别表示和.
事实上,每一个无理数都可以用数轴上唯一的点来表示.
综上可知:每一个实数都可以用数轴上唯一的点来表示.
反过来,还可以说明:数轴上每一个点都表示唯一的实数.
将上面两个结论合起来,可以简洁地说成:
实数和数轴上的点一一对应.
如何用数轴上的点表示无理数-
我们已经知道,一个面积为8的正方形的边长是 .因此我们以数轴的原点O为圆心,以正方形的边长为半径画弧,与正半轴的交点M就表示,与负半轴的交点N就表示 - ,这样,我们就分别用数轴上唯一的一个点表示出来无理数- .
0
1
2
3
-1
-2
-3
O
M
N
-
实数分为正实数、零、负实数.
与规定有理数的大小一样,
规定正实数都大于0,
负实数都小于0.
数轴上表示正实数的点在原点右边,
表示负实数的点在原点左边.
我们可以得到:
0
正实数
负实数
如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有( )
A.6个 B.5个 C.4个 D.3个
解析:∵ ≈1.414,
∴ 和5.1之间的整数有2,3,4,5,
∴A,B两点之间表示整数的点共有4个.
C
【方法总结】
数轴上的点与实数一一对应,
结合数轴分析,
可轻松得出结论.
与有理数一样,如果两个实数只有符号不同,
那么其中的一个数叫作另一个数的相反数,
也称它们互为相反数.
例如,和互为相反数,0的相反数是0.
我们把实数a的相反数记作 -a.
实数的绝对值意义也与有理数一样:
正实数的绝对值是它本身,
负实数的绝对值是它的相反数,
0的绝对值是0.
例如, =, = .
设a表示一个实数,则
1. a 是一个实数,实数 a 的相反数为 –a .
2.①一个正实数的绝对值是它本身;
②一个负实数的绝对值是它的相反数;
③ 0 的绝对值是 0.
1.分别求下列各数的相反数、倒数和绝对值.
解:(1)∵ =-4,
∴ 的相反数是4,倒数是 - ,绝对值是4.
1.分别求下列各数的相反数、倒数和绝对值.
(2)∵ =15,
∴ 的相反数是-15,倒数是 ,绝对值是15.
(3) 的相反数是- ,倒数是 ,绝对值是 .
2. (1)的相反数是 ,
π 的相反数是 ,
的相反数是 .
(2)-π 的绝对值是 ,
∣∣= ,
∣0∣ = .
0
π
例1 求下列各数的相反数和绝对值:
(1); (2).
解 (1)的相反数是, = .
(2)的相反数是, = .
解: 因为
所以, 的相反数为
由绝对值的意义得:
求 的相反数和绝对值:
如图所示,数轴上A,B两点表示的数分别为-1和 ,点B关于点A的对称点为C,求点C所表示的实数.
解:∵数轴上A,B两点表示的数分别为-1和 ,
∴点B到点A的距离为1+ ,则点 C 到点 A 的距离为1+ ,
设点C表示的实数为x,则点A到点C的距离为-1-x,
∴-1-x=1+ ,
∴ x=-2-
方法总结
本题主要考查了实数与数轴之间的对应关系,其中利用了:当点 C 为点 B 关于点 A 的对称点时,点 C 到点 A的距离等于点 B 到点 A 的距离;
两点之间的距离为两数差的绝对值.
1 把下列各数填入相应的框内:
,,, ,,,1.3,0,18,,.
2 判断(正确的画“√”,错误的画“×”):
(1)任何一个无理数的绝对值都是正数;( )
(2)不带根号的数都是有理数;( )
(3)实数可以分为正实数和负实数两类.( )
√
×
×
3 求下列各数的相反数和绝对值:
(1);
(2) ;
(3).
(3) 的相反数是_______,绝对值是________;
1.填空.
(1)3.14的相反数是_______,绝对值是________;
(2) 的相反数是_______,绝对值是________;
-3.14
3.14
(5)点A在数轴上表示的数为 ,点B在数轴上对应的数为 ,则A,B两点的距离为_________.
(4) 的相反数是__________,绝对值是___________;
2.如图,在数轴上点A和点B之间的整数是 .
【解析】1< <2,2< <3,在 与 之间的整数是2.
A
B
2
同课章节目录
