2.3.2 实数的运算 课件(共37张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 2.3.2 实数的运算 课件(共37张PPT)2024-2025学年数学湘教版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 35.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 16:23:05 | ||
图片预览











文档简介
(共37张PPT)
2.3 实数
2.3.2 实数的运算
有理数可以做加、减、乘、除、乘方运算,实数可以吗?
把数从有理数扩充到实数以后,实数也可以进行加、减、乘、除、乘方运算,而且非负数可以进行开平方运算,任意实数都可以进行开立方运算.
在进行实数的运算时,有理数的运算法则、运算律等,对于实数仍然成立.
前面所学的有关数、式、方程(组)的性质、法则和解法,对于实数仍然成立.
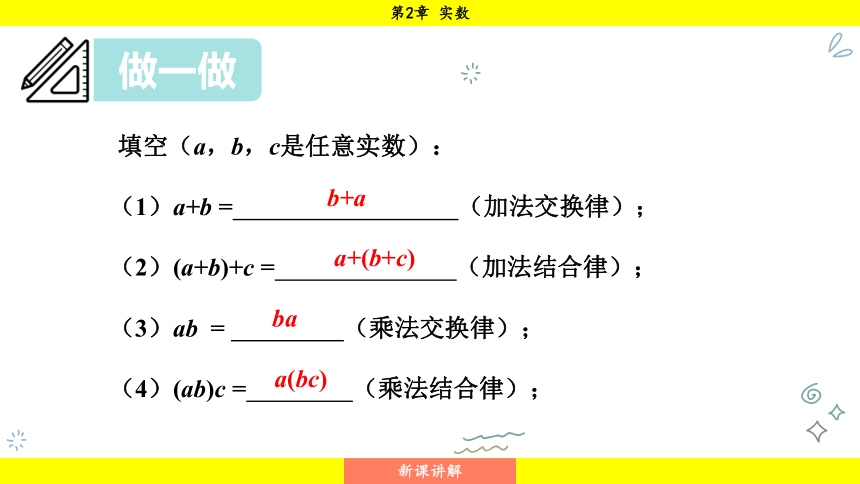
填空(a,b,c是任意实数):
(1)a+b = (加法交换律);
(2)(a+b)+c = (加法结合律);
(3)ab = (乘法交换律);
(4)(ab)c = (乘法结合律);
b+a
a+(b+c)
ba
a(bc)
(5)a(b+c) = (乘法对加法的分配律),
(b+c)a = (乘法对加法的分配律);
(6)实数的减法运算规定为a-b = a+ ;
(7)实数的除法运算规定为a÷b =a· (b≠0);
(8)如果a ≠ 0,b ≠ 0,那么ab 0;
ab+ac
ba+ca
(-b)
≠
(9)若ab=0,则a= 或b= .
0
0
解:
加法结合律
乘法对于加法的分配律
计算下列各式的值:
对于实数a,它有几个平方根,几个立方根呢?
在实数范围内,每个正实数a有且只有两个平方根,分别为±,且它们互为相反数,其中是a的算术平方根;
0的平方根是0;
负实数没有平方根.
当a为非负实数时,
根据平方根的定义得() =a,(-)2=a.
设a是非零实数,
由于(-a) =a ,因此a和-a是a 的两个平方根.
每个实数a有且只有一个立方根,记作,且()3=a.
★ 每个正实数有且只有两个平方根,它们互为相反数;
★ 0的平方根是0;
★ 在实数范围内,负实数没有平方根;
★ 在实数范围内,每个实数有且只有一个立方根.
实数也可以比较大小.对于实数a,b:
若a-b>0,则称a大于b(或者b小于a),记作a>b(或b若a-b<0,则称a小于b(或者b大于a),记作aa);
若a-b=0,则称a等于b,记作a=b.
要注意的是,对于任何实数a,b,
在a>b,a=b,a对于实数有:正实数大于一切负实数;两个负实数,绝对值大的数反而小;数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
一般地,对于两个正实数a,b,
若a>b,则> ,反过来也成立.
对于两个正实数a,b,
若a>b,则>,反过来也成立.
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
例2 比较下列各组数的大小.
(1)2.5 与 ; (2)3 与 ; (3)-3 与 -.
解(1)因为2.5 =6.25,() =7,又6.25<7,所以2.5<.
(2)因为33=27,()3=25,又27>25,所以3>.
(3)因为|-3|= 3,|-|=,由(2)知3>,所以-3< -.
,2可以看作分别是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此.
同样,因为5<9,所以<3.
不用计算器, 与2比较哪个大?与3比较呢?
在进行实数的计算时,有时需要估计实数的范围或者按一定的精确度求结果的近似值.
不用计算器,分别估计与在哪两个相邻整数之间.
由于10 =100<115,() =115,11 =121>115,
所以应介于10和11之间,即10<<11.
由于43=64<121,()3=121,53=125>121,
所以应介于4和5之间,即4<<5.
计算(结果保留小数点后两位):
【方法总结】在实数运算中,如果遇到无理数,并且需要求出结果的近似值时,可按要求的精确度用相应的近似有限小数代替无理数,再进行计算.
例3 用计算器计算:2× (结果精确到0.01).
解: 依次按键:
显示结果:4.472135955.
所以 2× ≈ 4.47.
在实数的运算中,
当遇到无理数并且要求出结果的近似值时,
可以按照精确度用相应的近似有限小数
(一般比计算结果要求的精确度多保留一位)
去代替无理数进行计算,
最后再四舍五入.
例4 利用 = 1.414213562…和 = 2.645751311…计算+的值(结果精确到0.001).
解 由于需精确到0.001,
于是只需取 ≈ 1.4142, ≈ 2.6457,
故+ ≈ 1.4142+2.6457 =4.0599 ≈4.060.
1 比较 -2 与-的大小.
2 不用计算器,分别估计与在哪两个相邻整数之间.
3 利用=1.259921049…和=2.236067977…计算+的值(结
果精确到0.001).
1.在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
2.估计位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
C
熟记一些常见数的算术平方根;或用计算器估计.
3.比较下列各组数的大小:
解 : (1)因为 12 < 42,
所以 < 4,
所以 < 3;
(2)因为 10 > 32 ,
所以
所以
与 3 ; (2)3.
4. 计算:
解:(1) 原式 = 4 ;
(2) 原式 = 2 .
5. 用计算器计算(精确到0.01):
(1) ; (2)1 ; (3)π .
解:(1)
(2)
(3)
6. 估计 与 6 的大小.
解:∵ 62=36<37
∴
7.计算:
(1)2+353
(2)∣2 ∣+ ∣
(3)∣ ∣+
3
2.3 实数
2.3.2 实数的运算
有理数可以做加、减、乘、除、乘方运算,实数可以吗?
把数从有理数扩充到实数以后,实数也可以进行加、减、乘、除、乘方运算,而且非负数可以进行开平方运算,任意实数都可以进行开立方运算.
在进行实数的运算时,有理数的运算法则、运算律等,对于实数仍然成立.
前面所学的有关数、式、方程(组)的性质、法则和解法,对于实数仍然成立.
填空(a,b,c是任意实数):
(1)a+b = (加法交换律);
(2)(a+b)+c = (加法结合律);
(3)ab = (乘法交换律);
(4)(ab)c = (乘法结合律);
b+a
a+(b+c)
ba
a(bc)
(5)a(b+c) = (乘法对加法的分配律),
(b+c)a = (乘法对加法的分配律);
(6)实数的减法运算规定为a-b = a+ ;
(7)实数的除法运算规定为a÷b =a· (b≠0);
(8)如果a ≠ 0,b ≠ 0,那么ab 0;
ab+ac
ba+ca
(-b)
≠
(9)若ab=0,则a= 或b= .
0
0
解:
加法结合律
乘法对于加法的分配律
计算下列各式的值:
对于实数a,它有几个平方根,几个立方根呢?
在实数范围内,每个正实数a有且只有两个平方根,分别为±,且它们互为相反数,其中是a的算术平方根;
0的平方根是0;
负实数没有平方根.
当a为非负实数时,
根据平方根的定义得() =a,(-)2=a.
设a是非零实数,
由于(-a) =a ,因此a和-a是a 的两个平方根.
每个实数a有且只有一个立方根,记作,且()3=a.
★ 每个正实数有且只有两个平方根,它们互为相反数;
★ 0的平方根是0;
★ 在实数范围内,负实数没有平方根;
★ 在实数范围内,每个实数有且只有一个立方根.
实数也可以比较大小.对于实数a,b:
若a-b>0,则称a大于b(或者b小于a),记作a>b(或b
若a-b=0,则称a等于b,记作a=b.
要注意的是,对于任何实数a,b,
在a>b,a=b,a
原点
0
正实数
负实数
<
一般地,对于两个正实数a,b,
若a>b,则> ,反过来也成立.
对于两个正实数a,b,
若a>b,则>,反过来也成立.
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
例2 比较下列各组数的大小.
(1)2.5 与 ; (2)3 与 ; (3)-3 与 -.
解(1)因为2.5 =6.25,() =7,又6.25<7,所以2.5<.
(2)因为33=27,()3=25,又27>25,所以3>.
(3)因为|-3|= 3,|-|=,由(2)知3>,所以-3< -.
,2可以看作分别是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此.
同样,因为5<9,所以<3.
不用计算器, 与2比较哪个大?与3比较呢?
在进行实数的计算时,有时需要估计实数的范围或者按一定的精确度求结果的近似值.
不用计算器,分别估计与在哪两个相邻整数之间.
由于10 =100<115,() =115,11 =121>115,
所以应介于10和11之间,即10<<11.
由于43=64<121,()3=121,53=125>121,
所以应介于4和5之间,即4<<5.
计算(结果保留小数点后两位):
【方法总结】在实数运算中,如果遇到无理数,并且需要求出结果的近似值时,可按要求的精确度用相应的近似有限小数代替无理数,再进行计算.
例3 用计算器计算:2× (结果精确到0.01).
解: 依次按键:
显示结果:4.472135955.
所以 2× ≈ 4.47.
在实数的运算中,
当遇到无理数并且要求出结果的近似值时,
可以按照精确度用相应的近似有限小数
(一般比计算结果要求的精确度多保留一位)
去代替无理数进行计算,
最后再四舍五入.
例4 利用 = 1.414213562…和 = 2.645751311…计算+的值(结果精确到0.001).
解 由于需精确到0.001,
于是只需取 ≈ 1.4142, ≈ 2.6457,
故+ ≈ 1.4142+2.6457 =4.0599 ≈4.060.
1 比较 -2 与-的大小.
2 不用计算器,分别估计与在哪两个相邻整数之间.
3 利用=1.259921049…和=2.236067977…计算+的值(结
果精确到0.001).
1.在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
2.估计位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
C
熟记一些常见数的算术平方根;或用计算器估计.
3.比较下列各组数的大小:
解 : (1)因为 12 < 42,
所以 < 4,
所以 < 3;
(2)因为 10 > 32 ,
所以
所以
与 3 ; (2)3.
4. 计算:
解:(1) 原式 = 4 ;
(2) 原式 = 2 .
5. 用计算器计算(精确到0.01):
(1) ; (2)1 ; (3)π .
解:(1)
(2)
(3)
6. 估计 与 6 的大小.
解:∵ 62=36<37
∴
7.计算:
(1)2+353
(2)∣2 ∣+ ∣
(3)∣ ∣+
3
同课章节目录
