《我变胖了》

课件18张PPT。 欢迎大家光临三疑三探课堂杨 彦 平
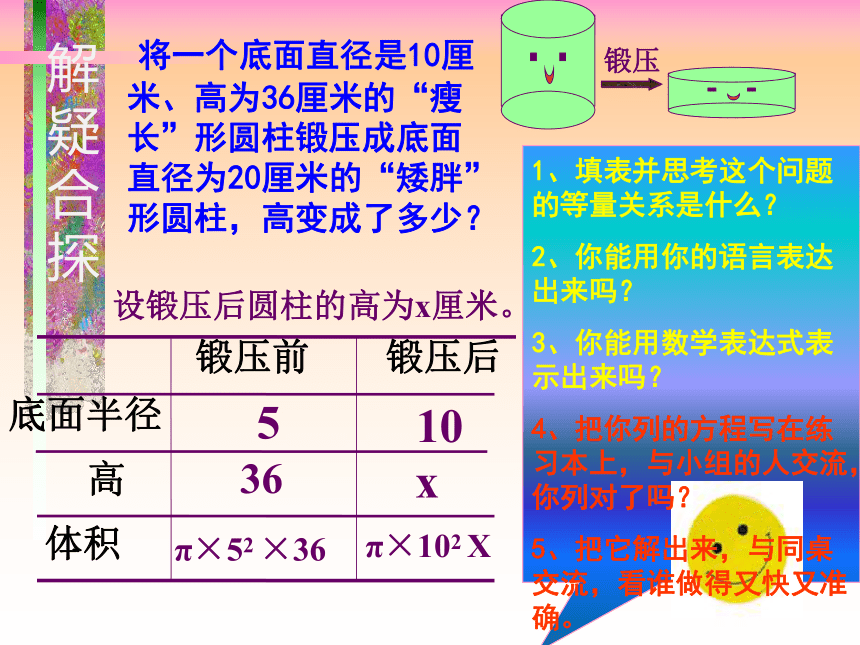
2009、11、26知 识 复 习长方形的周长 l=_______，面积S=_______，2(a+b)ab长方体体积V=_________。abc正方形的周长 l=_______，面积S=_______，4aa2正方体体积V=______。a3圆的周长l =________，面积S=_______，圆柱体体积V=_________。温故知新朝三暮四的故事 从前有一个叫狙公的人养了一群猴子。每天他都拿足够的栗子给猴子吃，猴子高兴，他也快乐。有一天他发现如果再这样喂猴子的话，等不到下一个栗子的收获季节，他的猴子都会饿死。于是他想了一个办法，并且把这个办法说给猴子听，当猴子听到只能早上吃四个，晚上吃三个栗子时很是生气，呲牙咧嘴的。没办法，狙公只好说早上吃三个，晚上吃四个，没想到猴子一听高兴的直打筋斗。 新课引入3+4＝4+3把手里的橡皮泥压一压，在手压前和手压后有何变化？ 你发现了一个相等关系没有？能用自己的话告诉大家吗？设疑自探设疑自探5.4 我变胖了1、 猜一猜 我是怎么变胖的？ 2、 哪些量改变了？锻压3、哪些量没变？（底面半径、 高改变了） （体积 、重量）设疑自探 将一个底面直径是10厘米、高为36厘米的“瘦长”形圆柱锻压成底面直径为20厘米的“矮胖”形圆柱，高变成了多少？
设锻压后圆柱的高为x厘米。1036π×52 ×36π×102 X5x解疑合探因此，高变成了 厘米 锻压前的体积=锻压后的体积解：设锻压后圆柱的高为x厘米。
根据等量关系，列出方程： × 52×36 × 102 × x解得： X=9等量关系： 列方程解决实际问题的关键是正确找出等量关系。=9解疑合探 质疑再探把一根铁丝围成一个长方形，有多少种围法？它们的周长改变了吗？它们的面积都相等吗？不论图形的形状如何变化，它的周长始终是不变的。
观察与思考例1、（1） 用一根长为10米的铁丝围成一个长方形，使得该长方形的长比宽多1.4米，此时长方形的长、宽各是多少米呢？面积是多少？质疑再探解： 设长方形的宽为X米，则它的 长为 (X+1.4)米。根据题意得：(X+1.4 +X) ×2 =10解得：X=1.8 此时长方形的长为3.2米，宽为1.8米, 面积是5.76米2.分析：
（长+宽）× 2=周长面积： 3.2 × 1.8=5.76（米2 ）1.8+1.4=3.2
（2）使长方形的长比宽多0.8米，此时长方形的长、宽各为多少米？它所围成的长方形与第一次所围成的长方形相比，面积有什么变化？解：（1）设长方形的宽为x米，则它的长为（x+0.8）米。
根据题意，得：(X+0.8 +X) ×2 =10解得：x=2.1面积：2.9 ×2.1=6.09(米2)长为：2.1+0.8=2.9（米）自己解例题面积增大： 6. 09 -5.76=0.33(米2)
（3）若使长方形的长和宽相等，即围成一个正方形，此时正方形的边长是多少米？围成的面积与前两次围成的面积相比，又有什么变化？解：设正方形的边长为x米。
根据题意，得：解得：x=2.54x =10面积：2.5 × 2.5 =6. 25(米2)面积增大： 6. 25 -6.09=0.16(米2)比比赛赛解例题同样长的铁丝围成怎样的四边形面积最大呢？面积：1.8 × 3.2=5.76面积:2.9 ×2.1=6.09面积:2.5 2=6. 25质疑再探学以致用 若小明用10米铁线在墙边围成一个长方形鸡棚，使长比宽大5米，但在宽的一边有一扇1米宽的门，那么，请问小明围成的鸡棚的长和宽又是多少呢？门墙面铁线拓展运用帮一帮谈谈你的收获6、应用方程解决问题的一般步骤：
审、设、找、列、解、检、答 本节课你学会了什么？3、列方程的关键是正确找出等量关系 5、长方形周长不变时，长方形的面积随着长与宽的变化而变化，当长与宽相等时(即正方形)，面积最大1、等体积变化：
锻压前体积 = 锻压后体积
锻压前重量 = 锻压后重量4、线段长度一定时，不管围成怎样的图形，周长不变。2、等周长变形：变形前周长 ＝ 变形后周长
1、Ｐ186习题5.7　1、2、。
2、阅读教材Ｐ184　“读一读”， 看后写一篇体会.布 置 作 业