5.2 简单的轴对称图形 课件(共43张PPT)2024-2025学年数学北师大版七年级下册
文档属性
| 名称 | 5.2 简单的轴对称图形 课件(共43张PPT)2024-2025学年数学北师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 17:34:07 | ||
图片预览











文档简介
(共43张PPT)
轴对称及其性质
轴对称现象
轴对称的性质
定义
区别
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
轴对称图形:一个图形具有的特殊形状.
成轴对称:两个全等图形的特殊的位置关系.
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等,对应角相等
观察下列图片,它们有什么共同的特征?
等腰三角形
(1)等腰三角形是轴对称图形吗
如果是,沿它的对称轴折叠
你能发现哪些相等的线段和相等的角
(2)等腰三角形的对称轴是一条怎样的直线
你是如何描述的
(3)你认为等腰三角形有哪些特征 与同伴进行交流
等腰三角形是轴对称图形等腰三角形
顶角的平分线、底边上的中线、底边上的高重合
也称“三线合一”
它们所在的直线是等腰三角形的对称轴。
等腰三角形的两个底角相等
例1 已知一个等腰三角形的底角是顶角的2倍,求它的各个内角的度数。
解:设这个等腰三角形顶角的度数为x
则底角的度数为2x
根据“三角形三个内角的和等于180°”,
得x+2x+2x=180
解得 x=36
2×36=72
所以,这个三角形的三个内角分别是36°,72°,72 °
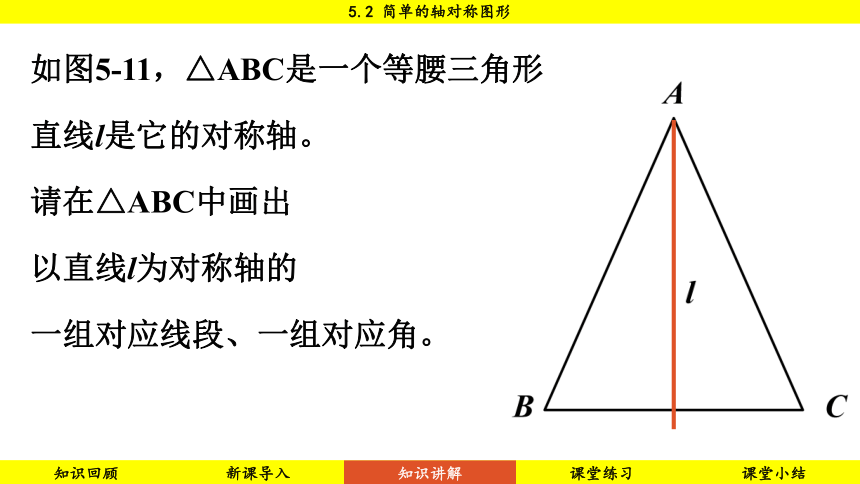
如图5-11,△ABC是一个等腰三角形
直线l是它的对称轴。
请在△ABC中画出
以直线l为对称轴的
一组对应线段、一组对应角。
你能发现哪些相等的线段、相等的角,以及形状、大小完全相同的图形?
(1)等边三角形有几条对称轴
(2)你能发现它的哪些特征
与同伴进行交流。
1.下面是由大小不同的等边三角形组成的图案,请找出它的对称轴。
2.墙上钉了一根木条,李叔叔想用一个如图所示的测平仪检验这根木条是否水平。
在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤李叔叔将 BC边与木条重合,观察此时重垂线是否通过点A。如果重垂线过点4,那么这根木条就是水平的。请说明其中的道理。
线段(如图5-12)是轴对称图形吗
如果是,请描述它的对称轴的特点。
线段是轴对称图形,
垂直并且平分线段的直线
是它的一条对称轴
垂直于一条线段
并且平分这条线段的直线
叫作这条线段的垂直平分线简称中垂线
如图5-13,直线l是线段AB的垂直点
C是l上的任意一点。
在线段AB上画出
以l为对称轴的一组对应点D和D',
连接CD和CD'
(1)你认为线段 CD和CD'之间有什么关系 说说你的理由
(2)特别地,当点 D与点A重合时,点 D'位于什么位置
此时,线段 CD 和 CD'之间还有(1)中的关系吗
由此你能得到什么结论
线段垂直平分线上的点
到这条线段两个端点的距离相等
如图5-14,已师线段 AB,如何作出它的垂直平分线
假设线段AB的乘直平分线已作出,请回答下列问题
(1)这条直线有什么特征
(2)如何确定这条直线上的两个点 用三角尺、量角器、圆规等工具试一试。如果只用尺规呢 与同伴进行交流。
例2 如图5-15,已知线段 AB,
请用尺规作图
线段 AB的垂直平分线
作法:1.分别以点A和点B为圆心,以大于亏AB的长为半径作弧,两弧相交于点C和D(如图5-15)。
2.作直线CD
直线CD就是线段AB的垂直平分线
如图5-16,已知直线l和l上的一点P,如何用尺规作l的垂线,使它经过点P
能说明你的作法的道理吗
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED的长是多少?
2.画一条线段PQ,用尺规作线段PQ的中点
P
Q
角是生活中常见的图形。
角是轴对称图形吗
如果是
请指出它的对称轴。
角是轴对称图形
角平分线听在的直线是它的对称轴
如图5-19,OP是∠AOB的平分线,点C是OP上的任意一点。在∠AOB的两边上画出以OP所在直线为对称轴的一组对应点D和D’,连接 CD和 CD ’
(1)你认为线段CD和CD'之间有什么关系 说说你的理由。
当 CD⊥OA 时,OD’与OB有怎样的关系?
为什么?
此时,线段CD和CD’之间还有(1)中的关系吗?
由此你能得到什么结论?
角平分线上的点到这个角的两边的距离相等
如图,已知∠AOB,如何作出它的平分线
O
A
B
假设∠AOB的平分线已作出,请回答下列问题:
(1)这条射线有什么特征
(2)如何确定这条射线上除端点之外的一个点
用三角尺、量角器、圆规等行交流
如果只用尺规呢?
与同伴进行交流。
例3 如图,已知∠AOB,请用尺规作>4OB的平分线。
作法:
1.在A和OB上分别截取OD,OE
使OD=OE(如图)
2.分别以点D和点E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内相交于点C
3.作射线OC
射线OC就是∠AOB的平分线
过直线上一点作已知直线的垂线与作一个平角的平分线,这两种规作图方法有什么共同点
与同伴进行交流。
回顾研究等腰三角形、线段、角的过程,你运用了哪些方法 积累了哪些经验
1.如图所示,在Rt△ABC中,BD是∠ABC的平分线
DE⊥AB,垂足为E.
DE与DC相等吗 为什么
先任意画一个角,然后将它四等分
简单的轴对称图形
等腰三角形的性质
线段垂直平分线的性质
角平分线
等腰三角形等边对等角.
等腰三角形三线合一
内容:线段垂直平分线上的点到线段的两个端点的距离相等
作用:见垂直平分线,得线段相等
尺规作图
属于基本作图,须熟练掌握
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
轴对称及其性质
轴对称现象
轴对称的性质
定义
区别
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴.
轴对称图形:一个图形具有的特殊形状.
成轴对称:两个全等图形的特殊的位置关系.
1.对应点所连的线段被对称轴垂直平分
2.对应线段相等,对应角相等
观察下列图片,它们有什么共同的特征?
等腰三角形
(1)等腰三角形是轴对称图形吗
如果是,沿它的对称轴折叠
你能发现哪些相等的线段和相等的角
(2)等腰三角形的对称轴是一条怎样的直线
你是如何描述的
(3)你认为等腰三角形有哪些特征 与同伴进行交流
等腰三角形是轴对称图形等腰三角形
顶角的平分线、底边上的中线、底边上的高重合
也称“三线合一”
它们所在的直线是等腰三角形的对称轴。
等腰三角形的两个底角相等
例1 已知一个等腰三角形的底角是顶角的2倍,求它的各个内角的度数。
解:设这个等腰三角形顶角的度数为x
则底角的度数为2x
根据“三角形三个内角的和等于180°”,
得x+2x+2x=180
解得 x=36
2×36=72
所以,这个三角形的三个内角分别是36°,72°,72 °
如图5-11,△ABC是一个等腰三角形
直线l是它的对称轴。
请在△ABC中画出
以直线l为对称轴的
一组对应线段、一组对应角。
你能发现哪些相等的线段、相等的角,以及形状、大小完全相同的图形?
(1)等边三角形有几条对称轴
(2)你能发现它的哪些特征
与同伴进行交流。
1.下面是由大小不同的等边三角形组成的图案,请找出它的对称轴。
2.墙上钉了一根木条,李叔叔想用一个如图所示的测平仪检验这根木条是否水平。
在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤李叔叔将 BC边与木条重合,观察此时重垂线是否通过点A。如果重垂线过点4,那么这根木条就是水平的。请说明其中的道理。
线段(如图5-12)是轴对称图形吗
如果是,请描述它的对称轴的特点。
线段是轴对称图形,
垂直并且平分线段的直线
是它的一条对称轴
垂直于一条线段
并且平分这条线段的直线
叫作这条线段的垂直平分线简称中垂线
如图5-13,直线l是线段AB的垂直点
C是l上的任意一点。
在线段AB上画出
以l为对称轴的一组对应点D和D',
连接CD和CD'
(1)你认为线段 CD和CD'之间有什么关系 说说你的理由
(2)特别地,当点 D与点A重合时,点 D'位于什么位置
此时,线段 CD 和 CD'之间还有(1)中的关系吗
由此你能得到什么结论
线段垂直平分线上的点
到这条线段两个端点的距离相等
如图5-14,已师线段 AB,如何作出它的垂直平分线
假设线段AB的乘直平分线已作出,请回答下列问题
(1)这条直线有什么特征
(2)如何确定这条直线上的两个点 用三角尺、量角器、圆规等工具试一试。如果只用尺规呢 与同伴进行交流。
例2 如图5-15,已知线段 AB,
请用尺规作图
线段 AB的垂直平分线
作法:1.分别以点A和点B为圆心,以大于亏AB的长为半径作弧,两弧相交于点C和D(如图5-15)。
2.作直线CD
直线CD就是线段AB的垂直平分线
如图5-16,已知直线l和l上的一点P,如何用尺规作l的垂线,使它经过点P
能说明你的作法的道理吗
1.如图,已知AB是线段CD的垂直平分线,E是AB上的一点,如果EC=7cm,那么ED的长是多少?
2.画一条线段PQ,用尺规作线段PQ的中点
P
Q
角是生活中常见的图形。
角是轴对称图形吗
如果是
请指出它的对称轴。
角是轴对称图形
角平分线听在的直线是它的对称轴
如图5-19,OP是∠AOB的平分线,点C是OP上的任意一点。在∠AOB的两边上画出以OP所在直线为对称轴的一组对应点D和D’,连接 CD和 CD ’
(1)你认为线段CD和CD'之间有什么关系 说说你的理由。
当 CD⊥OA 时,OD’与OB有怎样的关系?
为什么?
此时,线段CD和CD’之间还有(1)中的关系吗?
由此你能得到什么结论?
角平分线上的点到这个角的两边的距离相等
如图,已知∠AOB,如何作出它的平分线
O
A
B
假设∠AOB的平分线已作出,请回答下列问题:
(1)这条射线有什么特征
(2)如何确定这条射线上除端点之外的一个点
用三角尺、量角器、圆规等行交流
如果只用尺规呢?
与同伴进行交流。
例3 如图,已知∠AOB,请用尺规作>4OB的平分线。
作法:
1.在A和OB上分别截取OD,OE
使OD=OE(如图)
2.分别以点D和点E为圆心,以大于DE的长为半径作弧,两弧在∠AOB内相交于点C
3.作射线OC
射线OC就是∠AOB的平分线
过直线上一点作已知直线的垂线与作一个平角的平分线,这两种规作图方法有什么共同点
与同伴进行交流。
回顾研究等腰三角形、线段、角的过程,你运用了哪些方法 积累了哪些经验
1.如图所示,在Rt△ABC中,BD是∠ABC的平分线
DE⊥AB,垂足为E.
DE与DC相等吗 为什么
先任意画一个角,然后将它四等分
简单的轴对称图形
等腰三角形的性质
线段垂直平分线的性质
角平分线
等腰三角形等边对等角.
等腰三角形三线合一
内容:线段垂直平分线上的点到线段的两个端点的距离相等
作用:见垂直平分线,得线段相等
尺规作图
属于基本作图,须熟练掌握
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
同课章节目录
