7.2 不等式的基本性质 课件(共34张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 7.2 不等式的基本性质 课件(共34张PPT)2024-2025学年数学华师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 912.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 22:14:34 | ||
图片预览









文档简介
(共34张PPT)
7.2 不等式的基本性质
不等式的解集
在数轴上表示
不等式解集的表示
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集
概念
在解一元一次方程时,我们根据等式的基本性质对方程进行变形.
等式的基本性质 1:等式两边都加上(或都减去)同一个数或同一个整式,所得结果仍是等式.
等式的基本性质 2:等式两边都乘以(或都除以)同一个数(除数不能为0),所得结果仍是等式.
等式有哪些基本性质?
在研究解不等式时,我们需要认识不等式的基本性质.
等式的这些性质适用于不等式吗?
不等式有哪些性质呢?
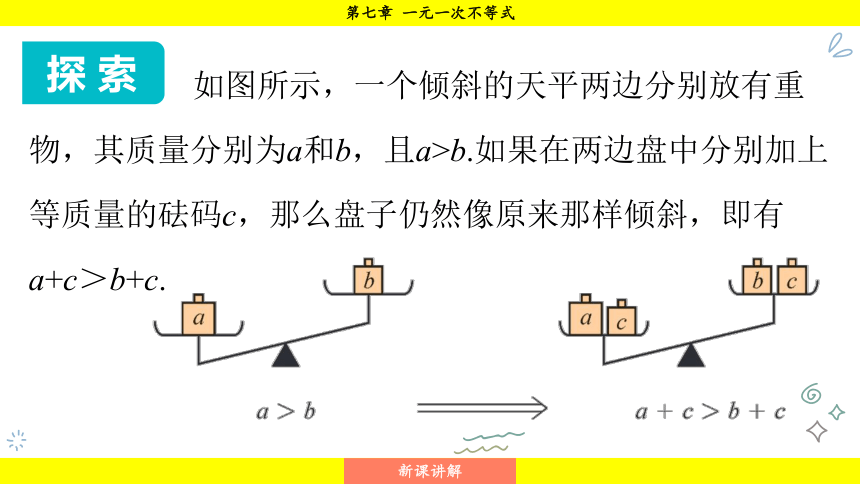
如图所示,一个倾斜的天平两边分别放有重物,其质量分别为a和b,且a>b.如果在两边盘中分别加上等质量的砝码c,那么盘子仍然像原来那样倾斜,即有a+c>b+c.
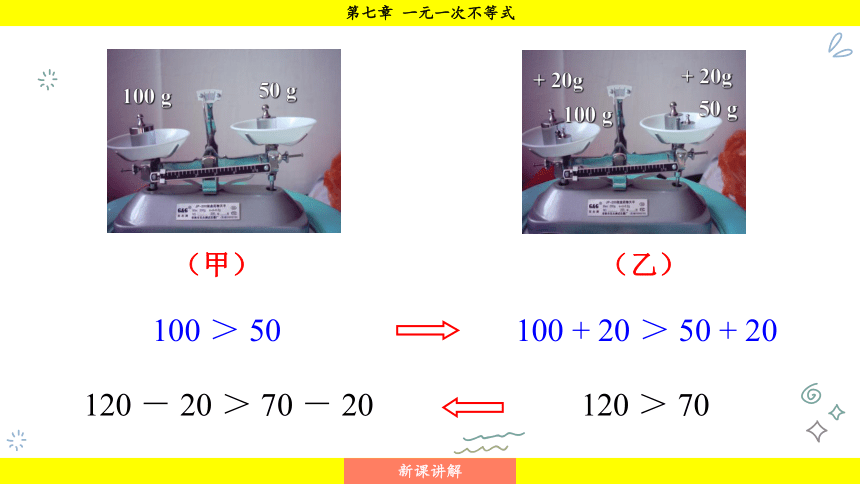
(甲)
(乙)
100 g
50 g
100 > 50
100 + 20 > 50 + 20
120 > 70
120 - 20 > 70 - 20
+ 20g
+ 20g
100 g
50 g
不等式的基本性质1
如果 a > b ,那么
a + c > b + c ,a – c > b – c .
这就是说,不等式的两边都加上(或都减去)同一个数,不等号的方向不变.
1.用“>”或“<”填空.
(1) 5 > 3,5+2 ___ 3+2,5-2 ___ 3-2;
(2) -1 < 3,-1+2 ___ 3+2 ,-1-3 ___ 3-3.
>
>
<
<
不等式的两边都乘以(或都除以)同一个不为0的数,不等号的方向是否也不变呢?
将不等式 7 > 4 的两边都乘以同一个数,例如3、2、1、0、-1、-2、-3,比较所得结果的大小,用“<”“>”或“=”填空:
从中你能发现什么?
不等式的基本性质2
如果 a > b ,并且 c > 0 ,那么
ac > bc , > .
这就是说,不等式的两边都乘以(或都除以)同一个正数,不等号的方向不变.
不等式的基本性质3
如果 a > b ,并且 c < 0 ,那么
ac < bc , < .
不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
2.用“>”或“<”填空.
(1) 6>2, 6×5 ____ 2×5, 6×(-5)____ 2×(-5);
(2) -2<3, (-2)×6____3×6, (-2)×(-6)____3×(-6).
>
<
<
>
3. 设 a>b,用“<”“>”填空,并回答是根据不等式
的哪一条基本性质.
(1) a-3 ____ b-3;
(2) a÷3 ____ b÷3;
(3) 0.1a ____ 0.1b;
>
>
>
不等式的性质 1
不等式的性质 2
不等式的性质 2
(4) -4a ____ -4b;
(5) 2a+3 ____ 2b+3;
(6) (m2+1)a ____ (m2+1)b (m 为常数)
>
>
<
不等式的性质 3
不等式的性质 1,2
不等式的性质 2
4. 已知 a<0,用“<”“>”填空:
(1) a + 2 ____ 2; (2) a - 1 _____-1;
(3) 3a _____ 0; (4) ____ 0;
(5) a2 ____ 0; (6) a3 ____ 0;
(7) a-1 ____ 0; (8) | a | ____ 0.
<
<
<
>
<
>
<
>
不等式的基本性质可以作为推理的依据.
例1 利用不等式的基本性质说明下列结论的正确性:
(1)如果 a – b > 0 ,那么 a > b ;
(2)如果 a – b < 0 ,那么 a < b .
解(1)因为 a – b > 0 ,将不等式的两边都加上 b ,由不等式的基本性质1可得
a – b + b > 0 + b ,
所以 a > b .
(2)因为 a – b < 0 ,将不等式的两边都加上 b ,由不等式的基本性质1,可得
a – b + b < 0 + b ,
所以 a < b .
交换例1中两道小题的条件和结论,其正确性不变,即
如果 a > b ,那么 a – b > 0 ;
如果 a < b ,那么 a – b < 0 .
由此可见, a > b 与 a – b > 0 、 a < b 与 a – b < 0 可以相互转化.因此,要较 a 与 b 的大小,只需要比较 a – b 与0的大小.
试说明这两个结论的正确性.
例2 利用不等式的基本性质说明下列结论的正确性:
(1)如果 a > b ,c > d ,那么 a + c > b + d ;
(2)如果 a、b、c、d 都是正数,且 a > b,c > d ,那么 ac > bd .
解(1)因为 a > b ,所以
a + c > b + c . ①
又因为 c > d ,所以
b + c > b + d . ②
由①②,可得
a + c > b + d .
由数的大小比较可知,不等关系具有传递性,即如果 a > b 且 b > c ,那么 a > c .它也可以作为推理的依据.
(2)因为 a > b ,c 是正数,所以
ac > bc. ①
又因为 c > d ,b 是正数,所以
bc > bd . ②
由①②,可得
ac > bd .
1.说出下列不等式变形的依据:
(1)由 x – 2 > 0 ,得 x > 2 ;
(2)由1 - 2x ≤ 0 ,得 x ≥ .
2.利用不等式的基本性质说明下列结论的正确性:
(1)一个数加上一个正数比这个数大;
(2)一个数加上一个负数比这个数小.
3.一个正数乘以一个数,一定比这个正数大吗?为什么?
1. 已知 a<b,用“>”或“<” 填空:
(1) a+12 b+12;
(2) b-10 a-10.
2. 把下列不等式化为 x > a 或 x < a 的形式:
(1) 5>3+x;
(2) 2x<x+6.
<
>
解:x<2.
解:x<6.
不等式的基本性质
不等式的基本性质 2
不等式的基本性质 3
不等式的基本性质 1
不等式的基本性质 1
如果 a > b ,那么
a + c > b + c ,a – c > b – c .
不等式的两边都加上(或都减去)同一个数,不等号的方向不变.
不等式的基本性质 2
如果 a > b ,并且 c > 0 ,那么
ac > bc , > .
不等式的两边都乘以(或都除以)同一个正数,不等号的方向不变.
不等式的基本性质 3
如果 a > b ,并且 c < 0 ,那么
ac < bc , < .
不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
7.2 不等式的基本性质
不等式的解集
在数轴上表示
不等式解集的表示
一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集
概念
在解一元一次方程时,我们根据等式的基本性质对方程进行变形.
等式的基本性质 1:等式两边都加上(或都减去)同一个数或同一个整式,所得结果仍是等式.
等式的基本性质 2:等式两边都乘以(或都除以)同一个数(除数不能为0),所得结果仍是等式.
等式有哪些基本性质?
在研究解不等式时,我们需要认识不等式的基本性质.
等式的这些性质适用于不等式吗?
不等式有哪些性质呢?
如图所示,一个倾斜的天平两边分别放有重物,其质量分别为a和b,且a>b.如果在两边盘中分别加上等质量的砝码c,那么盘子仍然像原来那样倾斜,即有a+c>b+c.
(甲)
(乙)
100 g
50 g
100 > 50
100 + 20 > 50 + 20
120 > 70
120 - 20 > 70 - 20
+ 20g
+ 20g
100 g
50 g
不等式的基本性质1
如果 a > b ,那么
a + c > b + c ,a – c > b – c .
这就是说,不等式的两边都加上(或都减去)同一个数,不等号的方向不变.
1.用“>”或“<”填空.
(1) 5 > 3,5+2 ___ 3+2,5-2 ___ 3-2;
(2) -1 < 3,-1+2 ___ 3+2 ,-1-3 ___ 3-3.
>
>
<
<
不等式的两边都乘以(或都除以)同一个不为0的数,不等号的方向是否也不变呢?
将不等式 7 > 4 的两边都乘以同一个数,例如3、2、1、0、-1、-2、-3,比较所得结果的大小,用“<”“>”或“=”填空:
从中你能发现什么?
不等式的基本性质2
如果 a > b ,并且 c > 0 ,那么
ac > bc , > .
这就是说,不等式的两边都乘以(或都除以)同一个正数,不等号的方向不变.
不等式的基本性质3
如果 a > b ,并且 c < 0 ,那么
ac < bc , < .
不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
2.用“>”或“<”填空.
(1) 6>2, 6×5 ____ 2×5, 6×(-5)____ 2×(-5);
(2) -2<3, (-2)×6____3×6, (-2)×(-6)____3×(-6).
>
<
<
>
3. 设 a>b,用“<”“>”填空,并回答是根据不等式
的哪一条基本性质.
(1) a-3 ____ b-3;
(2) a÷3 ____ b÷3;
(3) 0.1a ____ 0.1b;
>
>
>
不等式的性质 1
不等式的性质 2
不等式的性质 2
(4) -4a ____ -4b;
(5) 2a+3 ____ 2b+3;
(6) (m2+1)a ____ (m2+1)b (m 为常数)
>
>
<
不等式的性质 3
不等式的性质 1,2
不等式的性质 2
4. 已知 a<0,用“<”“>”填空:
(1) a + 2 ____ 2; (2) a - 1 _____-1;
(3) 3a _____ 0; (4) ____ 0;
(5) a2 ____ 0; (6) a3 ____ 0;
(7) a-1 ____ 0; (8) | a | ____ 0.
<
<
<
>
<
>
<
>
不等式的基本性质可以作为推理的依据.
例1 利用不等式的基本性质说明下列结论的正确性:
(1)如果 a – b > 0 ,那么 a > b ;
(2)如果 a – b < 0 ,那么 a < b .
解(1)因为 a – b > 0 ,将不等式的两边都加上 b ,由不等式的基本性质1可得
a – b + b > 0 + b ,
所以 a > b .
(2)因为 a – b < 0 ,将不等式的两边都加上 b ,由不等式的基本性质1,可得
a – b + b < 0 + b ,
所以 a < b .
交换例1中两道小题的条件和结论,其正确性不变,即
如果 a > b ,那么 a – b > 0 ;
如果 a < b ,那么 a – b < 0 .
由此可见, a > b 与 a – b > 0 、 a < b 与 a – b < 0 可以相互转化.因此,要较 a 与 b 的大小,只需要比较 a – b 与0的大小.
试说明这两个结论的正确性.
例2 利用不等式的基本性质说明下列结论的正确性:
(1)如果 a > b ,c > d ,那么 a + c > b + d ;
(2)如果 a、b、c、d 都是正数,且 a > b,c > d ,那么 ac > bd .
解(1)因为 a > b ,所以
a + c > b + c . ①
又因为 c > d ,所以
b + c > b + d . ②
由①②,可得
a + c > b + d .
由数的大小比较可知,不等关系具有传递性,即如果 a > b 且 b > c ,那么 a > c .它也可以作为推理的依据.
(2)因为 a > b ,c 是正数,所以
ac > bc. ①
又因为 c > d ,b 是正数,所以
bc > bd . ②
由①②,可得
ac > bd .
1.说出下列不等式变形的依据:
(1)由 x – 2 > 0 ,得 x > 2 ;
(2)由1 - 2x ≤ 0 ,得 x ≥ .
2.利用不等式的基本性质说明下列结论的正确性:
(1)一个数加上一个正数比这个数大;
(2)一个数加上一个负数比这个数小.
3.一个正数乘以一个数,一定比这个正数大吗?为什么?
1. 已知 a<b,用“>”或“<” 填空:
(1) a+12 b+12;
(2) b-10 a-10.
2. 把下列不等式化为 x > a 或 x < a 的形式:
(1) 5>3+x;
(2) 2x<x+6.
<
>
解:x<2.
解:x<6.
不等式的基本性质
不等式的基本性质 2
不等式的基本性质 3
不等式的基本性质 1
不等式的基本性质 1
如果 a > b ,那么
a + c > b + c ,a – c > b – c .
不等式的两边都加上(或都减去)同一个数,不等号的方向不变.
不等式的基本性质 2
如果 a > b ,并且 c > 0 ,那么
ac > bc , > .
不等式的两边都乘以(或都除以)同一个正数,不等号的方向不变.
不等式的基本性质 3
如果 a > b ,并且 c < 0 ,那么
ac < bc , < .
不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变.
