7.3.2 一元一次不等式的实际应用 课件(共26张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 7.3.2 一元一次不等式的实际应用 课件(共26张PPT)2024-2025学年数学华师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 22:15:08 | ||
图片预览








文档简介
(共26张PPT)
7.3 解一元一次不等式
7.3.2 一元一次不等式的实际应用
解一元一次不等式:
1.一元一次不等式的概念
只含有一个未知数、左右两边都是整式,并且未知数的次数都是1的不等式,叫做一元一次不等式.
2.解一元一次不等式的方法
与解方程类似,解不等式的过程,就是利用不等式的基本性质,将不等式进行适当的变形,得到 x > a 或 x < a的形式.
复习导入
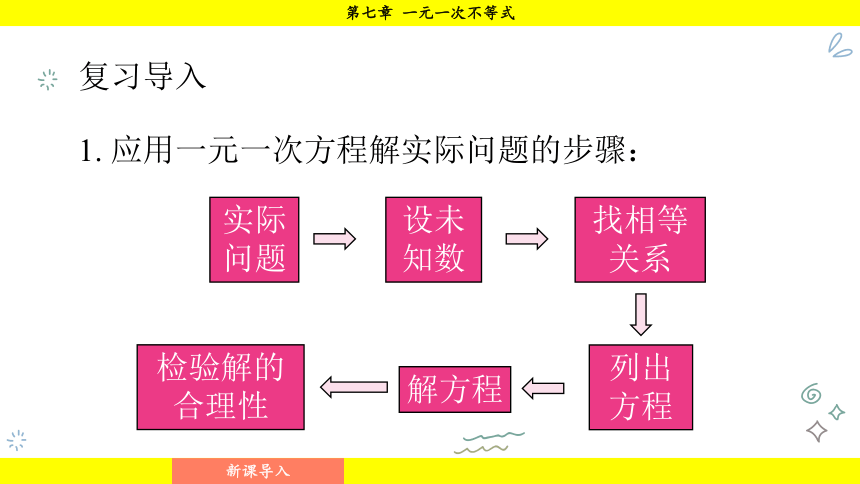
1. 应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
复习导入
2. 将下列生活中的不等关系翻译成数学语言。
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
例5 一个工程队原定在10天内至少要挖土600 m3 ,前两天一共完成了120 m3,由于整个工程调整工期,要求提前两天完成挖土任务.问:后6天内平均每天至少要挖土多少立方米?
解 设后6天内平均每天要挖土 x m3.根据题意,得
120 + 6x ≥ 600 ,
解得 x ≥ 80 .
答:后6天内平均每天至少要挖土80 m3.
问题 在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得10分,答错或不答扣5分,总得分不少于80分者能通过预选赛.育才中学有25名学生通过了预选赛,通过者至少应答对多少道题?有哪些可能情形?
(1)试解决这个问题.你是用什么方法解决的?有没有其他方法?与你的同伴讨论和交流一下.
(2)如果你是利用不等式的知识解决这个问题的,那么在得到不等式的解集后,如何给出原问题的答案?应该如何表述?
小华与同学约好去登山,计划上午 7 点出发,到达山顶后休息 2 h,最晚下午 4 点回到出发点.如果他们去时的平均速度是 3 km/h,回程是 4 km/h,他们
最远能登上哪座山顶 (图中数字
表示出发点到山顶的路程)?
前面问题中涉及的数量关系是:
去时所花时间+休息时间
+回来所花时间 ≤ 总时间.
解:设从出发点到山顶的距离为 x km,则他们去时所花
时间为 h,回来所花时间为 h.
他们在山顶休息了 2 h,又上午 7 点到下午 4 点之间总共相隔 9 h,即所用时间应小于或等于 9 h。
所以有 +2+ ≤ 9.
解得 x ≤ 12.
因此要满足最晚下午 4 点
回到出发点,小华他们最远能登上 D 山顶。
题1 某童装店按每套 90 元的价格购进 40 套童装,应缴纳的税费为销售额的 10%. 如果要获得不低于 900元的纯利润,每套童装的售价至少是多少元?
分析:本题涉及的数量关系是
销售额-成本-税费≥纯利润(900元).
解:设每套童装的售价是 x 元.
则 40x-90×40-40x·10% ≥ 900.
解得
x ≥ 125.
答:每套童装的售价至少是 125 元.
题2 当一个人坐下时,不宜提举超过 4.5 kg 的重物,以免受伤.小明坐在书桌前,桌上有两本各重 1.2 kg 的画册和一批每本重 0.4 kg 的记事本. 如果小
明想坐着搬动这两本画册和一些记事本.
问他最多只应搬动多少本记事本?
解:设小明最多只应搬动 x 本记事本,则
1.2×2+0.4x ≤ 4.5.
解得 x ≤ 5.25.
分析: 本题涉及的数量关系是
画册的总重+记事本的总重 ≤ 4.5 kg.
由于记事本的数目必须是整数,
所以 x 的最大值为 5.
答:小明最多只应搬动 5 本记事本.
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际确定答案
找出不等关系
设未知数
1.求下列不等式的所有正整数解:
(1)-4x ≥ -12 ;
(2)3x – 11 < 0 .
2.一次智力测验,有20道选择题.评分标准为:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有2道题未答,则他至少要答对几道题,总分才不会低于60分?
小明家的客厅长 5 m,宽 4 m。现在想购买边长为 60 cm 的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解:设需要购买 x 块这样的地板砖,则有
5×4 ≤ 0.6×0.6x
解得 x ≥
由于地板砖数目必须是整数,所以 x 的最小值为 56.
答:小明至少要购买 56 块地板砖。
一元一次不等式的实际应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或特殊解
↑
得出解决问题的答案
7.3 解一元一次不等式
7.3.2 一元一次不等式的实际应用
解一元一次不等式:
1.一元一次不等式的概念
只含有一个未知数、左右两边都是整式,并且未知数的次数都是1的不等式,叫做一元一次不等式.
2.解一元一次不等式的方法
与解方程类似,解不等式的过程,就是利用不等式的基本性质,将不等式进行适当的变形,得到 x > a 或 x < a的形式.
复习导入
1. 应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
复习导入
2. 将下列生活中的不等关系翻译成数学语言。
(1) 超过
(2) 至少
(3) 最多
>
≥
≤
例5 一个工程队原定在10天内至少要挖土600 m3 ,前两天一共完成了120 m3,由于整个工程调整工期,要求提前两天完成挖土任务.问:后6天内平均每天至少要挖土多少立方米?
解 设后6天内平均每天要挖土 x m3.根据题意,得
120 + 6x ≥ 600 ,
解得 x ≥ 80 .
答:后6天内平均每天至少要挖土80 m3.
问题 在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每一道题,答对得10分,答错或不答扣5分,总得分不少于80分者能通过预选赛.育才中学有25名学生通过了预选赛,通过者至少应答对多少道题?有哪些可能情形?
(1)试解决这个问题.你是用什么方法解决的?有没有其他方法?与你的同伴讨论和交流一下.
(2)如果你是利用不等式的知识解决这个问题的,那么在得到不等式的解集后,如何给出原问题的答案?应该如何表述?
小华与同学约好去登山,计划上午 7 点出发,到达山顶后休息 2 h,最晚下午 4 点回到出发点.如果他们去时的平均速度是 3 km/h,回程是 4 km/h,他们
最远能登上哪座山顶 (图中数字
表示出发点到山顶的路程)?
前面问题中涉及的数量关系是:
去时所花时间+休息时间
+回来所花时间 ≤ 总时间.
解:设从出发点到山顶的距离为 x km,则他们去时所花
时间为 h,回来所花时间为 h.
他们在山顶休息了 2 h,又上午 7 点到下午 4 点之间总共相隔 9 h,即所用时间应小于或等于 9 h。
所以有 +2+ ≤ 9.
解得 x ≤ 12.
因此要满足最晚下午 4 点
回到出发点,小华他们最远能登上 D 山顶。
题1 某童装店按每套 90 元的价格购进 40 套童装,应缴纳的税费为销售额的 10%. 如果要获得不低于 900元的纯利润,每套童装的售价至少是多少元?
分析:本题涉及的数量关系是
销售额-成本-税费≥纯利润(900元).
解:设每套童装的售价是 x 元.
则 40x-90×40-40x·10% ≥ 900.
解得
x ≥ 125.
答:每套童装的售价至少是 125 元.
题2 当一个人坐下时,不宜提举超过 4.5 kg 的重物,以免受伤.小明坐在书桌前,桌上有两本各重 1.2 kg 的画册和一批每本重 0.4 kg 的记事本. 如果小
明想坐着搬动这两本画册和一些记事本.
问他最多只应搬动多少本记事本?
解:设小明最多只应搬动 x 本记事本,则
1.2×2+0.4x ≤ 4.5.
解得 x ≤ 5.25.
分析: 本题涉及的数量关系是
画册的总重+记事本的总重 ≤ 4.5 kg.
由于记事本的数目必须是整数,
所以 x 的最大值为 5.
答:小明最多只应搬动 5 本记事本.
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际确定答案
找出不等关系
设未知数
1.求下列不等式的所有正整数解:
(1)-4x ≥ -12 ;
(2)3x – 11 < 0 .
2.一次智力测验,有20道选择题.评分标准为:对1题给5分,错1题扣2分,不答题不给分也不扣分.小明有2道题未答,则他至少要答对几道题,总分才不会低于60分?
小明家的客厅长 5 m,宽 4 m。现在想购买边长为 60 cm 的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
解:设需要购买 x 块这样的地板砖,则有
5×4 ≤ 0.6×0.6x
解得 x ≥
由于地板砖数目必须是整数,所以 x 的最小值为 56.
答:小明至少要购买 56 块地板砖。
一元一次不等式的实际应用
实际问题
↓
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或特殊解
↑
得出解决问题的答案
