8.1.1 第1课时 三角形的有关概念 课件(共47张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 8.1.1 第1课时 三角形的有关概念 课件(共47张PPT)2024-2025学年数学华师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 22:15:57 | ||
图片预览







文档简介
(共47张PPT)
8.1 与三角形有关的边和角
8.1.1 认识三角形
第1课时 三角形的有关概念
一元一次不等式组的概念
↓
↓
一元一次不等式组的解集在数轴上的表示
解一元一次不等式组
一元一次不等式组
→
一元一次不等式组的解集
↓
把未知量 x 同时满足的两个一元一次不等式合在一起,就得到一元一次不等式组.
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
一元一次不等式组的解集在数轴上的表示
埃及金字塔
水分子结构示意图
飞机机翼
问题:
(1) 从古埃及的金字塔到现代的飞机,从宏伟的建筑
物到微小的分子结构,都有什么样的形状?
(2) 在我们的生活中有没有这样的形状呢?试举例.
瓷砖是生活中常见的装饰材料。你见过哪些形状的瓷砖?它们的形状有什么特点呢?
你知道瓷砖能铺满地面的奥秘吗?
本章将在探索与三角形有关的线段和角的基础上,研究多边形的有关性质,解开关于瓷砖铺设的一个个疑团,从中了解一些研究几何问题的基本思路和方法.
走在大街上,进入宾馆或饭店,在许多地方,我们经常可以看到由各种形状的瓷砖铺成的漂亮的地面和墙面,
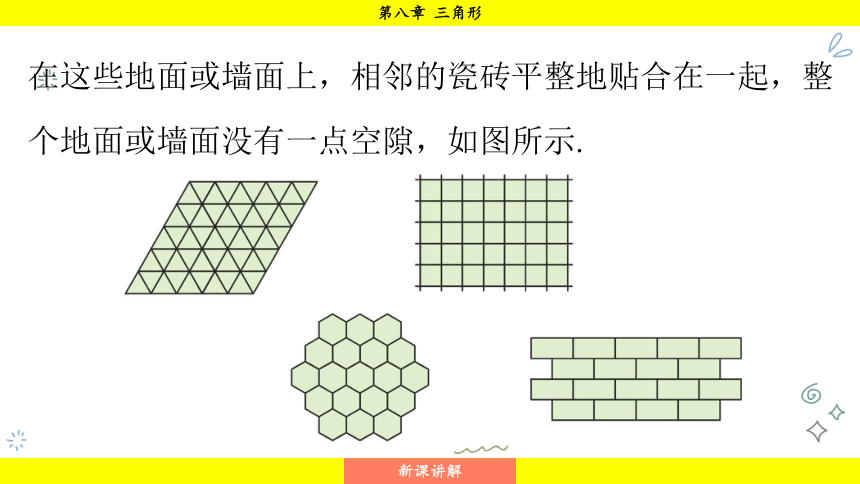
在这些地面或墙面上,相邻的瓷砖平整地贴合在一起,整个地面或墙面没有一点空隙,如图所示.
这些形状的瓷砖为什么能铺满地面而不留一点空隙呢?换一些其他形状的行不行?
为了解决这些问题,我们有必要研究多边形的有关性质.三角形是最简单的多边形,让我们从三角形开始,探究一下其中的道理.
三角形是我们早就认识的几何图形,
观察三角形的形成过程,说一说什么叫三角形
A
B
C
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形.
这三条线段就是三角形的边:线段 AB,BC,CA
三角形的概念
A
B
C
三角形的顶点采用大写字母A、B、C……表示,
如图,整个三角形记为△ABC.
如图所示,在三角形中,每两条边所组成的角叫做三角形的内角,如∠ACB;
∠A,∠B,∠C 都是三角形的内角,简称三角形的角.
不符合
不符合
不符合
辨一辨:下列图形符合三角形的定义吗?为什么?
三角形应满足以下两个条件:
① 位置关系:不在同一直线上;② 连接方式:首尾相接.
A
B
C
表示方法:
三角形用符号“△”表示,如三角形 ABC 可记作“△ABC”,读作“三角形 ABC”,
此外 △ABC 还可记作 △BCA,△CAB,△ACB 等.
基本要素:
三角形的边:边 AB、BC、CA;
三角形的顶点:顶点 A、B、C;
三角形的内角(简称为三角形的角):∠A、∠B、∠C.
特别规定:
三角形 ABC 中,顶点 A 所对的边记作 a,顶点 B 所对的边记作 b,顶点 C 所对的边记作 c .
记法:三角形 ABC 用符号表示为________.
边的表示:三角形 ABC 的边
AB、AC 和 BC 可用小写字母
分别表示为________。
△ABC
c,b,a
边 c
边 b
边 a
顶点 C
角
角
角
顶点 A
顶点 B
找一找:(1)图中有几个三角形?用符号表示出来.
(2)以 AB 为边的三角形有哪些?
A
B
C
D
E
5 个,分别是△ABE,△ABC,△BCE,△BCD,△ECD
△ABC,△ABE
找一找:(3)以 E 为顶点的三角形有哪些?
(4)以∠D 为角的三角形有哪些?
△ABE,△BCE,△CDE
△BCD,△DEC
A
B
C
D
E
找一找:(5)说出 △BCD 的三个角和三个顶点所对的边.
△BCD 的三个角是 ∠BCD、∠D 和 ∠CBD;顶点 B 所对的边为 DC,顶点 C 所对的边为 BD,顶点 D 所对的边为 BC.
A
B
C
D
E
如图,把 △ABC 的一边 BC 延长,得到∠ACD。
它与 △ABC 有何联系呢?
D
像这样,三角形的一边与另一边的延长线所组成的角,
叫做三角形的外角.
对外角∠ACD 来说,
∠ACB 是与它相邻的内角,
∠A,∠B 是与它不相邻的内角。
D
三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角,
如∠ACD是与△ABC的内角∠ACB相邻的外角.
△ABC有多少个内角?多少个外角?
与内角∠A相邻的外角有几个?它们是什么关系?
怎样画出△ABC的外角?
图中,三个三角形的内角各有什么特点?
① ② ③
三角形的分类
第一个三角形中,三个内角均为锐角;第二个三角形中,有一个内角是直角;第三个三角形中,有一个内角是钝角.
三角形可以按角来分类:
所有内角都是锐角——锐角三角形;
有一个内角是直角——直角三角形;
有一个内角是钝角——钝角三角形.
图中,三个三角形的边各有什么特点?
① ② ③
第一个三角形的三边互不相等;第二个三角形有两条边相等;第三个三角形的三边都相等.
我们把有两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;
把三条边都相等的三角形称为等边三角形(或正三角形).
等边三角形是等腰三角形吗?
按内角大小分
三角形
锐角三角形
直角三角形
钝角三角形
三角形
不等边三角形
等腰三角形
底和腰不相等的等腰三角形
等边三角形
按是否有边相等分
在图中找出等腰三角形、正三角形、锐角三角形、直角三角形和钝角三角形.
1.在练习本上画出:
(1)等腰锐角三角形;
(2)等腰直角三角形;
(3)等腰钝角三角形.
2. 6个点如图所示那样放置,相邻两点的距离相等.把这些点作为三角形的顶点,可以画多少个正三角形?
1. 三角形是指( )
A. 由三条不在同一条直线上的直线首尾顺次相接组成的平面图形
B. 由三条不在同一条直线上的线段首尾顺次连结组成的平面图形
C. 由三条线段首尾顺次连结组成的平面图形
B
2. 判断:
(1)一个钝角三角形一定不是等腰三角形。( )
(2)等边三角形是特殊的等腰三角形。( )
(3)等腰三角形的腰和底一定不相等。( )
(4)等边三角形是锐角三角形。( )
(5)直角三角形一定不是等腰三角形。( )
√
×
×
×
√
3. 如图,在 △ACE 中,∠CEA 的对边是 。
A
B
F
E
D
C
AC
定义及其 基本要素
三角形的有关概念
顶点、角、边
分类
内角
外角
分类
按角(内角大小)分类
按边(是否有边相等)分类
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
等边三角形
8.1 与三角形有关的边和角
8.1.1 认识三角形
第1课时 三角形的有关概念
一元一次不等式组的概念
↓
↓
一元一次不等式组的解集在数轴上的表示
解一元一次不等式组
一元一次不等式组
→
一元一次不等式组的解集
↓
把未知量 x 同时满足的两个一元一次不等式合在一起,就得到一元一次不等式组.
↓
利用公共部分确定不等式组的解集
在数轴上分别表示各个不等式的解集
解每个不等式
一元一次不等式组的解集在数轴上的表示
埃及金字塔
水分子结构示意图
飞机机翼
问题:
(1) 从古埃及的金字塔到现代的飞机,从宏伟的建筑
物到微小的分子结构,都有什么样的形状?
(2) 在我们的生活中有没有这样的形状呢?试举例.
瓷砖是生活中常见的装饰材料。你见过哪些形状的瓷砖?它们的形状有什么特点呢?
你知道瓷砖能铺满地面的奥秘吗?
本章将在探索与三角形有关的线段和角的基础上,研究多边形的有关性质,解开关于瓷砖铺设的一个个疑团,从中了解一些研究几何问题的基本思路和方法.
走在大街上,进入宾馆或饭店,在许多地方,我们经常可以看到由各种形状的瓷砖铺成的漂亮的地面和墙面,
在这些地面或墙面上,相邻的瓷砖平整地贴合在一起,整个地面或墙面没有一点空隙,如图所示.
这些形状的瓷砖为什么能铺满地面而不留一点空隙呢?换一些其他形状的行不行?
为了解决这些问题,我们有必要研究多边形的有关性质.三角形是最简单的多边形,让我们从三角形开始,探究一下其中的道理.
三角形是我们早就认识的几何图形,
观察三角形的形成过程,说一说什么叫三角形
A
B
C
由三条不在同一条直线上的线段首尾顺次连结组成的平面图形.
这三条线段就是三角形的边:线段 AB,BC,CA
三角形的概念
A
B
C
三角形的顶点采用大写字母A、B、C……表示,
如图,整个三角形记为△ABC.
如图所示,在三角形中,每两条边所组成的角叫做三角形的内角,如∠ACB;
∠A,∠B,∠C 都是三角形的内角,简称三角形的角.
不符合
不符合
不符合
辨一辨:下列图形符合三角形的定义吗?为什么?
三角形应满足以下两个条件:
① 位置关系:不在同一直线上;② 连接方式:首尾相接.
A
B
C
表示方法:
三角形用符号“△”表示,如三角形 ABC 可记作“△ABC”,读作“三角形 ABC”,
此外 △ABC 还可记作 △BCA,△CAB,△ACB 等.
基本要素:
三角形的边:边 AB、BC、CA;
三角形的顶点:顶点 A、B、C;
三角形的内角(简称为三角形的角):∠A、∠B、∠C.
特别规定:
三角形 ABC 中,顶点 A 所对的边记作 a,顶点 B 所对的边记作 b,顶点 C 所对的边记作 c .
记法:三角形 ABC 用符号表示为________.
边的表示:三角形 ABC 的边
AB、AC 和 BC 可用小写字母
分别表示为________。
△ABC
c,b,a
边 c
边 b
边 a
顶点 C
角
角
角
顶点 A
顶点 B
找一找:(1)图中有几个三角形?用符号表示出来.
(2)以 AB 为边的三角形有哪些?
A
B
C
D
E
5 个,分别是△ABE,△ABC,△BCE,△BCD,△ECD
△ABC,△ABE
找一找:(3)以 E 为顶点的三角形有哪些?
(4)以∠D 为角的三角形有哪些?
△ABE,△BCE,△CDE
△BCD,△DEC
A
B
C
D
E
找一找:(5)说出 △BCD 的三个角和三个顶点所对的边.
△BCD 的三个角是 ∠BCD、∠D 和 ∠CBD;顶点 B 所对的边为 DC,顶点 C 所对的边为 BD,顶点 D 所对的边为 BC.
A
B
C
D
E
如图,把 △ABC 的一边 BC 延长,得到∠ACD。
它与 △ABC 有何联系呢?
D
像这样,三角形的一边与另一边的延长线所组成的角,
叫做三角形的外角.
对外角∠ACD 来说,
∠ACB 是与它相邻的内角,
∠A,∠B 是与它不相邻的内角。
D
三角形中内角的一边与另一边的反向延长线所组成的角叫做三角形的外角,
如∠ACD是与△ABC的内角∠ACB相邻的外角.
△ABC有多少个内角?多少个外角?
与内角∠A相邻的外角有几个?它们是什么关系?
怎样画出△ABC的外角?
图中,三个三角形的内角各有什么特点?
① ② ③
三角形的分类
第一个三角形中,三个内角均为锐角;第二个三角形中,有一个内角是直角;第三个三角形中,有一个内角是钝角.
三角形可以按角来分类:
所有内角都是锐角——锐角三角形;
有一个内角是直角——直角三角形;
有一个内角是钝角——钝角三角形.
图中,三个三角形的边各有什么特点?
① ② ③
第一个三角形的三边互不相等;第二个三角形有两条边相等;第三个三角形的三边都相等.
我们把有两条边相等的三角形称为等腰三角形,相等的两边叫做等腰三角形的腰;
把三条边都相等的三角形称为等边三角形(或正三角形).
等边三角形是等腰三角形吗?
按内角大小分
三角形
锐角三角形
直角三角形
钝角三角形
三角形
不等边三角形
等腰三角形
底和腰不相等的等腰三角形
等边三角形
按是否有边相等分
在图中找出等腰三角形、正三角形、锐角三角形、直角三角形和钝角三角形.
1.在练习本上画出:
(1)等腰锐角三角形;
(2)等腰直角三角形;
(3)等腰钝角三角形.
2. 6个点如图所示那样放置,相邻两点的距离相等.把这些点作为三角形的顶点,可以画多少个正三角形?
1. 三角形是指( )
A. 由三条不在同一条直线上的直线首尾顺次相接组成的平面图形
B. 由三条不在同一条直线上的线段首尾顺次连结组成的平面图形
C. 由三条线段首尾顺次连结组成的平面图形
B
2. 判断:
(1)一个钝角三角形一定不是等腰三角形。( )
(2)等边三角形是特殊的等腰三角形。( )
(3)等腰三角形的腰和底一定不相等。( )
(4)等边三角形是锐角三角形。( )
(5)直角三角形一定不是等腰三角形。( )
√
×
×
×
√
3. 如图,在 △ACE 中,∠CEA 的对边是 。
A
B
F
E
D
C
AC
定义及其 基本要素
三角形的有关概念
顶点、角、边
分类
内角
外角
分类
按角(内角大小)分类
按边(是否有边相等)分类
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
等边三角形
