8.1.1 第2课时 三角形中的重要线段 课件(共36张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 8.1.1 第2课时 三角形中的重要线段 课件(共36张PPT)2024-2025学年数学华师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 800.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 22:18:41 | ||
图片预览




文档简介
(共36张PPT)
8.1 与三角形有关的边和角
8.1.1 认识三角形
第2课时 三角形中的重要线段
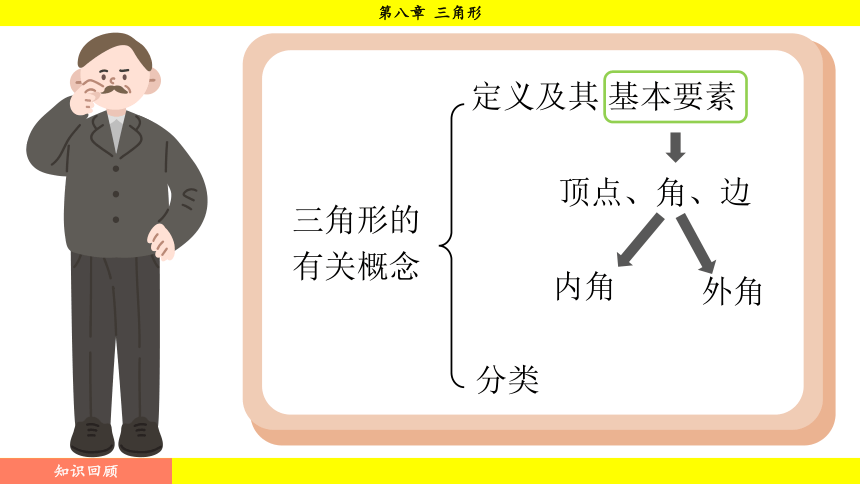
定义及其 基本要素
三角形的有关概念
顶点、角、边
分类
内角
外角
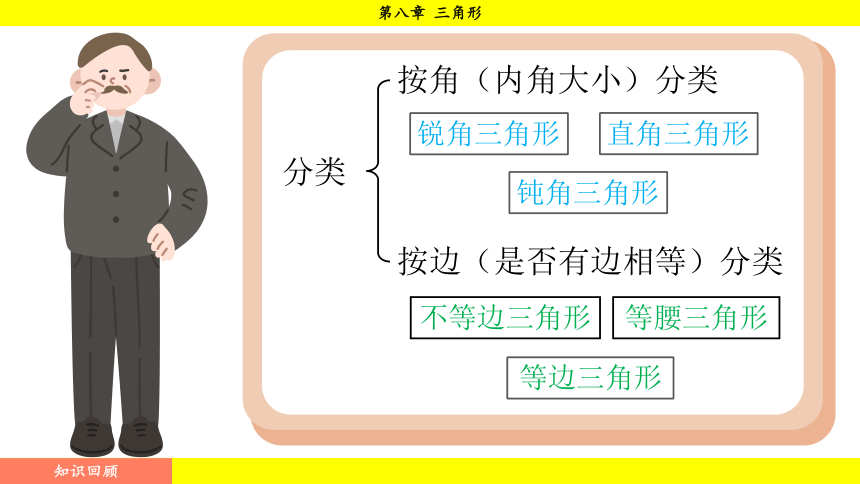
分类
按角(内角大小)分类
按边(是否有边相等)分类
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
等边三角形
1. 过直线外一点,画已知直线的垂线,能画几条,怎么画?
2. 已知 △ABC 中,BC=5cm,高 AD=4cm,求 △ABC 的面积.
只能画一条.
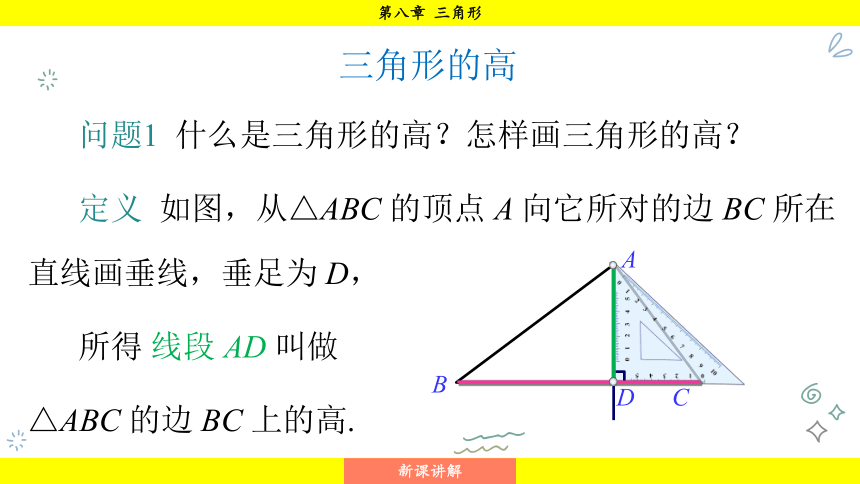
问题1 什么是三角形的高?怎样画三角形的高?
定义 如图,从△ABC 的顶点 A 向它所对的边 BC 所在直线画垂线,垂足为 D,
所得 线段 AD 叫做
△ABC 的边 BC 上的高.
A
B
C
D
三角形的高
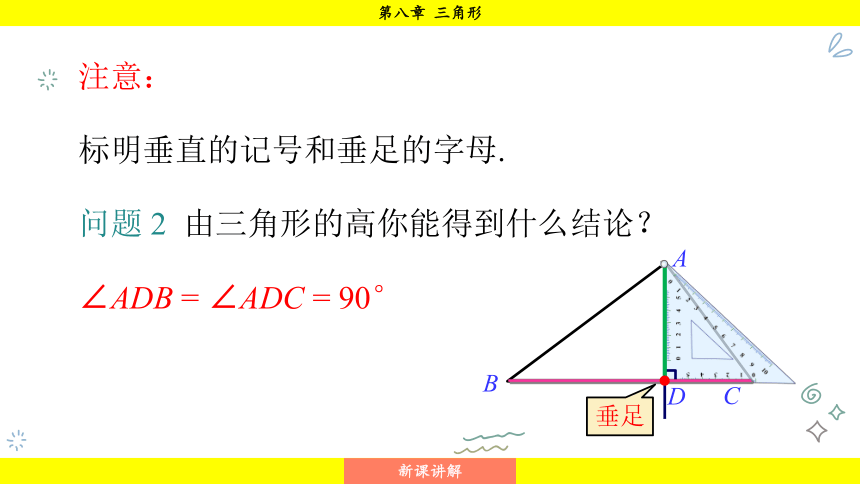
注意:
标明垂直的记号和垂足的字母.
问题 2 由三角形的高你能得到什么结论?
∠ADB = ∠ADC = 90°
A
B
C
D
垂足
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
F
O
(E,F)
O
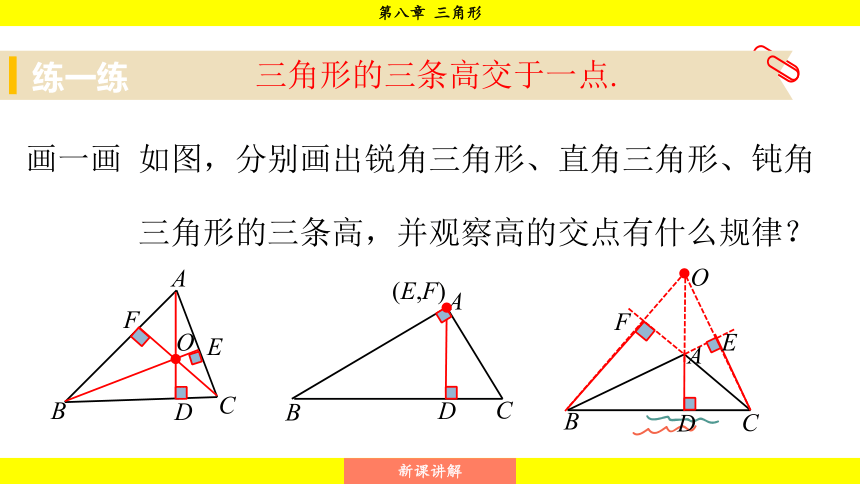
画一画 如图,分别画出锐角三角形、直角三角形、钝角
三角形的三条高,并观察高的交点有什么规律?
三角形的三条高交于一点.
画图发现
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
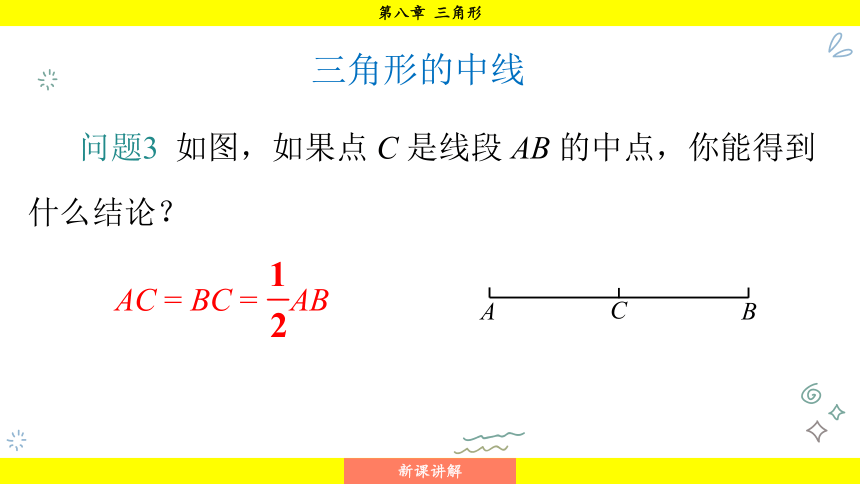
问题3 如图,如果点 C 是线段 AB 的中点,你能得到什么结论?
三角形的中线
A
C
B
AC = BC = AB
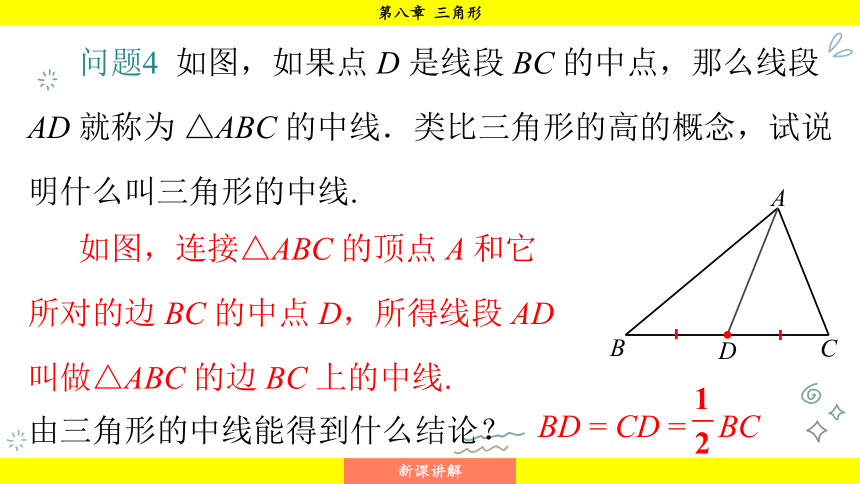
问题4 如图,如果点 D 是线段 BC 的中点,那么线段 AD 就称为 △ABC 的中线.类比三角形的高的概念,试说明什么叫三角形的中线.
如图,连接△ABC 的顶点 A 和它所对的边 BC 的中点 D,所得线段 AD 叫做△ABC 的边 BC 上的中线.
A
B
C
由三角形的中线能得到什么结论?
BD = CD = BC
D
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
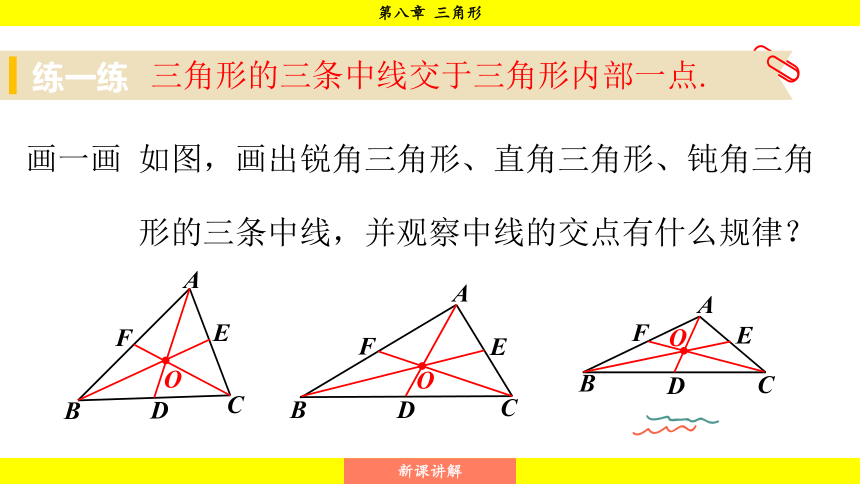
画一画 如图,画出锐角三角形、直角三角形、钝角三角
形的三条中线,并观察中线的交点有什么规律?
三角形的三条中线交于三角形内部一点.
画图发现
三角形的三条中线交于三角形内部一点,
这一点我们称为三角形的重心。
问题5 如图,在 △ABC 中,AD 是 △ABC 的中线,AE 是 △ABC 的高.试判断 △ABD 和 △ACD 的面积有什么关系,为什么?
相等,因为两个三角形等底同高,所以它们面积相等.
B
C
D
E
A
你发现了什么规律?
三角形的中线能将三角形的面积平分.
问题6 如图,若 OC 是∠AOB 的平分线,你能得到什么结论?
三角形的角平分线
A
C
B
O
∠AOC = ∠BOC
问题7 如图,在△ABC 中,如果∠BAC 的平分线 AD 交 BC 边于点 D,我们就称 AD 是 △ABC 的角平分线.类比探索三角形的高和中线的过程,你能得到哪些结论?
三角形的三条角平分线交于三角形内一点.
三角形的角平分线与角的平分线相同吗
B
C
D
A
(
(
相同点: ∠BAD = ∠CAD;
不同点:前者是线段,后者是射线.
如图所示,取△ABC边AB的中点E,连结CE,线段CE就是△ABC的一条中线;
作△ABC的内角∠BAC的平分线交
对边BC于点D,线段AD就是△ABC的
一条角平分线;
过顶点B作△ABC的边AC的垂线,垂足为点F,线段BF就是△ABC的一条高.
显然, △ABC有三条中线、
三条角平分线和三条高.
如图给出了三个相同的锐角三角形,分别在这三个三角形中画出三条中线、三条角平分线和三条高.
把锐角三角形换成直角三角形或钝角三角形,再试一试,你发现了什么?
由上面的操作,我们可以发现,三角形的三条中线、三条角平分线和三条高(或所在的直线)分别 ;直角三角形三条高的交点就是 ;钝角三角形有两条高位于三角形的外部.
交于一点
直角的顶点
题1 如图,已知 AD,AE 分别是 △ABC 的高和中线,
AB = 6cm,AC = 8cm,BC = 10cm, ∠CAB = 90 °,试求:(1) △ABE 的面积;
(2) △ACE 和 △ABE 的周长的差.
A
B
C
D
E
解:(1)
即 AD = 4.8.
A
B
C
D
E
(2) ∵AE 是 △ABC 的中线,∴BE=CE。
∴△ACE 和 △ABE 的周长的差
=(AC+AE+CE)-(AB+AE+BE)
= AC+AE+CE-AB-AE-BE = AC-AB
= 8-6 = 2(cm)
A
B
C
D
E
重要发现 三角形中线 AE 把原三角形分成的两个三角形的周长差就是 AC 与 AB 的差.
题2 如图,在△ABC 中,请画出△ABC 的∠C 的平分线;
△ABC 的边 AC 上的中线;△ABC 的边 BC 上的高.
A
B
C
D
E
F
如图,CF 是一条角平分线;BE 是 AC 边上的中线;AD 是边 BC 上的高.
1.如图,△ABC是等腰三角形,AB=AC.试画出边BC上的中线和高以及∠A的平分线.从中你发现了什么?
2.在一个直角三角形中,画出斜边上的中线,先观察一下图形中有几个等腰三角形,再用刻度尺验证你的结论.
1. 下列各组图形,哪一组图形中 AD 是△ABC 的 BC 边上的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
2. 如图,在△ABC 中,CD 是中线,
已知 BC - AC = 5 cm,△DBC 的周长为 25 cm,求△ADC 的周长.
A
D
B
C
解:∵ CD 是△ABC 的中线,
∴ BD = AD.
∵ BC - AC = 5cm,
∴△DBC 与△ADC 的周长差是 5 cm.
又∵△DBC 的周长为 25 cm,
∴△ADC 的周长为 25 - 5 = 20 (cm).
A
D
B
C
3. 如图是一张三角形纸片,请你动手画出它的BC 边上的中线,BC 边上的高,∠A 的平分线.
A
B
C
D
AD 为中线(BD=DC)
E
AE 为高(AE⊥BC)
)
)
AF 为 ∠A 的平分线(∠BAF=∠CAF)
F
4.王大爷有一块三角形菜地,现在要将它平均分给四个儿子,在菜地的一角 A 处有一口池塘,为了使分开后的四块菜地都能就近取水,
你能帮帮王大爷吗 如果不考虑水源,
还可以怎样分
A
思路提示:
想到三角形的中线能把三角形分成面积相等的两部分.
A
三角形中的重要线段
高
钝角三角形两短边上的高的画法
中线
角平分线
是线段,不是射线
中线
会把原三角形的面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
8.1 与三角形有关的边和角
8.1.1 认识三角形
第2课时 三角形中的重要线段
定义及其 基本要素
三角形的有关概念
顶点、角、边
分类
内角
外角
分类
按角(内角大小)分类
按边(是否有边相等)分类
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
等边三角形
1. 过直线外一点,画已知直线的垂线,能画几条,怎么画?
2. 已知 △ABC 中,BC=5cm,高 AD=4cm,求 △ABC 的面积.
只能画一条.
问题1 什么是三角形的高?怎样画三角形的高?
定义 如图,从△ABC 的顶点 A 向它所对的边 BC 所在直线画垂线,垂足为 D,
所得 线段 AD 叫做
△ABC 的边 BC 上的高.
A
B
C
D
三角形的高
注意:
标明垂直的记号和垂足的字母.
问题 2 由三角形的高你能得到什么结论?
∠ADB = ∠ADC = 90°
A
B
C
D
垂足
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
F
O
(E,F)
O
画一画 如图,分别画出锐角三角形、直角三角形、钝角
三角形的三条高,并观察高的交点有什么规律?
三角形的三条高交于一点.
画图发现
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
问题3 如图,如果点 C 是线段 AB 的中点,你能得到什么结论?
三角形的中线
A
C
B
AC = BC = AB
问题4 如图,如果点 D 是线段 BC 的中点,那么线段 AD 就称为 △ABC 的中线.类比三角形的高的概念,试说明什么叫三角形的中线.
如图,连接△ABC 的顶点 A 和它所对的边 BC 的中点 D,所得线段 AD 叫做△ABC 的边 BC 上的中线.
A
B
C
由三角形的中线能得到什么结论?
BD = CD = BC
D
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
画一画 如图,画出锐角三角形、直角三角形、钝角三角
形的三条中线,并观察中线的交点有什么规律?
三角形的三条中线交于三角形内部一点.
画图发现
三角形的三条中线交于三角形内部一点,
这一点我们称为三角形的重心。
问题5 如图,在 △ABC 中,AD 是 △ABC 的中线,AE 是 △ABC 的高.试判断 △ABD 和 △ACD 的面积有什么关系,为什么?
相等,因为两个三角形等底同高,所以它们面积相等.
B
C
D
E
A
你发现了什么规律?
三角形的中线能将三角形的面积平分.
问题6 如图,若 OC 是∠AOB 的平分线,你能得到什么结论?
三角形的角平分线
A
C
B
O
∠AOC = ∠BOC
问题7 如图,在△ABC 中,如果∠BAC 的平分线 AD 交 BC 边于点 D,我们就称 AD 是 △ABC 的角平分线.类比探索三角形的高和中线的过程,你能得到哪些结论?
三角形的三条角平分线交于三角形内一点.
三角形的角平分线与角的平分线相同吗
B
C
D
A
(
(
相同点: ∠BAD = ∠CAD;
不同点:前者是线段,后者是射线.
如图所示,取△ABC边AB的中点E,连结CE,线段CE就是△ABC的一条中线;
作△ABC的内角∠BAC的平分线交
对边BC于点D,线段AD就是△ABC的
一条角平分线;
过顶点B作△ABC的边AC的垂线,垂足为点F,线段BF就是△ABC的一条高.
显然, △ABC有三条中线、
三条角平分线和三条高.
如图给出了三个相同的锐角三角形,分别在这三个三角形中画出三条中线、三条角平分线和三条高.
把锐角三角形换成直角三角形或钝角三角形,再试一试,你发现了什么?
由上面的操作,我们可以发现,三角形的三条中线、三条角平分线和三条高(或所在的直线)分别 ;直角三角形三条高的交点就是 ;钝角三角形有两条高位于三角形的外部.
交于一点
直角的顶点
题1 如图,已知 AD,AE 分别是 △ABC 的高和中线,
AB = 6cm,AC = 8cm,BC = 10cm, ∠CAB = 90 °,试求:(1) △ABE 的面积;
(2) △ACE 和 △ABE 的周长的差.
A
B
C
D
E
解:(1)
即 AD = 4.8.
A
B
C
D
E
(2) ∵AE 是 △ABC 的中线,∴BE=CE。
∴△ACE 和 △ABE 的周长的差
=(AC+AE+CE)-(AB+AE+BE)
= AC+AE+CE-AB-AE-BE = AC-AB
= 8-6 = 2(cm)
A
B
C
D
E
重要发现 三角形中线 AE 把原三角形分成的两个三角形的周长差就是 AC 与 AB 的差.
题2 如图,在△ABC 中,请画出△ABC 的∠C 的平分线;
△ABC 的边 AC 上的中线;△ABC 的边 BC 上的高.
A
B
C
D
E
F
如图,CF 是一条角平分线;BE 是 AC 边上的中线;AD 是边 BC 上的高.
1.如图,△ABC是等腰三角形,AB=AC.试画出边BC上的中线和高以及∠A的平分线.从中你发现了什么?
2.在一个直角三角形中,画出斜边上的中线,先观察一下图形中有几个等腰三角形,再用刻度尺验证你的结论.
1. 下列各组图形,哪一组图形中 AD 是△ABC 的 BC 边上的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
D
2. 如图,在△ABC 中,CD 是中线,
已知 BC - AC = 5 cm,△DBC 的周长为 25 cm,求△ADC 的周长.
A
D
B
C
解:∵ CD 是△ABC 的中线,
∴ BD = AD.
∵ BC - AC = 5cm,
∴△DBC 与△ADC 的周长差是 5 cm.
又∵△DBC 的周长为 25 cm,
∴△ADC 的周长为 25 - 5 = 20 (cm).
A
D
B
C
3. 如图是一张三角形纸片,请你动手画出它的BC 边上的中线,BC 边上的高,∠A 的平分线.
A
B
C
D
AD 为中线(BD=DC)
E
AE 为高(AE⊥BC)
)
)
AF 为 ∠A 的平分线(∠BAF=∠CAF)
F
4.王大爷有一块三角形菜地,现在要将它平均分给四个儿子,在菜地的一角 A 处有一口池塘,为了使分开后的四块菜地都能就近取水,
你能帮帮王大爷吗 如果不考虑水源,
还可以怎样分
A
思路提示:
想到三角形的中线能把三角形分成面积相等的两部分.
A
三角形中的重要线段
高
钝角三角形两短边上的高的画法
中线
角平分线
是线段,不是射线
中线
会把原三角形的面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
