8.1.3 三角形的三边关系 课件(共33张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 8.1.3 三角形的三边关系 课件(共33张PPT)2024-2025学年数学华师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 22:19:01 | ||
图片预览





文档简介
(共33张PPT)
8.1 与三角形有关的边和角
8.1.3 三角形的三边关系
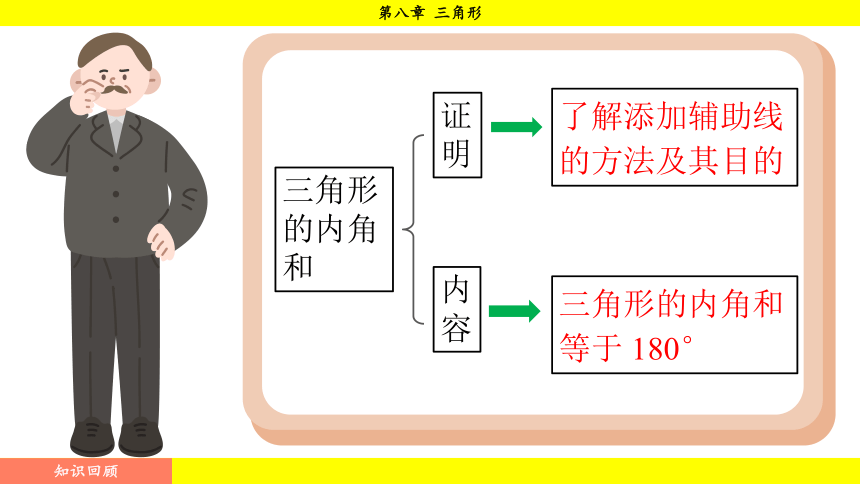
三角形的内角和
证明
了解添加辅助线的方法及其目的
内容
三角形的内角和等于 180°
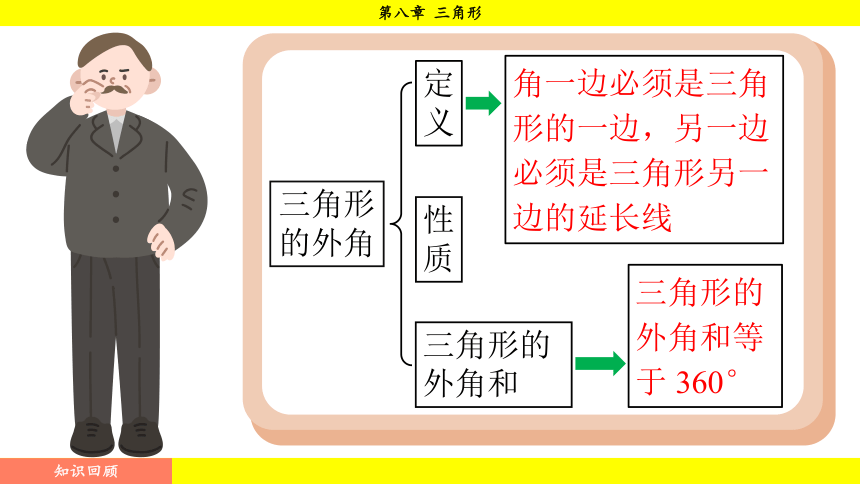
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的外角和
三角形的外角和等于 360°
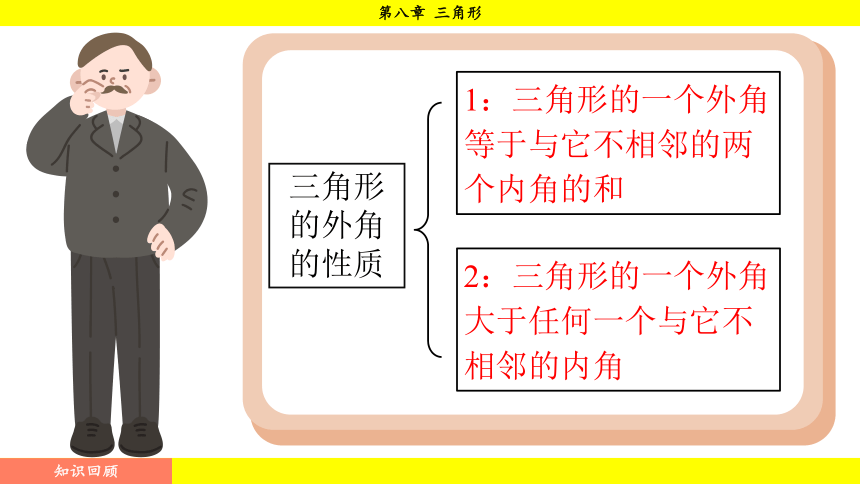
三角形的外角的性质
1:三角形的一个外角等于与它不相邻的两个内角的和
2:三角形的一个外角大于任何一个与它不相邻的内角
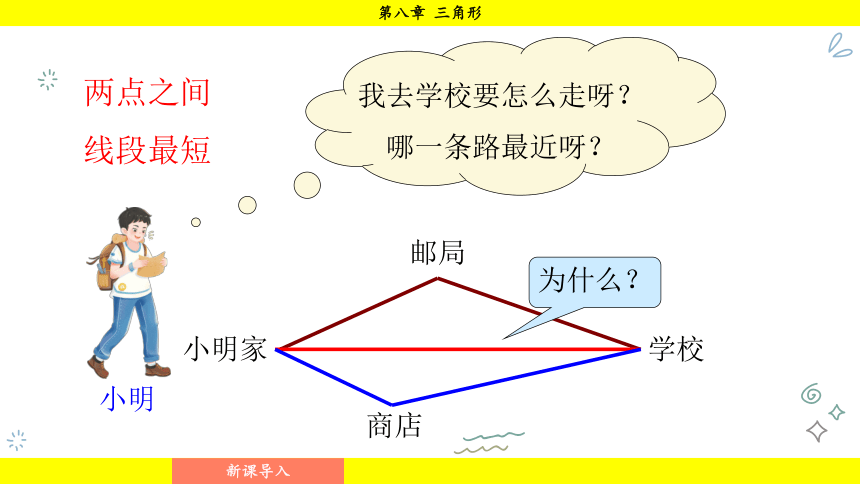
我去学校要怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
商店
小明家
小明
两点之间线段最短
在小学阶段,我们已经通过观察或度量,了解到“三角形的任意两边之和大于第三边”这样一个事实,现在让我们通过作三角形的过程,再次体会这一结论.
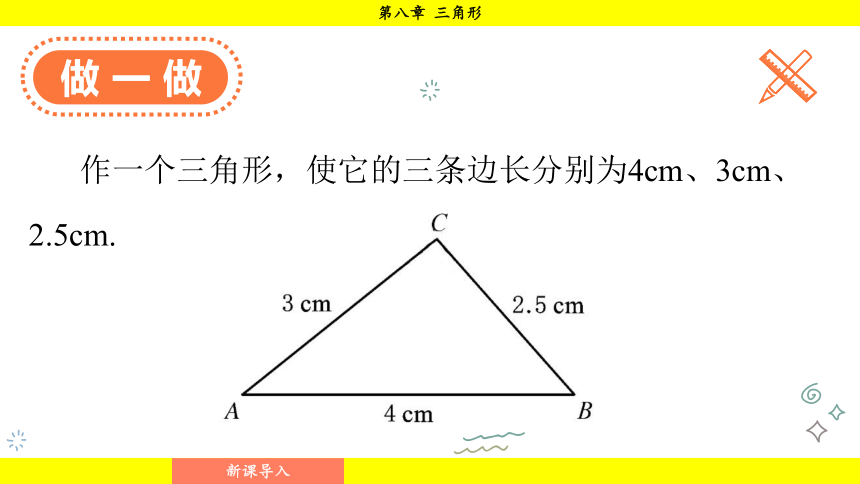
作一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
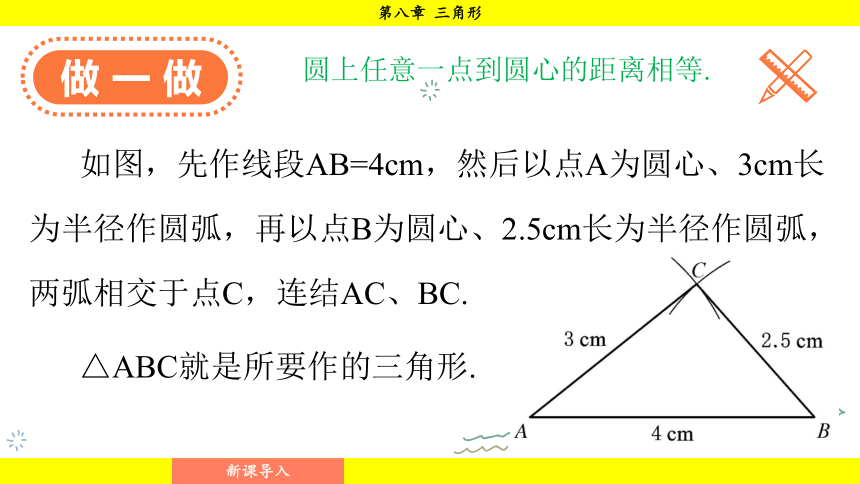
如图,先作线段AB=4cm,然后以点A为圆心、3cm长为半径作圆弧,再以点B为圆心、2.5cm长为半径作圆弧,两弧相交于点C,连结AC、BC.
△ABC就是所要作的三角形.
圆上任意一点到圆心的距离相等.
现有12条已知长度的线段:三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.任意选择三条线段作三角形,使它的三条边长分别为你所选择的三条线段的长.
说说你的发现与想法.
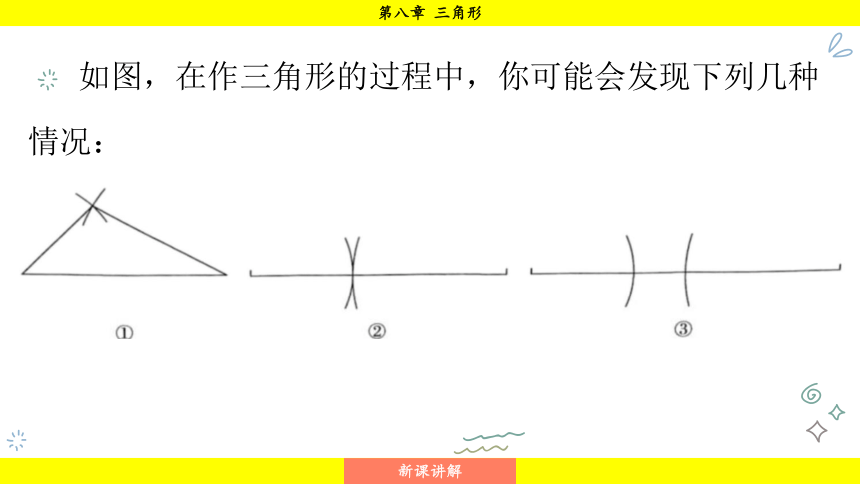
如图,在作三角形的过程中,你可能会发现下列几种情况:
因此,并不是任意三条线段都可以组成一个三角形.
在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形.
换句话说:
三角形的任意两边之和大于第三边.
三角形的三边关系定理
AC+BC>AB
AC>AB-BC
AB+BC>AC
BC>AC-AB
AC+AB>BC
AB>BC-AC
A
B
C
想一想:由不等式的变形,三角形的两边之差
与第三边有何关系?
三角形任何两边的差小于第三边.
三角形的三边关系定理的理论根据是?
两点之间,线段最短.
等腰三角形中,周长为 18 cm.
(1) 如果腰长是底边长的 2 倍,求各边长;
(2) 如果一边长为 4 cm,求另两边长。
解:(1) 设底边长为 x cm,则腰长为 2x cm,
x + 2x + 2x = 18.
解得 x = 3.6.
所以三边长分别为 3.6 cm、7.2 cm、7.2 cm.
(2) 因为长为 4 cm 的边可能是腰,也可能是底边,
所以需要分情况讨论.
① 若底边长为 4 cm,设腰长为 x cm,则有
4 + 2x = 18. 解得 x = 7.
② 若腰长为 4 cm,设底边长为 x cm,则有
2×4 + x = 18. 解得 x = 10.
因为 4 + 4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长是 4 cm 的等腰三角形.
所以,三角形的另两边长都是 7 cm.
用三根木条钉一个三角形,你会发现再也无法改变这个三角形的形状和大小,
也就是说,如果三角形的三条边固定,那么三角形的形状和大小就完全确定了.
三角形的这个性质叫做三角形的稳定性.
理解“稳定性”
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.这就是说,三角形的稳定性不是“拉得动或拉不动”的问题,其实质应是“三角形的边长一旦确定,其形状和大小就确定了”.
用四根木条钉一个四边形,你会发现这个四边形的形状和大小都可以改变,
这说明四边形不具有稳定性.
问题:如图,盖房子时,在木框未安装好之前,木工师傅常常先在木框上斜钉一根木条,为什么要这样做呢?
三角形形状不会改变,四边形形状会改变,这就是说,三角形具有稳定性,四边形不具有稳定性。
三角形的稳定性在生产实践中有着广泛的应用.如图是位于中国新疆维吾尔自治
区境内的果子沟大桥,它是
新疆重要民生工程,其拉索
就是三角形结构.
1.(口答)下列长度的各组线段能否组成一个三角形?
(1)15cm,10cm,7cm;
(2)4cm,5cm,10cm;
(3)3cm,8cm,5cm;
(4)4cm,5cm,6cm.
2.一木工有两根长分别为40cm和60cm的木条,要另找一根木条,钉成一个三角木架.问:第三根木条的长度应在什么范围内?
3.举两个三角形的稳定性在实际生活中应用的例子.
1. 下列长度的三条线段能否组成三角形?为什么?
(1)3,4,8 ( )
(2)2,5,6 ( )
(3)5,6,10 ( )
(4)3,5,8 ( )
不能
能
能
不能
2. 五条线段的长分别为 1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成__个三角形.
3. 如果等腰三角形的一边长是 5 cm,另一边长是 8 cm,则这个等腰三角形的周长为__________cm.
3
18 或 21
4. 如果等腰三角形的一边长是 4 cm,另一边长是 9 cm,则这个等腰三角形的周长为______cm.
5. 小颖要制作一个三角形木架,现有两根长度为 8cm和 5cm 的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
22
解:设第三根木棒长为 x cm,有
8-5<x<8+5
3<x<13
∵x 为偶数, ∴小颖有 5 种选法.
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm.
6.要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形以保持形状,那么要使五边形、六边形、七边形木架保持稳定该怎么办呢
三角形的三边关系
三角形的三边关系:任何两边之和大于第三边,任何两边之差小于第三边
应用
稳定性
三角形
独有性质
应用
8.1 与三角形有关的边和角
8.1.3 三角形的三边关系
三角形的内角和
证明
了解添加辅助线的方法及其目的
内容
三角形的内角和等于 180°
三角形的外角
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的外角和
三角形的外角和等于 360°
三角形的外角的性质
1:三角形的一个外角等于与它不相邻的两个内角的和
2:三角形的一个外角大于任何一个与它不相邻的内角
我去学校要怎么走呀?哪一条路最近呀?
为什么?
邮局
学校
商店
小明家
小明
两点之间线段最短
在小学阶段,我们已经通过观察或度量,了解到“三角形的任意两边之和大于第三边”这样一个事实,现在让我们通过作三角形的过程,再次体会这一结论.
作一个三角形,使它的三条边长分别为4cm、3cm、2.5cm.
如图,先作线段AB=4cm,然后以点A为圆心、3cm长为半径作圆弧,再以点B为圆心、2.5cm长为半径作圆弧,两弧相交于点C,连结AC、BC.
△ABC就是所要作的三角形.
圆上任意一点到圆心的距离相等.
现有12条已知长度的线段:三条长2cm、三条长3cm、两条长4cm、两条长5cm、两条长6cm.任意选择三条线段作三角形,使它的三条边长分别为你所选择的三条线段的长.
说说你的发现与想法.
如图,在作三角形的过程中,你可能会发现下列几种情况:
因此,并不是任意三条线段都可以组成一个三角形.
在三条线段中,如果两条较短线段的和不大于第三条线段,那么这三条线段就不能组成一个三角形.
换句话说:
三角形的任意两边之和大于第三边.
三角形的三边关系定理
AC+BC>AB
AC>AB-BC
AB+BC>AC
BC>AC-AB
AC+AB>BC
AB>BC-AC
A
B
C
想一想:由不等式的变形,三角形的两边之差
与第三边有何关系?
三角形任何两边的差小于第三边.
三角形的三边关系定理的理论根据是?
两点之间,线段最短.
等腰三角形中,周长为 18 cm.
(1) 如果腰长是底边长的 2 倍,求各边长;
(2) 如果一边长为 4 cm,求另两边长。
解:(1) 设底边长为 x cm,则腰长为 2x cm,
x + 2x + 2x = 18.
解得 x = 3.6.
所以三边长分别为 3.6 cm、7.2 cm、7.2 cm.
(2) 因为长为 4 cm 的边可能是腰,也可能是底边,
所以需要分情况讨论.
① 若底边长为 4 cm,设腰长为 x cm,则有
4 + 2x = 18. 解得 x = 7.
② 若腰长为 4 cm,设底边长为 x cm,则有
2×4 + x = 18. 解得 x = 10.
因为 4 + 4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长是 4 cm 的等腰三角形.
所以,三角形的另两边长都是 7 cm.
用三根木条钉一个三角形,你会发现再也无法改变这个三角形的形状和大小,
也就是说,如果三角形的三条边固定,那么三角形的形状和大小就完全确定了.
三角形的这个性质叫做三角形的稳定性.
理解“稳定性”
只要三角形三条边的长度固定,这个三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.这就是说,三角形的稳定性不是“拉得动或拉不动”的问题,其实质应是“三角形的边长一旦确定,其形状和大小就确定了”.
用四根木条钉一个四边形,你会发现这个四边形的形状和大小都可以改变,
这说明四边形不具有稳定性.
问题:如图,盖房子时,在木框未安装好之前,木工师傅常常先在木框上斜钉一根木条,为什么要这样做呢?
三角形形状不会改变,四边形形状会改变,这就是说,三角形具有稳定性,四边形不具有稳定性。
三角形的稳定性在生产实践中有着广泛的应用.如图是位于中国新疆维吾尔自治
区境内的果子沟大桥,它是
新疆重要民生工程,其拉索
就是三角形结构.
1.(口答)下列长度的各组线段能否组成一个三角形?
(1)15cm,10cm,7cm;
(2)4cm,5cm,10cm;
(3)3cm,8cm,5cm;
(4)4cm,5cm,6cm.
2.一木工有两根长分别为40cm和60cm的木条,要另找一根木条,钉成一个三角木架.问:第三根木条的长度应在什么范围内?
3.举两个三角形的稳定性在实际生活中应用的例子.
1. 下列长度的三条线段能否组成三角形?为什么?
(1)3,4,8 ( )
(2)2,5,6 ( )
(3)5,6,10 ( )
(4)3,5,8 ( )
不能
能
能
不能
2. 五条线段的长分别为 1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成__个三角形.
3. 如果等腰三角形的一边长是 5 cm,另一边长是 8 cm,则这个等腰三角形的周长为__________cm.
3
18 或 21
4. 如果等腰三角形的一边长是 4 cm,另一边长是 9 cm,则这个等腰三角形的周长为______cm.
5. 小颖要制作一个三角形木架,现有两根长度为 8cm和 5cm 的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
22
解:设第三根木棒长为 x cm,有
8-5<x<8+5
3<x<13
∵x 为偶数, ∴小颖有 5 种选法.
第三根木棒的长度可以是:4cm,6cm,8cm,10cm,12cm.
6.要使四边形木架不变形,至少要钉上一根木条,把它分成两个三角形以保持形状,那么要使五边形、六边形、七边形木架保持稳定该怎么办呢
三角形的三边关系
三角形的三边关系:任何两边之和大于第三边,任何两边之差小于第三边
应用
稳定性
三角形
独有性质
应用
