8.2.1 多边形的内角和 课件(共33张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 8.2.1 多边形的内角和 课件(共33张PPT)2024-2025学年数学华师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 00:00:00 | ||
图片预览





文档简介
(共33张PPT)
8.2 多边形的内角和与外角和
8.2.1 多边形的内角和
三角形的三边关系
三角形的三边关系:任何两边之和大于第三边,任何两边之差小于第三边
应用
稳定性
三角形
独有性质
应用
生活中的平面图形
三角形
六边形
长方形
四边形
八边形
三角形有三个内角、三条边,我们也可以把三角形称为三边形.
我们已经知道什么叫做三角形,即三边形.
你能说出什么叫做四边形、五边形吗?
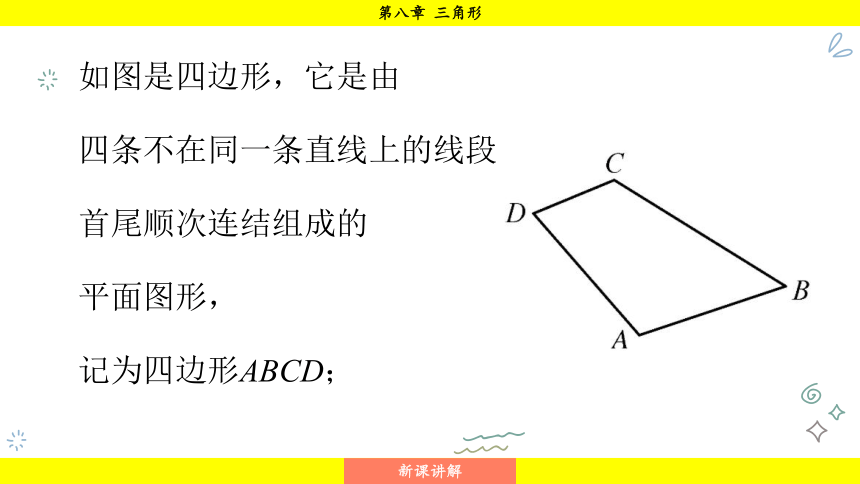
如图是四边形,它是由
四条不在同一条直线上的线段
首尾顺次连结组成的
平面图形,
记为四边形ABCD;
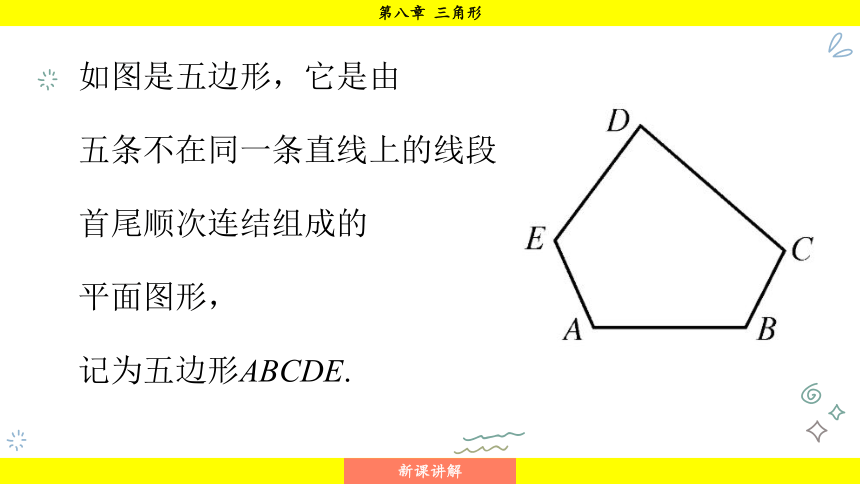
如图是五边形,它是由
五条不在同一条直线上的线段
首尾顺次连结组成的
平面图形,
记为五边形ABCDE.
一般地,由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形.
注意 我们现在研究的是如上图所示的多边形,也就是凸多边形.
如果把多边形的任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
如图 1 是凸多边形; 图 2 不是凸多边形.
今后如果不作说明,我们讲的多边形都是凸多边形.
图 2
图 1
A
C
B
D
A
C
B
D
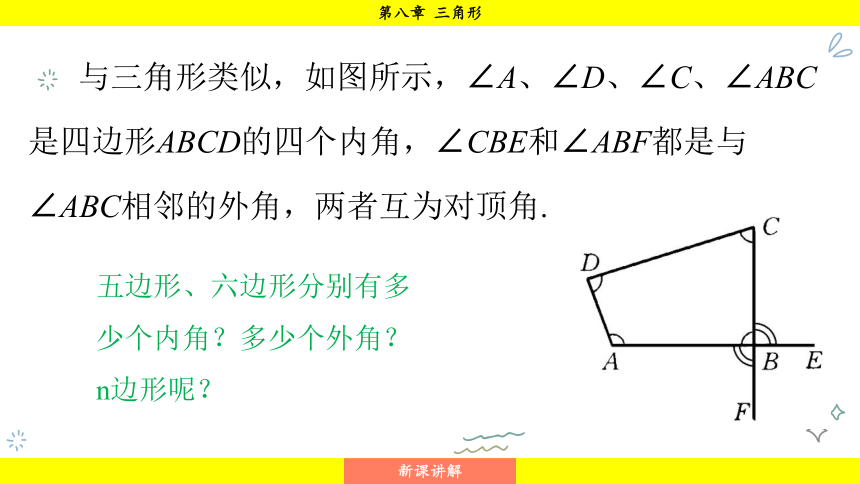
与三角形类似,如图所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角,∠CBE和∠ABF都是与∠ABC相邻的外角,两者互为对顶角.
五边形、六边形分别有多少个内角?多少个外角?n边形呢?
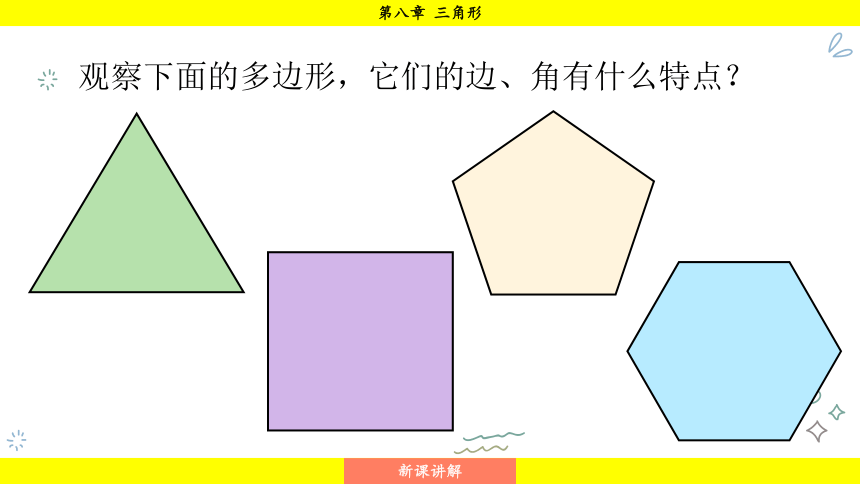
观察下面的多边形,它们的边、角有什么特点?
一般地,如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
如正三角形、
正四边形(正方形)、
正五边形等.
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.例如,图①中,线段AC是四边形ABCD的一条对角线;图②③中,虚线表示的线段也是所画多边形的对角线.
① ② ③
顶点
内角
边
对角线
(连结不相邻两个顶点的线段)
多边形的相关元素
外角
表示:五边形ABCDE
A
C
B
D
E
由上图可以看出,从多边形的一个顶点引出的对角线把多边形划分为若干个三角形.我们已知一个三角形的内角和等于180°,那么四边形的内角和等于多少呢?五边形、六边形呢?一般地,n边形的内角和等于多少呢?
为了求得n边形的内角和,请根据下图,完成表格.
以下面的四边形为例:
如图,一条对角线把四边形分成两个三角形,
可以看出,四边形的内角和
等于这两个三角形的内角和,
即 180°×2=360°.
由此,我们得出
n边形的内角和为(n-2)·180°.
3
4
5
n-2
3×180°
4×180°
5×180°
(n-2)
×180°
“归纳推理”是数学中的一种推理方式,体现了从特殊到一般的推理过程.在这里,我们通过对三边形、四边形、五边形等的探索,发现它们的内角和与边数之间存在某种逻辑关系,从而归纳出多边形的内角和公式.
这种归纳推理的方式,我们今后还会经常用到.当然,“看”出来的数学结论未必一定正确,但它们还是给我们指引了研究的方向.因此,归纳推理和演绎推理相结合是必要的.
例1 求八边形的内角和.
解: 八边形的内角和为
=(8-2)×180°
(n-2)·180°
=1080°.
例2 已知一个多边形的内角和等于 2160°,求这个多边形的边数.
解: 设这个多边形的边数为 n,根据题意,得
(n-2 )·180°= 2160°.
解得 n = 14.
因此,这个多边形的边数为14.
如图,在n边形(图中取n=6的情形)内任取一点P,连结点P与多边形的每一个顶点,可得到几个三角形?你能否根据这样划分多边形的方法来说
明n边形的内角和等于(n-2)·180°?
为了说明多边形的内角和公式,我们已经尝试用两种方法划分多边形.这里是在多边形内任取一点,前面可以看作是任取一个顶点.那么是否还可以
移动点P,引出其他方法呢?
试试看,你一定会有新的发现.
1.求下列图形中x的值.
(1) (2)
2.已知一个多边形的内角和等于1440°,求这个多边形的边数.
1. 判断.
(1) 当多边形边数增加时,它的内角和也随着增加. ( )
(2) 从 n 边形一个顶点出发,可以引出 (n-2) 条对角线,得到(n-2) 个三角形. ( )
2. 五边形的内角和为 ,它的对角线有 条。
3. 如果一个多边形的边数增加一条,那么这个多边形的内角和增加______,外角和增加_____.
540°
5
180°
0°
4. 一个多边形的内角和不可能是 ( )
A. 1800° B. 540 ° C. 720 ° D. 810 °
5. 一个多边形从一个顶点可引对角线 3 条,这个多边形内角和等于 ( )
A. 360° B. 540 ° C. 720 ° D. 900 °
D
C
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥ 3 的整数)
多边形的定义
由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形
8.2 多边形的内角和与外角和
8.2.1 多边形的内角和
三角形的三边关系
三角形的三边关系:任何两边之和大于第三边,任何两边之差小于第三边
应用
稳定性
三角形
独有性质
应用
生活中的平面图形
三角形
六边形
长方形
四边形
八边形
三角形有三个内角、三条边,我们也可以把三角形称为三边形.
我们已经知道什么叫做三角形,即三边形.
你能说出什么叫做四边形、五边形吗?
如图是四边形,它是由
四条不在同一条直线上的线段
首尾顺次连结组成的
平面图形,
记为四边形ABCD;
如图是五边形,它是由
五条不在同一条直线上的线段
首尾顺次连结组成的
平面图形,
记为五边形ABCDE.
一般地,由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形.
注意 我们现在研究的是如上图所示的多边形,也就是凸多边形.
如果把多边形的任何一边双向延长,其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形.
如图 1 是凸多边形; 图 2 不是凸多边形.
今后如果不作说明,我们讲的多边形都是凸多边形.
图 2
图 1
A
C
B
D
A
C
B
D
与三角形类似,如图所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角,∠CBE和∠ABF都是与∠ABC相邻的外角,两者互为对顶角.
五边形、六边形分别有多少个内角?多少个外角?n边形呢?
观察下面的多边形,它们的边、角有什么特点?
一般地,如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形.
如正三角形、
正四边形(正方形)、
正五边形等.
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.例如,图①中,线段AC是四边形ABCD的一条对角线;图②③中,虚线表示的线段也是所画多边形的对角线.
① ② ③
顶点
内角
边
对角线
(连结不相邻两个顶点的线段)
多边形的相关元素
外角
表示:五边形ABCDE
A
C
B
D
E
由上图可以看出,从多边形的一个顶点引出的对角线把多边形划分为若干个三角形.我们已知一个三角形的内角和等于180°,那么四边形的内角和等于多少呢?五边形、六边形呢?一般地,n边形的内角和等于多少呢?
为了求得n边形的内角和,请根据下图,完成表格.
以下面的四边形为例:
如图,一条对角线把四边形分成两个三角形,
可以看出,四边形的内角和
等于这两个三角形的内角和,
即 180°×2=360°.
由此,我们得出
n边形的内角和为(n-2)·180°.
3
4
5
n-2
3×180°
4×180°
5×180°
(n-2)
×180°
“归纳推理”是数学中的一种推理方式,体现了从特殊到一般的推理过程.在这里,我们通过对三边形、四边形、五边形等的探索,发现它们的内角和与边数之间存在某种逻辑关系,从而归纳出多边形的内角和公式.
这种归纳推理的方式,我们今后还会经常用到.当然,“看”出来的数学结论未必一定正确,但它们还是给我们指引了研究的方向.因此,归纳推理和演绎推理相结合是必要的.
例1 求八边形的内角和.
解: 八边形的内角和为
=(8-2)×180°
(n-2)·180°
=1080°.
例2 已知一个多边形的内角和等于 2160°,求这个多边形的边数.
解: 设这个多边形的边数为 n,根据题意,得
(n-2 )·180°= 2160°.
解得 n = 14.
因此,这个多边形的边数为14.
如图,在n边形(图中取n=6的情形)内任取一点P,连结点P与多边形的每一个顶点,可得到几个三角形?你能否根据这样划分多边形的方法来说
明n边形的内角和等于(n-2)·180°?
为了说明多边形的内角和公式,我们已经尝试用两种方法划分多边形.这里是在多边形内任取一点,前面可以看作是任取一个顶点.那么是否还可以
移动点P,引出其他方法呢?
试试看,你一定会有新的发现.
1.求下列图形中x的值.
(1) (2)
2.已知一个多边形的内角和等于1440°,求这个多边形的边数.
1. 判断.
(1) 当多边形边数增加时,它的内角和也随着增加. ( )
(2) 从 n 边形一个顶点出发,可以引出 (n-2) 条对角线,得到(n-2) 个三角形. ( )
2. 五边形的内角和为 ,它的对角线有 条。
3. 如果一个多边形的边数增加一条,那么这个多边形的内角和增加______,外角和增加_____.
540°
5
180°
0°
4. 一个多边形的内角和不可能是 ( )
A. 1800° B. 540 ° C. 720 ° D. 810 °
5. 一个多边形从一个顶点可引对角线 3 条,这个多边形内角和等于 ( )
A. 360° B. 540 ° C. 720 ° D. 900 °
D
C
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥ 3 的整数)
多边形的定义
由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形
