8.2.2 多边形的外角和 课件(共25张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 8.2.2 多边形的外角和 课件(共25张PPT)2024-2025学年数学华师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 957.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
8.2 多边形的内角和与外角和
8.2.2 多边形的外角和
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥ 3 的整数)
多边形的定义
由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形
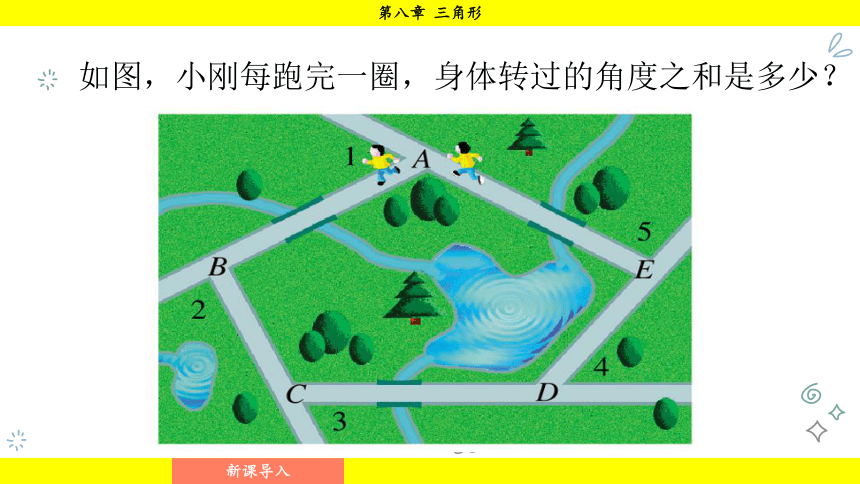
如图,小刚每跑完一圈,身体转过的角度之和是多少?
与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角.
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
如图,∠1+∠2+∠3+∠4就是四边形ABCD的外角和.
从图中可以知道:
(∠1+∠5)+(∠2+∠6)+
(∠3+∠7)+(∠4+∠8) =4×180°,
所以 ∠1+∠2+∠3+∠4 = 4 × 180°-(∠5+∠6+∠7+∠8).
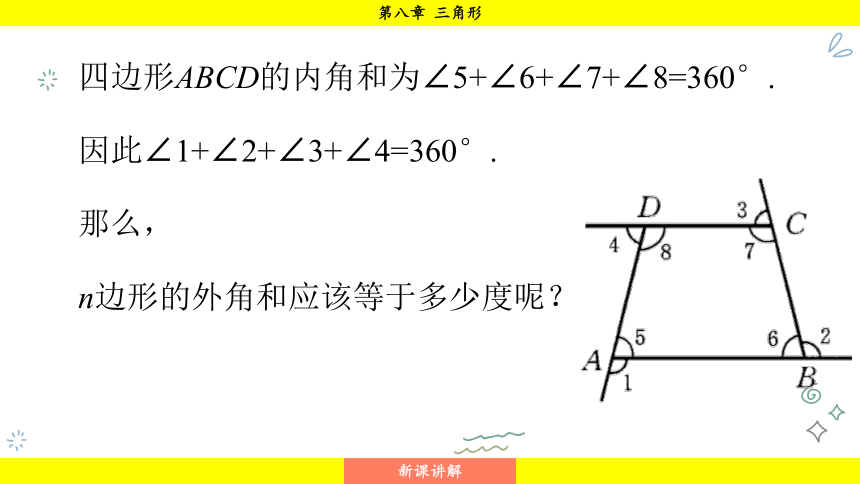
四边形ABCD的内角和为∠5+∠6+∠7+∠8=360°.
因此∠1+∠2+∠3+∠4=360°.
那么,
n边形的外角和应该等于多少度呢?
如图,从与每个内角相邻的两个外角中分别取一个:
1. 任意一个外角与和它相邻
的内角有什么关系?
2. 五个外角加上它们相邻的
五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
5×180°= 900°
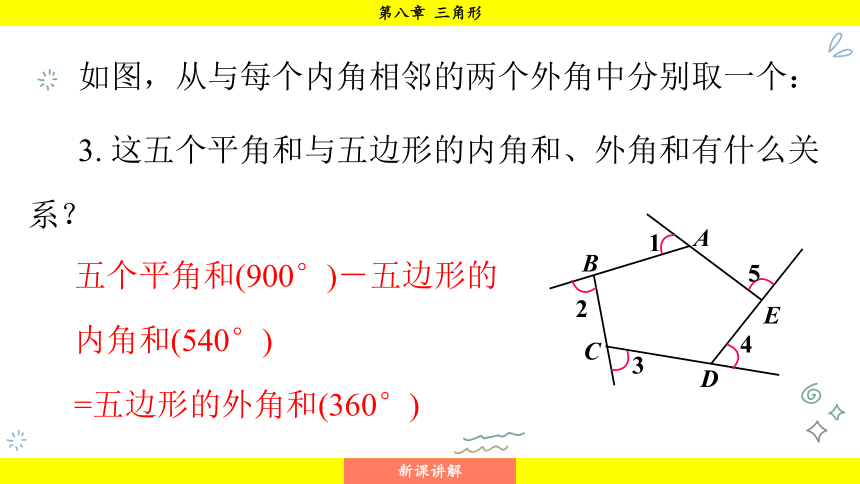
如图,从与每个内角相邻的两个外角中分别取一个:
3. 这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
五个平角和(900°)-五边形的内角和(540°)
=五边形的外角和(360°)
根据n边形的每一个内角与和它相邻的外角都互为补角,可以求得n边形的外角和.据此,请将数据填入表中.
360°
360°
360°
360°
360°
4×
180°
= 720°
5×
180°
= 900°
6×
180°
= 1080°
7×
180°
= 1260°
n×
180°
360°
540°
720°
900°
(n-2)
×180°
因此,任意多边形的外角和都为360°.
与 n 边形的每个内角相邻的外角分别有两个, 这两个外角是对顶角.
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为 n 边形的外角和.
n 边形外角和
-(n-2) × 180°
=360 °
= n 个平角和-n 边形内角和
= n×180 °
即,n边形的外角和等于360度.
例3 一个多边形的每个外角都是72°,这个多边形是几边形?
解: 设这个多边形的边数为 n,根据题意,得
n·72°=360°.
解得 n = 5.
因此,这个多边形是五边形.
例4 一个多边形的内角和等于它外角和的 5 倍,这个多边形是几边形?
解: 设这个多边形的边数为 n,根据题意,得
(n-2)·180°= 5× 360°.
解得 n = 12.
因此,这个多边形是十二变形.
已知一个多边形的每个内角与和它相邻的一个外角的比都是 7∶2,求这个多边形的边数.
解法一:设这个多边形的内角为 7x°,外角为 2x°,
根据题意得
7x + 2x = 180,
解得 x = 20.
即内角是 140°,外角是 40°.
360°÷40° = 9.
答:这个多边形的边数为 9.
还有其他解法吗?
解法二:设这个多边形的边数为 n ,根据题意得
解得 n = 9.
答:这个多边形的边数为 9.
1.一个多边形的每一个外角都等于45°,这个多边形是几边形?它的每一个内角是多少度?
2.在一个多边形中,
它的内角最多可以有几个是锐角?
1. 判断对错:
(1) 当多边形边数增加时,它的外角和也随着增加. ( )
(2) 三角形的外角和与八边形的外角和相等.( )
2. 一个多边形的所有内角与一个外角的和是 2380°,则这个多边形的边数为______.
15
解:设这个多边形的边数为 x ( x 为正整数),
则这个多边形的内角和为 ( x-2)×180°,由题意可得,
2380 -180 < (x-2)×180 < 2380,
解得 14.22 < x < 15.22
因为 x 为正整数,所以 x =15,即这个多边形的边数为15.
3. 如图,求图中 x 的值.
解:由题意可得,
3x+90+90 = 360.
解得 x = 60.
多边形的外角和
任意多边形的外角和都为360°
特别注意:与边数无关
定义
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
8.2 多边形的内角和与外角和
8.2.2 多边形的外角和
多边形的内角和
内角和计算公式
(n-2) × 180 °(n ≥ 3 的整数)
多边形的定义
由n条不在同一条直线上的线段首尾顺次连结组成的平面图形称为n边形,也即我们通常所说的多边形
如图,小刚每跑完一圈,身体转过的角度之和是多少?
与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角.
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
如图,∠1+∠2+∠3+∠4就是四边形ABCD的外角和.
从图中可以知道:
(∠1+∠5)+(∠2+∠6)+
(∠3+∠7)+(∠4+∠8) =4×180°,
所以 ∠1+∠2+∠3+∠4 = 4 × 180°-(∠5+∠6+∠7+∠8).
四边形ABCD的内角和为∠5+∠6+∠7+∠8=360°.
因此∠1+∠2+∠3+∠4=360°.
那么,
n边形的外角和应该等于多少度呢?
如图,从与每个内角相邻的两个外角中分别取一个:
1. 任意一个外角与和它相邻
的内角有什么关系?
2. 五个外角加上它们相邻的
五个内角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
5×180°= 900°
如图,从与每个内角相邻的两个外角中分别取一个:
3. 这五个平角和与五边形的内角和、外角和有什么关系?
E
B
C
D
1
2
3
4
5
A
五个平角和(900°)-五边形的内角和(540°)
=五边形的外角和(360°)
根据n边形的每一个内角与和它相邻的外角都互为补角,可以求得n边形的外角和.据此,请将数据填入表中.
360°
360°
360°
360°
360°
4×
180°
= 720°
5×
180°
= 900°
6×
180°
= 1080°
7×
180°
= 1260°
n×
180°
360°
540°
720°
900°
(n-2)
×180°
因此,任意多边形的外角和都为360°.
与 n 边形的每个内角相邻的外角分别有两个, 这两个外角是对顶角.
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为 n 边形的外角和.
n 边形外角和
-(n-2) × 180°
=360 °
= n 个平角和-n 边形内角和
= n×180 °
即,n边形的外角和等于360度.
例3 一个多边形的每个外角都是72°,这个多边形是几边形?
解: 设这个多边形的边数为 n,根据题意,得
n·72°=360°.
解得 n = 5.
因此,这个多边形是五边形.
例4 一个多边形的内角和等于它外角和的 5 倍,这个多边形是几边形?
解: 设这个多边形的边数为 n,根据题意,得
(n-2)·180°= 5× 360°.
解得 n = 12.
因此,这个多边形是十二变形.
已知一个多边形的每个内角与和它相邻的一个外角的比都是 7∶2,求这个多边形的边数.
解法一:设这个多边形的内角为 7x°,外角为 2x°,
根据题意得
7x + 2x = 180,
解得 x = 20.
即内角是 140°,外角是 40°.
360°÷40° = 9.
答:这个多边形的边数为 9.
还有其他解法吗?
解法二:设这个多边形的边数为 n ,根据题意得
解得 n = 9.
答:这个多边形的边数为 9.
1.一个多边形的每一个外角都等于45°,这个多边形是几边形?它的每一个内角是多少度?
2.在一个多边形中,
它的内角最多可以有几个是锐角?
1. 判断对错:
(1) 当多边形边数增加时,它的外角和也随着增加. ( )
(2) 三角形的外角和与八边形的外角和相等.( )
2. 一个多边形的所有内角与一个外角的和是 2380°,则这个多边形的边数为______.
15
解:设这个多边形的边数为 x ( x 为正整数),
则这个多边形的内角和为 ( x-2)×180°,由题意可得,
2380 -180 < (x-2)×180 < 2380,
解得 14.22 < x < 15.22
因为 x 为正整数,所以 x =15,即这个多边形的边数为15.
3. 如图,求图中 x 的值.
解:由题意可得,
3x+90+90 = 360.
解得 x = 60.
多边形的外角和
任意多边形的外角和都为360°
特别注意:与边数无关
定义
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和.
