8.3.2 用多种正多边形 课件(共36张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 8.3.2 用多种正多边形 课件(共36张PPT)2024-2025学年数学华师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 00:00:00 | ||
图片预览






文档简介
(共36张PPT)
8.3 用正多边形铺设地面
8.3.2 用多种正多边形
用相同的正多边形铺设地面
正多边形内、外角计算公式
相同正多边形铺满地面条件
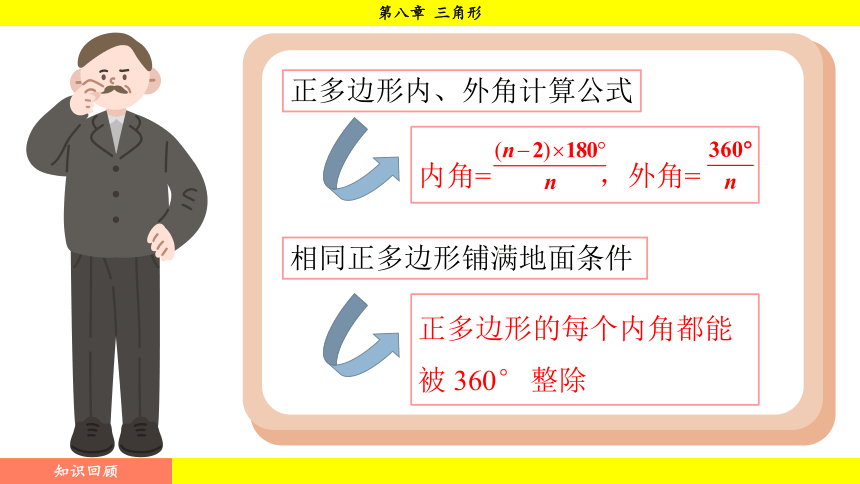
正多边形内、外角计算公式
正多边形的每个内角都能被 360° 整除
相同正多边形铺满地面条件
内角= ,外角=
如图,用正三角形和正六边形也能铺满地面.类似的情况还有吗?
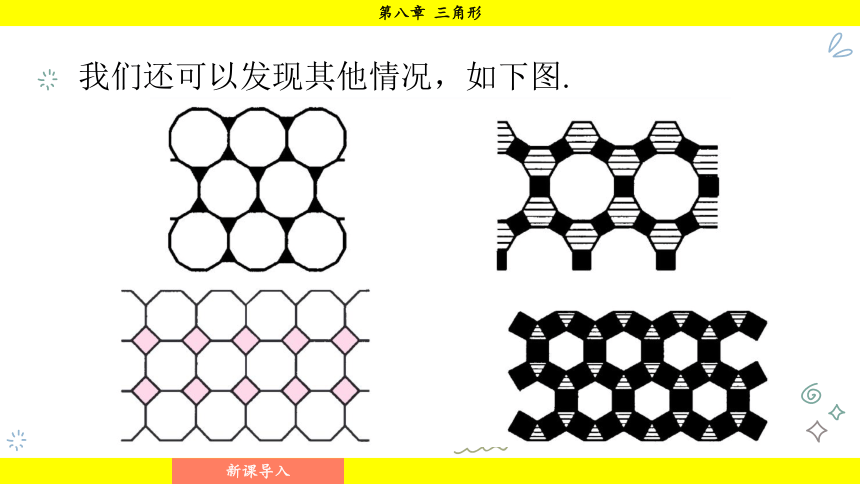
我们还可以发现其他情况,如下图.
现以右图为例,观察一下其中的关系.
正十二边形的一个内角为
=150°,正六边形的一个内角为120°,正方形的一个内角为90°,三者之和恰为一个周角360°.实际上,这三种正多边形结合在一起正好能铺满地面.
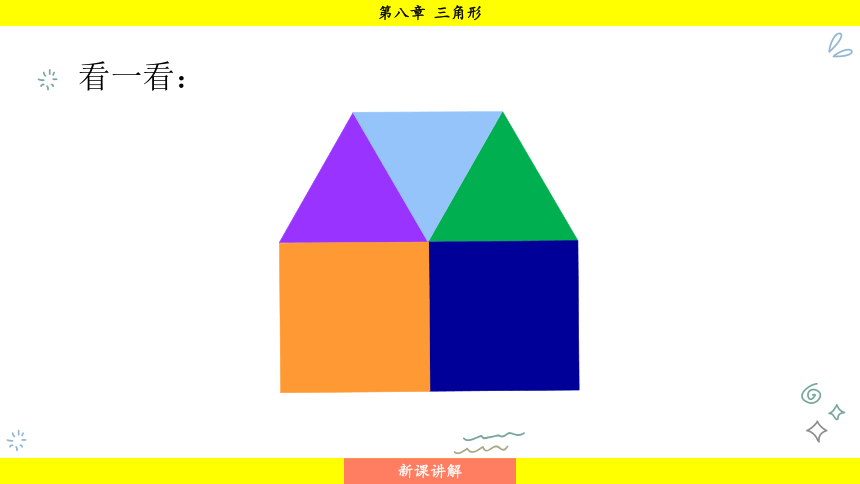
看一看:
问题 从正三角形、正方形、正五边形、正六边形、正八边形、正十边形、正十二边形中任取两种进行组合是否能铺满地面呢?
正方形、正三角形:
正六边形、正三角形:
正六边形、正方形、正三角形:
正十二边形、正三角形:
正八边形、正方形:
正五边形、正十边形:
围绕一点能拼成 360°,但能扩展到整个平面,即铺满地面吗?
尽管能围绕一点拼成 360 ,但不能扩展到整个平面。
正十二边形、正方形、正六边形:
正十二边形、正方形、正三角形:
关键:围绕一点拼在一起的多种正多边形的内角之和为 360 .
模型:
正多边形 1 的个数×正多边形 1 的内角度数 +正多边形 2 的个数×正多边形 2 的内角度数 +… = 360
多种正多边形铺设地面
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面。
如:正五边形与正十边形的组合.
多姿多彩的图案
我们已经看到了用正多边形拼成的各种图案.实际上,有许多图案是用规则或不规则的基本图形拼成的,如图1至图4.
图5和图6分别说明了相应的图案是如何由基本图形拼成的.
1.试说明本节中几种正多边形能铺满地面的理由.
2.任意剪出一些形状、大小相同的三角形纸板,拼拼看,它们能否铺满地面.
1. 现要选用两种不同的正多边形地砖铺地板,若选择了正四边形,则可以再选择的正多边形是( )
A. 正七边形 B. 正五边形
C. 正六边形 D. 正八边形
D
2. 用正三角形和正六边形铺成平面,共有不同的拼法是( )
A. 1个 B. 2个 C. 3个 D. 4个
B
围绕一点拼在一起的多种正多边形的内角之和为 360
用多种正多边形铺设地面
铺满地面的条件
8.3 用正多边形铺设地面
8.3.2 用多种正多边形
用相同的正多边形铺设地面
正多边形内、外角计算公式
相同正多边形铺满地面条件
正多边形内、外角计算公式
正多边形的每个内角都能被 360° 整除
相同正多边形铺满地面条件
内角= ,外角=
如图,用正三角形和正六边形也能铺满地面.类似的情况还有吗?
我们还可以发现其他情况,如下图.
现以右图为例,观察一下其中的关系.
正十二边形的一个内角为
=150°,正六边形的一个内角为120°,正方形的一个内角为90°,三者之和恰为一个周角360°.实际上,这三种正多边形结合在一起正好能铺满地面.
看一看:
问题 从正三角形、正方形、正五边形、正六边形、正八边形、正十边形、正十二边形中任取两种进行组合是否能铺满地面呢?
正方形、正三角形:
正六边形、正三角形:
正六边形、正方形、正三角形:
正十二边形、正三角形:
正八边形、正方形:
正五边形、正十边形:
围绕一点能拼成 360°,但能扩展到整个平面,即铺满地面吗?
尽管能围绕一点拼成 360 ,但不能扩展到整个平面。
正十二边形、正方形、正六边形:
正十二边形、正方形、正三角形:
关键:围绕一点拼在一起的多种正多边形的内角之和为 360 .
模型:
正多边形 1 的个数×正多边形 1 的内角度数 +正多边形 2 的个数×正多边形 2 的内角度数 +… = 360
多种正多边形铺设地面
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面。
如:正五边形与正十边形的组合.
多姿多彩的图案
我们已经看到了用正多边形拼成的各种图案.实际上,有许多图案是用规则或不规则的基本图形拼成的,如图1至图4.
图5和图6分别说明了相应的图案是如何由基本图形拼成的.
1.试说明本节中几种正多边形能铺满地面的理由.
2.任意剪出一些形状、大小相同的三角形纸板,拼拼看,它们能否铺满地面.
1. 现要选用两种不同的正多边形地砖铺地板,若选择了正四边形,则可以再选择的正多边形是( )
A. 正七边形 B. 正五边形
C. 正六边形 D. 正八边形
D
2. 用正三角形和正六边形铺成平面,共有不同的拼法是( )
A. 1个 B. 2个 C. 3个 D. 4个
B
围绕一点拼在一起的多种正多边形的内角之和为 360
用多种正多边形铺设地面
铺满地面的条件
