9.1.1 生活中的轴对称 课件(共34张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 9.1.1 生活中的轴对称 课件(共34张PPT)2024-2025学年数学华师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 22:22:11 | ||
图片预览







文档简介
(共34张PPT)
9.1 轴对称
9.1.1 生活中的轴对称
围绕一点拼在一起的多种正多边形的内角之和为 360
用多种正多边形铺设地面
铺满地面的条件
世界充满着运动,
从天体、
星球的运行,
到原子、粒子的作用,
其中最基本的是
轴对称、
平移、
旋转等运动.
轴对称、平移与旋转等合成了大千世界千姿百态的运动.
本章将探究在轴对称、平移与旋转的图形变化下图形的不变性质,并应用轴对称、平移与旋转等方法进行图案设计,从中体会图形变化在几何研究中的作用.
不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.
山倒映在湖中,这是令人难忘
的对称景象.自远古以来,对称的
形式都被认为是和谐美丽的.
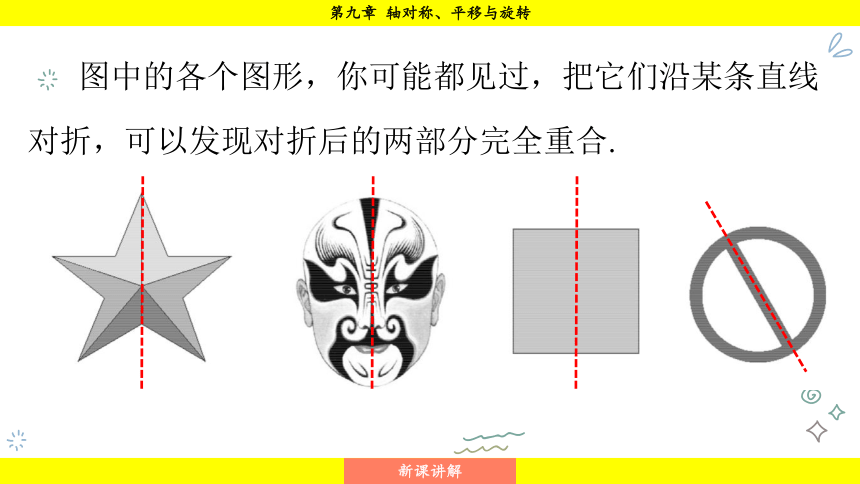
图中的各个图形,你可能都见过,把它们沿某条直线对折,可以发现对折后的两部分完全重合.
像这样的图形,叫做轴对称图形,
这条直线叫做这个图形的对称轴.
找出图中各图形的对称轴.是否有些图形的对称轴不止一条呢?
用一张半透明的纸描出图示的星形图,然后用不同的方式对折,用直尺画出折痕,
看看这幅星形图有多少条对称轴.
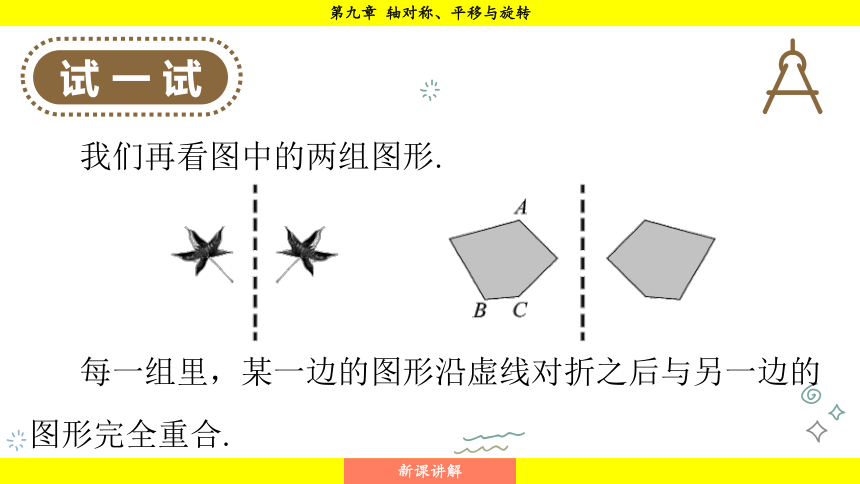
我们再看图中的两组图形.
每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.
像这样,把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,
这条直线叫做对称轴,
两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
你能举出日常生活中两个图形成轴对称的例子吗?
请你标出图中A、B、C三点的对称点A1、B1、C1 .
轴对称图形 两个图形成轴对称
图形
区别
联系
有特殊位置关系的两个相同图形
1. 都是沿着某条直线折叠后能重合;
2. 可以通过分割或整合互相转化.
具有特殊形状的一个图形
显然,轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的,所以
轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
这就是轴对称图形的基本特征.
1.下列图片中哪组图成轴对称?
B
C
A
...
2.找出各图形中的对称轴.
剪正五角星
节日前夕,有时需要制作许多
五角星.我们用折纸的方法,
可以直接剪出一个五角星.
方法是这样的:拿一张长方形(或圆形)的纸,对折成图1,再沿图1中的虚线将平角折成五等份,得到图2;
在五等份的折线上,取点A和点C,使OC比三分之一的OA微微长一点;沿斜线AC把图2中的阴影
部分剪掉,然后把纸展开,就得到图3
所示的一个正五角星.
如图4,若取得的OC比OA的三分之一长得多(如OC为OA的一半),这时剪出的
五角星就不一样了,它的
五个角的边比较短;
如图5,而当沿直角方向剪时,展开后则成了一个正五边形.
想一想:这种折纸剪正五角星
的方法,其中隐含着什么数学道理?
1.你一定见过许多美丽的照片或图片,如图所示的三幅图都给我们一种美妙和谐的轴对称形象.
现在请你尽可能多地找出类似的照片或图片,与你的同伴一起欣赏.
2.观察下列各种图形,分别判断是不是轴对称图形.
3.如图,已知正方形ABCD,点E、F、G、H分别是DA、AB、BC、CD的中点,四边形ABGE沿EG对折能与四边形DCGE重合,
D
H
C
E
G
A
F
B
点A的对称点是点 ;四边形 AFHD沿HF对折能与四边形BFHC重合,点B的对称点是点 .
D
H
C
E
G
A
F
B
1. 观察下列各种图形,判断是不是轴对称图形.
A C D E F G H I J L M N O P Q R S T U V W X Y Z
2. 下列英文字母中,哪些是轴对称图形?画出对称轴.
轴对称
轴对称图形
两个图形成轴对称
如果一个图形,把它沿着某条直线对折,对折后的两部分能完全重合,像这样的图形,叫做轴对称图形,这条直线叫做这个图形的对称轴.
轴对称图形定义
把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴.
两个图形成轴对称定义
区别
轴对称图形:具有特殊形状的一个图形
两个图形成轴对称:有着特殊位置关系的两个相同图形
9.1 轴对称
9.1.1 生活中的轴对称
围绕一点拼在一起的多种正多边形的内角之和为 360
用多种正多边形铺设地面
铺满地面的条件
世界充满着运动,
从天体、
星球的运行,
到原子、粒子的作用,
其中最基本的是
轴对称、
平移、
旋转等运动.
轴对称、平移与旋转等合成了大千世界千姿百态的运动.
本章将探究在轴对称、平移与旋转的图形变化下图形的不变性质,并应用轴对称、平移与旋转等方法进行图案设计,从中体会图形变化在几何研究中的作用.
不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.
山倒映在湖中,这是令人难忘
的对称景象.自远古以来,对称的
形式都被认为是和谐美丽的.
图中的各个图形,你可能都见过,把它们沿某条直线对折,可以发现对折后的两部分完全重合.
像这样的图形,叫做轴对称图形,
这条直线叫做这个图形的对称轴.
找出图中各图形的对称轴.是否有些图形的对称轴不止一条呢?
用一张半透明的纸描出图示的星形图,然后用不同的方式对折,用直尺画出折痕,
看看这幅星形图有多少条对称轴.
我们再看图中的两组图形.
每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.
像这样,把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,
这条直线叫做对称轴,
两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
你能举出日常生活中两个图形成轴对称的例子吗?
请你标出图中A、B、C三点的对称点A1、B1、C1 .
轴对称图形 两个图形成轴对称
图形
区别
联系
有特殊位置关系的两个相同图形
1. 都是沿着某条直线折叠后能重合;
2. 可以通过分割或整合互相转化.
具有特殊形状的一个图形
显然,轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的,所以
轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
这就是轴对称图形的基本特征.
1.下列图片中哪组图成轴对称?
B
C
A
...
2.找出各图形中的对称轴.
剪正五角星
节日前夕,有时需要制作许多
五角星.我们用折纸的方法,
可以直接剪出一个五角星.
方法是这样的:拿一张长方形(或圆形)的纸,对折成图1,再沿图1中的虚线将平角折成五等份,得到图2;
在五等份的折线上,取点A和点C,使OC比三分之一的OA微微长一点;沿斜线AC把图2中的阴影
部分剪掉,然后把纸展开,就得到图3
所示的一个正五角星.
如图4,若取得的OC比OA的三分之一长得多(如OC为OA的一半),这时剪出的
五角星就不一样了,它的
五个角的边比较短;
如图5,而当沿直角方向剪时,展开后则成了一个正五边形.
想一想:这种折纸剪正五角星
的方法,其中隐含着什么数学道理?
1.你一定见过许多美丽的照片或图片,如图所示的三幅图都给我们一种美妙和谐的轴对称形象.
现在请你尽可能多地找出类似的照片或图片,与你的同伴一起欣赏.
2.观察下列各种图形,分别判断是不是轴对称图形.
3.如图,已知正方形ABCD,点E、F、G、H分别是DA、AB、BC、CD的中点,四边形ABGE沿EG对折能与四边形DCGE重合,
D
H
C
E
G
A
F
B
点A的对称点是点 ;四边形 AFHD沿HF对折能与四边形BFHC重合,点B的对称点是点 .
D
H
C
E
G
A
F
B
1. 观察下列各种图形,判断是不是轴对称图形.
A C D E F G H I J L M N O P Q R S T U V W X Y Z
2. 下列英文字母中,哪些是轴对称图形?画出对称轴.
轴对称
轴对称图形
两个图形成轴对称
如果一个图形,把它沿着某条直线对折,对折后的两部分能完全重合,像这样的图形,叫做轴对称图形,这条直线叫做这个图形的对称轴.
轴对称图形定义
把一个图形沿着某一条直线对折,如果它能与另一个图形完全重合,那么就说这两个图形成轴对称,这条直线叫做对称轴.
两个图形成轴对称定义
区别
轴对称图形:具有特殊形状的一个图形
两个图形成轴对称:有着特殊位置关系的两个相同图形
