9.2.2 平移的特征 课件(共25张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 9.2.2 平移的特征 课件(共25张PPT)2024-2025学年数学华师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 938.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 22:25:54 | ||
图片预览






文档简介
(共25张PPT)
9.2 平移
9.2.2 平移的特征
图形的平移
平移的概念
相关概念
平面图形在它所在的平面上的平行移动,简称为平移.它是由移动方向和距离所决定
(1)对应点
(2)对应线段
(3)对应角
平面图形在它所在的平面上的平行移动,简称为平移.
平移不改变图形的形状、大小,只改变图形的位置.它由移动的方向和距离决定.
A
B
C
D
A′
B′
C′
D′
如图,在画平行线的时候,有时为了需要,将直尺和三角板放在倾斜的位置上.但不管怎样,我们总可以推得
A'B'//AB,A'B'=AB,∠B'=∠B.
同时也有
A'C' // ,A'C'= ,∠C'= .
B'C'与BC ,B'C'= ,∠A'= .
由此我们可以得到图形平移的特征:
平移后的图形与原来图形的对应线段平行
(或在同一条直线上)且相等,对应角相等,
图形的形状和大小不变.
在平移过程中,对应线段也可能在同一条直线上(如图B'C'与BC).
1. 平移后的图形与原来图形的对应线段平行且相等,对应角相等;
3. 在平移过程中,对应线段也可能在同一条直线上;
2. 平移后图形的形状和大小不变;
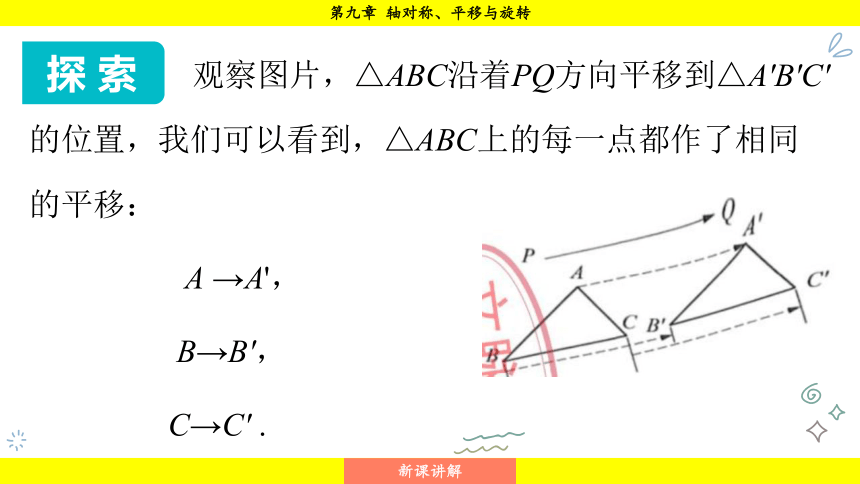
观察图片,△ABC沿着PQ方向平移到△A'B'C'的位置,我们可以看到,△ABC上的每一点都作了相同的平移:
A →A',
B→B',
C→C' .
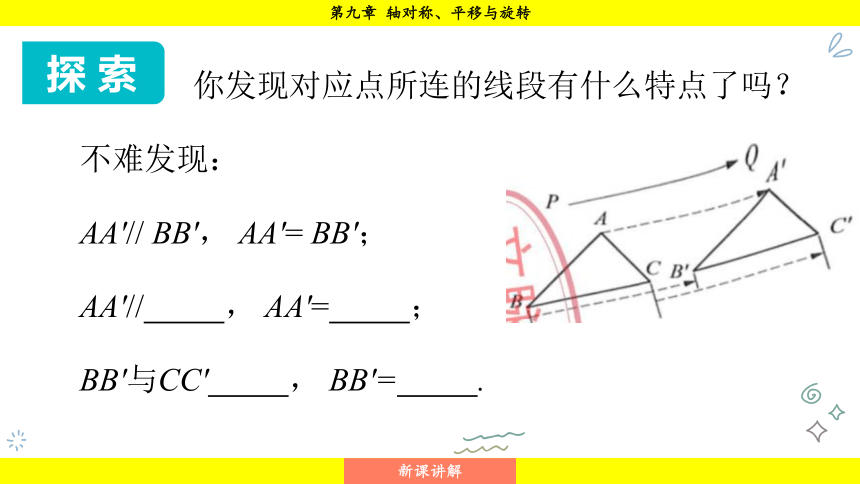
你发现对应点所连的线段有什么特点了吗?
不难发现:
AA'// BB', AA'= BB';
AA'// , AA'= ;
BB'与CC' , BB'= .
由此我们还可以得到:
平移后对应点所连的线段平行(或在同一条直线上)且相等.
在平移过程中,对应点所连的线段也可能在同一条直线上(如图BB'和CC').
将图中的△ABC沿PQ方向平移到△A'B'C'的位置,其平移的距离为线段PQ的长度.
观察所得到的对应线段和对应点
所连的线段是否符合上述我们所得到
的平移的特征?
例 如图,△ABC经过平移到达△A'B'C'的位置.指出平移的方向,并量出平移的距离.(精确到1mm)
解 由于点A与点A'是一对对应点,因此,如图,连结 AA',平移的方向就是点A到
点 A'的方向,平移的距离就
是线段 AA'的长,经测量可知,
约25mm.
在如图的方格图中,作出将图中的△ABC 向右平移4格后的△A'B'C',然后再作出
将△A'B'C'向上平移3格后的
△A"B"C".
△A"B"C"是否可以看成是△ABC经过一次平移而得到的?如果是,请指出平移
的方向和距离.
如图,在纸上作△ABC和平行直线m、n.作出△ABC关于直线m对称的△A'B'C',再作出
△A'B'C'关于直线n对称的
△A"B"C".
观察△ABC和△A"B"C",你能发现这两个三角形有什么关系吗?
在图形平移中,下面说法错误的是 ( )
A. 此图形上任意点移动的方向相同
B. 此图形上任意点移动的距离相等
C. 此图形上任意两点的连线的长度不变
D. 此图形上可能存在不动点
D
1.如图,在长方形ABCD中,对角线AC与BD相交于点O,画出△AOB平移后的三角形,其平移方向为射线AD的方向,平移的距离为线段AD的长.
2.先将方格图中的图形向左平移5格,然后再向下平移3格,作出平移后的图形.
3.将所给图形沿着PQ方向平移,平移距离为线段PQ的长,作出平移后的图形.
1. 经过平移,对应点所连的线段 ( )
A. 平行 (或在同一条直线上)
B. 相等
C. 平行 (或在同一条直线上) 且相等
D. 既不平行,又不相等
C
2. 右图中,可以视为是图形平移的对数(一个梅花对另一个梅花不计方向)有 ( )
A. 5 对 B. 8 对
C. 9 对 D. 10 对
D
平移的特征
平移后的图形与原来图形的对应线段平行并且相等,对应角相等,图形的形状与大小不变
对应点平移后对应点所连的线段平行并且相等
9.2 平移
9.2.2 平移的特征
图形的平移
平移的概念
相关概念
平面图形在它所在的平面上的平行移动,简称为平移.它是由移动方向和距离所决定
(1)对应点
(2)对应线段
(3)对应角
平面图形在它所在的平面上的平行移动,简称为平移.
平移不改变图形的形状、大小,只改变图形的位置.它由移动的方向和距离决定.
A
B
C
D
A′
B′
C′
D′
如图,在画平行线的时候,有时为了需要,将直尺和三角板放在倾斜的位置上.但不管怎样,我们总可以推得
A'B'//AB,A'B'=AB,∠B'=∠B.
同时也有
A'C' // ,A'C'= ,∠C'= .
B'C'与BC ,B'C'= ,∠A'= .
由此我们可以得到图形平移的特征:
平移后的图形与原来图形的对应线段平行
(或在同一条直线上)且相等,对应角相等,
图形的形状和大小不变.
在平移过程中,对应线段也可能在同一条直线上(如图B'C'与BC).
1. 平移后的图形与原来图形的对应线段平行且相等,对应角相等;
3. 在平移过程中,对应线段也可能在同一条直线上;
2. 平移后图形的形状和大小不变;
观察图片,△ABC沿着PQ方向平移到△A'B'C'的位置,我们可以看到,△ABC上的每一点都作了相同的平移:
A →A',
B→B',
C→C' .
你发现对应点所连的线段有什么特点了吗?
不难发现:
AA'// BB', AA'= BB';
AA'// , AA'= ;
BB'与CC' , BB'= .
由此我们还可以得到:
平移后对应点所连的线段平行(或在同一条直线上)且相等.
在平移过程中,对应点所连的线段也可能在同一条直线上(如图BB'和CC').
将图中的△ABC沿PQ方向平移到△A'B'C'的位置,其平移的距离为线段PQ的长度.
观察所得到的对应线段和对应点
所连的线段是否符合上述我们所得到
的平移的特征?
例 如图,△ABC经过平移到达△A'B'C'的位置.指出平移的方向,并量出平移的距离.(精确到1mm)
解 由于点A与点A'是一对对应点,因此,如图,连结 AA',平移的方向就是点A到
点 A'的方向,平移的距离就
是线段 AA'的长,经测量可知,
约25mm.
在如图的方格图中,作出将图中的△ABC 向右平移4格后的△A'B'C',然后再作出
将△A'B'C'向上平移3格后的
△A"B"C".
△A"B"C"是否可以看成是△ABC经过一次平移而得到的?如果是,请指出平移
的方向和距离.
如图,在纸上作△ABC和平行直线m、n.作出△ABC关于直线m对称的△A'B'C',再作出
△A'B'C'关于直线n对称的
△A"B"C".
观察△ABC和△A"B"C",你能发现这两个三角形有什么关系吗?
在图形平移中,下面说法错误的是 ( )
A. 此图形上任意点移动的方向相同
B. 此图形上任意点移动的距离相等
C. 此图形上任意两点的连线的长度不变
D. 此图形上可能存在不动点
D
1.如图,在长方形ABCD中,对角线AC与BD相交于点O,画出△AOB平移后的三角形,其平移方向为射线AD的方向,平移的距离为线段AD的长.
2.先将方格图中的图形向左平移5格,然后再向下平移3格,作出平移后的图形.
3.将所给图形沿着PQ方向平移,平移距离为线段PQ的长,作出平移后的图形.
1. 经过平移,对应点所连的线段 ( )
A. 平行 (或在同一条直线上)
B. 相等
C. 平行 (或在同一条直线上) 且相等
D. 既不平行,又不相等
C
2. 右图中,可以视为是图形平移的对数(一个梅花对另一个梅花不计方向)有 ( )
A. 5 对 B. 8 对
C. 9 对 D. 10 对
D
平移的特征
平移后的图形与原来图形的对应线段平行并且相等,对应角相等,图形的形状与大小不变
对应点平移后对应点所连的线段平行并且相等
