9.3.1 图形的旋转 课件(共24张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 9.3.1 图形的旋转 课件(共24张PPT)2024-2025学年数学华师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 22:26:05 | ||
图片预览






文档简介
(共24张PPT)
9.3 旋转
9.3.1 图形的旋转
平移的特征
平移后的图形与原来图形的对应线段平行并且相等,对应角相等,图形的形状与大小不变
对应点平移后对应点所连的线段平行并且相等
在日常生活中,除了物体的平行移动外,我们还可以看到许多物体的旋转现象.
时钟上秒针的不停转动
提醒着人们时间的流逝,
大风车的转动
给人们带来快乐,
飞速转动的电风扇叶片给人们带来丝丝凉意.
本章主要研究平面图形在一个平面上的旋转问题.
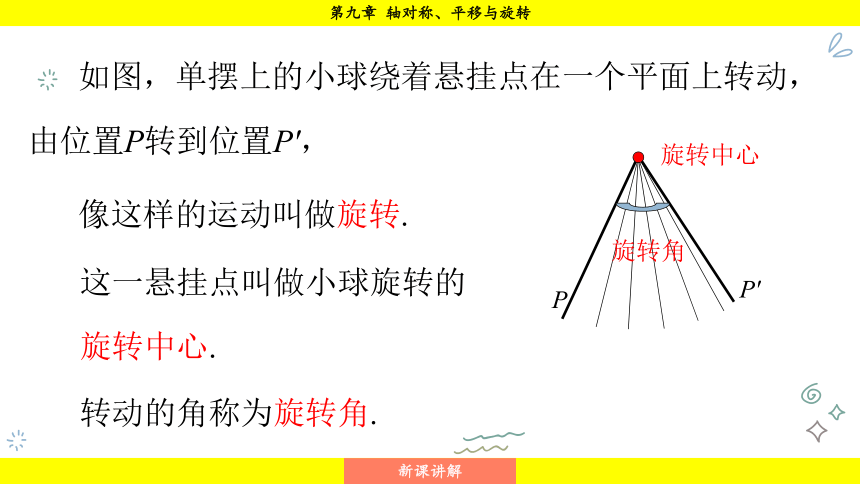
如图,单摆上的小球绕着悬挂点在一个平面上转动,由位置P转到位置P',
像这样的运动叫做旋转.
这一悬挂点叫做小球旋转的旋转中心.
旋转角
旋转中心
P
转动的角称为旋转角.
P'
显然,旋转中心在旋转过程中是保持不动的,
图形的旋转由旋转中心、
旋转角度和旋转方向决定.
旋转角
旋转中心
P
P'
把一张半透明的薄纸,覆盖在作有任意△AOB的纸上,在薄纸上作出与△AOB重合的一个三角形.
然后用一枚图钉在点O处固定,将
薄纸绕着图钉(即点O)逆时针旋转45°,
O
B
A
45°
薄纸上的三角形就旋转到了新的位置,
标上点A'、B',
我们可以认为△AOB逆时针旋转
45°后变成△A'OB'.
O
B
A
A'
B'
45°
D
D'
△AOB 的边 OB 的中点 D 的对应点在哪里?
在这样的旋转过程中,你发现了什么?
从图中,可以看到点A旋转到点A',OA
旋转到OA',∠AOB旋转到∠A'OB',
这些分别是互相对应的点、线段和角.
图形旋转时,必须注意旋转中心、旋转角度和旋转方向.
O
B
A
A'
B'
45°
D
D'
此时:点 B 的对应点是点_____;线段 OB 的对应线段是线段______;线段 AB 的对应线段是线
段______;∠A 的对应角是_______;∠B 的
对应角是_______;旋转中心是点______;
旋转角度是____________________.
B'
OB'
A'B'
∠A'
∠B'
O
∠BOB' 或者 ∠AOA'
O
B
A
A'
B'
45°
D
D'
例1 如图,△ABC 是等边三角形,D 是边 BC 上一点,△ABD 经过逆时针旋转后到达 △ACE 的位置.
(1) 旋转中心是哪一点?
(2) 旋转了多少度?
(3) 如果点 M 是 AB 的中点,那么
经过上述旋转后,点 M 转到了什么位置?
解 (1)旋转中心是点 A .
(2)旋转了60°.
(3)点 M 转到了 AC 的中点位置处.
例2 如图,点 M 是线段 AB 上一点,将线段 AB 绕着点 M 顺时针旋转 90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转 90°呢?
解 如图,顺时针旋转 90°,A'B' 与 AB 互相垂直.
逆时针旋转 90°,A''B'' 与 AB 互相垂直.
线段绕线段上的某一点旋转90°后与原来位置的线段互相垂直.
图形的旋转在图案设计中也具有广泛应用.如图所示的两幅美丽的图案都可以看成是由一个或几个基本图案,在同一平面上旋转若干次而产生的结果.
1.举出现实生活中旋转的一些实例.
2.如图,△ABC按逆时针方向旋转一个角度后成为△AB'C',图中哪一点是旋转中心?旋转了多少度?
3.如图,△ABC和△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在边AB上,如果△ABC经逆时针旋转后能与
△ADE重合,那么哪一点是
旋转中心?旋转了多少度?
1.若叶片 A 绕 O 顺时针旋转到叶片 B,则旋转中心是___,旋转角是_______,旋转角等于____°,其中的对应点有
_______、_______、_______、
_______、_______、_______.
O
∠AOB
60
F 与 A
A 与 B
B 与 C
C 与 D
D 与 E
E 与 F
A
C
D
E
F
B
O
2. △A′ OB′ 是 △AOB 绕点 O 按逆时针方向旋转得到的。已知 ∠AOB=20 °,∠ A ′ OB =24°,AB=3,OA=5,则A′ B′ = ,OA ′ = ,旋转角等于 .
3
5
44 °
旋转中心
旋转角
旋转方向
图形的旋转
旋转的概念
旋转图形前后比较
对应角
对应点
对应线段
9.3 旋转
9.3.1 图形的旋转
平移的特征
平移后的图形与原来图形的对应线段平行并且相等,对应角相等,图形的形状与大小不变
对应点平移后对应点所连的线段平行并且相等
在日常生活中,除了物体的平行移动外,我们还可以看到许多物体的旋转现象.
时钟上秒针的不停转动
提醒着人们时间的流逝,
大风车的转动
给人们带来快乐,
飞速转动的电风扇叶片给人们带来丝丝凉意.
本章主要研究平面图形在一个平面上的旋转问题.
如图,单摆上的小球绕着悬挂点在一个平面上转动,由位置P转到位置P',
像这样的运动叫做旋转.
这一悬挂点叫做小球旋转的旋转中心.
旋转角
旋转中心
P
转动的角称为旋转角.
P'
显然,旋转中心在旋转过程中是保持不动的,
图形的旋转由旋转中心、
旋转角度和旋转方向决定.
旋转角
旋转中心
P
P'
把一张半透明的薄纸,覆盖在作有任意△AOB的纸上,在薄纸上作出与△AOB重合的一个三角形.
然后用一枚图钉在点O处固定,将
薄纸绕着图钉(即点O)逆时针旋转45°,
O
B
A
45°
薄纸上的三角形就旋转到了新的位置,
标上点A'、B',
我们可以认为△AOB逆时针旋转
45°后变成△A'OB'.
O
B
A
A'
B'
45°
D
D'
△AOB 的边 OB 的中点 D 的对应点在哪里?
在这样的旋转过程中,你发现了什么?
从图中,可以看到点A旋转到点A',OA
旋转到OA',∠AOB旋转到∠A'OB',
这些分别是互相对应的点、线段和角.
图形旋转时,必须注意旋转中心、旋转角度和旋转方向.
O
B
A
A'
B'
45°
D
D'
此时:点 B 的对应点是点_____;线段 OB 的对应线段是线段______;线段 AB 的对应线段是线
段______;∠A 的对应角是_______;∠B 的
对应角是_______;旋转中心是点______;
旋转角度是____________________.
B'
OB'
A'B'
∠A'
∠B'
O
∠BOB' 或者 ∠AOA'
O
B
A
A'
B'
45°
D
D'
例1 如图,△ABC 是等边三角形,D 是边 BC 上一点,△ABD 经过逆时针旋转后到达 △ACE 的位置.
(1) 旋转中心是哪一点?
(2) 旋转了多少度?
(3) 如果点 M 是 AB 的中点,那么
经过上述旋转后,点 M 转到了什么位置?
解 (1)旋转中心是点 A .
(2)旋转了60°.
(3)点 M 转到了 AC 的中点位置处.
例2 如图,点 M 是线段 AB 上一点,将线段 AB 绕着点 M 顺时针旋转 90°,旋转后的线段与原线段的位置有何关系?如果逆时针旋转 90°呢?
解 如图,顺时针旋转 90°,A'B' 与 AB 互相垂直.
逆时针旋转 90°,A''B'' 与 AB 互相垂直.
线段绕线段上的某一点旋转90°后与原来位置的线段互相垂直.
图形的旋转在图案设计中也具有广泛应用.如图所示的两幅美丽的图案都可以看成是由一个或几个基本图案,在同一平面上旋转若干次而产生的结果.
1.举出现实生活中旋转的一些实例.
2.如图,△ABC按逆时针方向旋转一个角度后成为△AB'C',图中哪一点是旋转中心?旋转了多少度?
3.如图,△ABC和△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在边AB上,如果△ABC经逆时针旋转后能与
△ADE重合,那么哪一点是
旋转中心?旋转了多少度?
1.若叶片 A 绕 O 顺时针旋转到叶片 B,则旋转中心是___,旋转角是_______,旋转角等于____°,其中的对应点有
_______、_______、_______、
_______、_______、_______.
O
∠AOB
60
F 与 A
A 与 B
B 与 C
C 与 D
D 与 E
E 与 F
A
C
D
E
F
B
O
2. △A′ OB′ 是 △AOB 绕点 O 按逆时针方向旋转得到的。已知 ∠AOB=20 °,∠ A ′ OB =24°,AB=3,OA=5,则A′ B′ = ,OA ′ = ,旋转角等于 .
3
5
44 °
旋转中心
旋转角
旋转方向
图形的旋转
旋转的概念
旋转图形前后比较
对应角
对应点
对应线段
