9.4 中心对称 课件(共50张PPT)2024-2025学年数学华师大版七年级下册
文档属性
| 名称 | 9.4 中心对称 课件(共50张PPT)2024-2025学年数学华师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 22:30:15 | ||
图片预览







文档简介
(共50张PPT)
9.4 中心对称
定义
与轴对称图形的区别
画法
旋转对称图形
定义:
在平面内,将一个图形绕着一定点旋转一定角度(小于周角)后能与自身重合的图形叫做旋转对称图形.
旋转的度数称为旋转角度.一般来说,旋转角度可以多个,旋转中心只有一个.
与轴对称图形的区别:
1. 是两种不同的对称图形,旋转对称图形不一定是轴对称图形,轴对称图形不一定是旋转对称图形,它们是两个不同的概念.
2. 旋转对称图形是旋转一定的角度得到,轴对称图形是翻折得到.
画法:
1. 任意定一点旋转中心 O;
2. 按设计需要,把周角 360°分成n等份;
3. 以 O 为旋转中心,360°除以 n 的商为旋转角做顺时针或逆时针旋转 n-1次即可得到一个旋转对称图形.
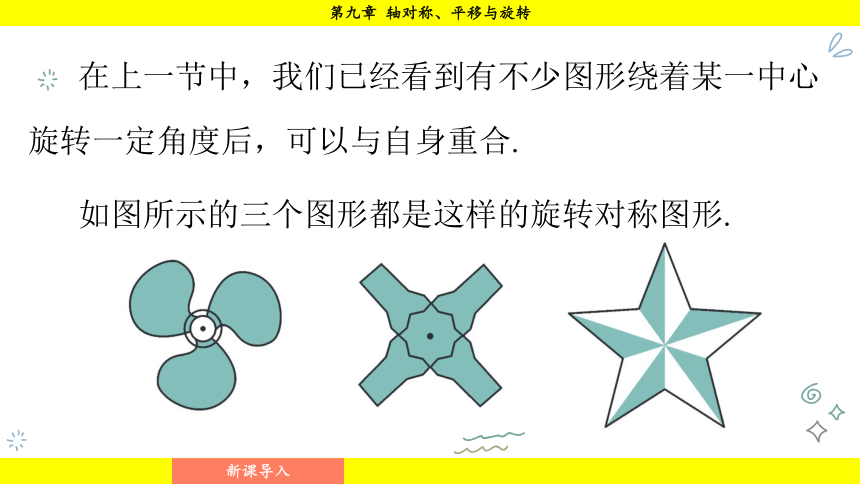
在上一节中,我们已经看到有不少图形绕着某一中心旋转一定角度后,可以与自身重合.
如图所示的三个图形都是这样的旋转对称图形.
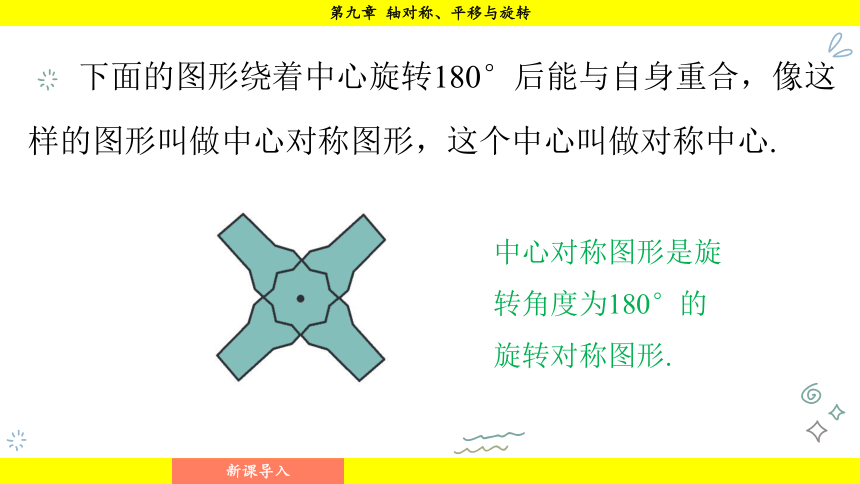
下面的图形绕着中心旋转180°后能与自身重合,像这样的图形叫做中心对称图形,这个中心叫做对称中心.
中心对称图形是旋转角度为180°的旋转对称图形.
中心对称图形:
将下面的图形绕 O 点旋转,你有什么发现?
A
B
O
O
(1) 都绕一点旋转了180°;
(2) 都与原图形完全重合.
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么,我们就说这两个图形成中心对称,
这个点叫做对称中心,
这两个图形中的对应点叫做关于中心的对称点.
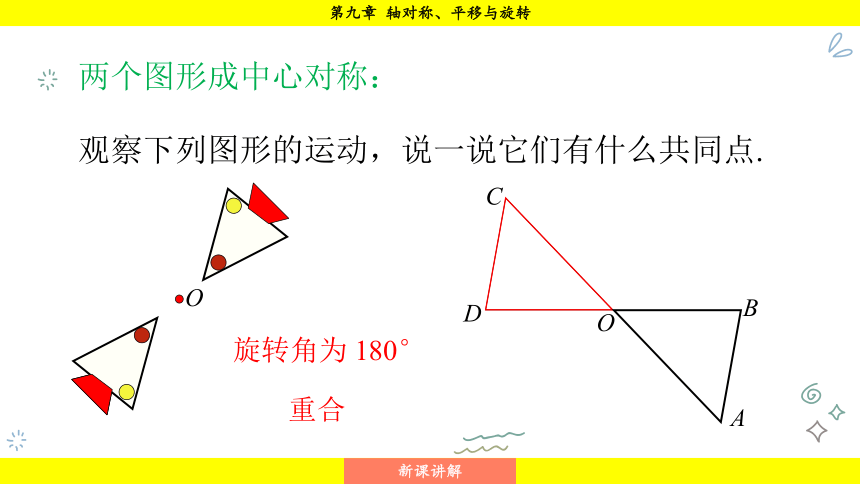
两个图形成中心对称:
观察下列图形的运动,说一说它们有什么共同点.
重合
O
A
D
B
C
旋转角为 180°
O
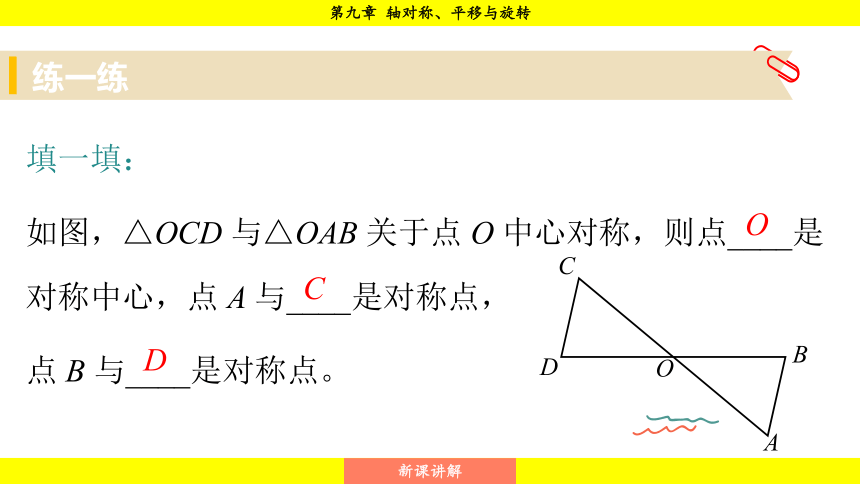
填一填:
如图,△OCD 与△OAB 关于点 O 中心对称,则点____是对称中心,点 A 与____是对称点,
点 B 与____是对称点。
O
B
C
A
D
O
C
D
线段、等边三角形、平行四边形、长方形、正方形、圆分别是中心对称图形吗?
如果是,那么对称中心又分别在哪里?
如图所示,△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,
点B的对称点为点 ,
点C的对称点为点 ,
点A的对称点为点 .
点B绕着点A旋转180°到达点D处,
因此,B、A、D三点在同一条直线上,
并且AB=AD.
C、A、E三点的位置关系怎样?
线段AC、AE的大小关系呢?
在图中,△A'B'C'与△ABC关于点O成中心对称,你能从图中找到哪些等量关系?
我们可以发现,点A绕中心点O旋转180°后到点A',于是A、O、A'三点在同一条直线上,
并且OA=OA'.另外分别在同一条直线上的
三点还有 和 ;
并且OB= ,OC= .
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
例 如图,已知△ABC和点O,作△DEF,使△DEF与△ABC关于点O成中心对称.
作法 (1)连结AO并延长AO到点D,使OD=OA,于是得到点A关于点O的对称点D;
(2)同样作出点B和点C关于点O的对称点E和点F;
(3)顺次连结DE、EF、FD.
如图,△DEF即为所要求
作的三角形.
如图,已知 △ABC 与 △A′B′C′ 中心对称,找出它们的对称中心 O.
A
B
C
A′
B′
C′
解法1:根据观察,B、B′ 应是对应点,连接 BB′,用刻度尺找出 BB′ 的中点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
解法 2:根据观察,B、B′ 及 C、C′ 应是两组对应点,连接 BB′、CC′,BB′、CC′ 相交于点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
注意:如果限制只用直尺作图,就用解法 2.
对弈策略
两个人轮流在一张桌面(长方形、正方形或圆形)上摆放同样大小的硬币,规则是:每人每次摆一个,硬币不能相互重叠,也不能有一部分在桌面边沿之外,摆好
以后不准移动,这样经过多次摆放,直到谁最先摆不下
硬币,谁就认输.按照这个规则,你用什么办法才能取胜?
初看起来,只能碰运气,其实不然,只要你先摆,并且采取中心对称策略,你就一定能取胜.取胜的秘诀是:
你先把一枚硬币放在桌面的对称中心上,以后根据对方所放硬币的位置,在它关于中心对称的位置上放下一枚硬币.这样,由于对称性,只要对方能放下一枚硬币,你就能在其对称的位置上放下一枚硬币.你不妨试一试.
如图所示的两个图形成中心对称,你能找到它们的对称中心吗?
小明找到了如图所示的方法,你呢?你知道其中的理由吗?你还能找到其他方法吗
如图,在纸上作△ABC和点O,以及过点O的任意两条互相垂直的直线x、y,
作出△ABC关于直线x对称的
△A'B'C',再作出△A'B'C'关于
直线y对称的△A"B"C" .
观察△ABC和△A"B"C" ,你能发现这两个三角形有什么关系吗?
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
1.仔细观察如图所示的26个英文字母,将相应的字母填入表中适当的空格内.
2.如图,四边形ABCD是长方形,AB>BC.
这个长方形是轴对称图形吗?如果是,请作出它的对称轴.它的对称轴有几条?
这个长方形是中心对称图形吗?如果是,请作出它的对称中心.这个长方形是旋转对称图形吗?如果是,那么这个长方形绕哪一点旋转多少度后能与自身重合?
3.如图所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼晴,请一位观众上台,把某一张牌旋转180°.
魔术师解除蒙具后,看到4张扑克牌如图所示,他很快确定了哪一张牌被旋转过.你能确定吗?
4.如图,已知四边形ABCD和点O,画四边形A'B'C'D',使四边形A'B'C'D'和四边形ABCD关于点O成中心对称.
5.如图,已知点P是△ABC内一点,作出△ABC关于点P成中心对称的△A'B'C'.
6.如图,先在纸上作△ABC和点P,再作出△ABC关于点P成中心对称的△A'B'C'.
在此基础上,再过点P任意作一条直线,作出△ABC关于此直线对称的△A"B"C".观察△A'B'C'和△A"B"C",你发现了什么?
1. 判断正误:
(1)轴对称的两个图形一定是相同图形,但相同的两个图形不一定是轴对称的图形。( )
(2)成中心对称的两个图形一定是相同图形,但相同的两个图形不一定是成中心对称的图形。 ( )
√
√
(3)相同的两个图形,不是成中心对称的图形,就是成轴对称的图形。 ( )
×
2. 如下所示的 4 组图形中,左边数字与右边数字成中心对称的有( )
A. 1 组 B. 2 组 C. 3 组 D. 4 组
C
3. 如图,已知 △AOB 与 △DOC 成中心对称,△AOB 的面积是 6,AB=3,则△DOC 中 CD边上的高是( )
A. 2 B. 4
C. 6 D. 8
A
B
C
D
O
B
4. 如图,已知等边三角形 ABC 和点 O,画△A′B′C′,
使△A′B′C′ 和 △ABC 关于点 O 成中心对称。
A′
B′
C′
O
A
B
C
中心对称
中心对称图形
两个图形成中心对称
中心对称图形
一个图形绕着中心旋转180°后能与自身重合,像这样的图形叫做中心对称图形.
两个图形成中心对称
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么,我们就说这两个图形成中心对称.
9.4 中心对称
定义
与轴对称图形的区别
画法
旋转对称图形
定义:
在平面内,将一个图形绕着一定点旋转一定角度(小于周角)后能与自身重合的图形叫做旋转对称图形.
旋转的度数称为旋转角度.一般来说,旋转角度可以多个,旋转中心只有一个.
与轴对称图形的区别:
1. 是两种不同的对称图形,旋转对称图形不一定是轴对称图形,轴对称图形不一定是旋转对称图形,它们是两个不同的概念.
2. 旋转对称图形是旋转一定的角度得到,轴对称图形是翻折得到.
画法:
1. 任意定一点旋转中心 O;
2. 按设计需要,把周角 360°分成n等份;
3. 以 O 为旋转中心,360°除以 n 的商为旋转角做顺时针或逆时针旋转 n-1次即可得到一个旋转对称图形.
在上一节中,我们已经看到有不少图形绕着某一中心旋转一定角度后,可以与自身重合.
如图所示的三个图形都是这样的旋转对称图形.
下面的图形绕着中心旋转180°后能与自身重合,像这样的图形叫做中心对称图形,这个中心叫做对称中心.
中心对称图形是旋转角度为180°的旋转对称图形.
中心对称图形:
将下面的图形绕 O 点旋转,你有什么发现?
A
B
O
O
(1) 都绕一点旋转了180°;
(2) 都与原图形完全重合.
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么,我们就说这两个图形成中心对称,
这个点叫做对称中心,
这两个图形中的对应点叫做关于中心的对称点.
两个图形成中心对称:
观察下列图形的运动,说一说它们有什么共同点.
重合
O
A
D
B
C
旋转角为 180°
O
填一填:
如图,△OCD 与△OAB 关于点 O 中心对称,则点____是对称中心,点 A 与____是对称点,
点 B 与____是对称点。
O
B
C
A
D
O
C
D
线段、等边三角形、平行四边形、长方形、正方形、圆分别是中心对称图形吗?
如果是,那么对称中心又分别在哪里?
如图所示,△ABC与△ADE是成中心对称的两个三角形,点A是对称中心,
点B的对称点为点 ,
点C的对称点为点 ,
点A的对称点为点 .
点B绕着点A旋转180°到达点D处,
因此,B、A、D三点在同一条直线上,
并且AB=AD.
C、A、E三点的位置关系怎样?
线段AC、AE的大小关系呢?
在图中,△A'B'C'与△ABC关于点O成中心对称,你能从图中找到哪些等量关系?
我们可以发现,点A绕中心点O旋转180°后到点A',于是A、O、A'三点在同一条直线上,
并且OA=OA'.另外分别在同一条直线上的
三点还有 和 ;
并且OB= ,OC= .
在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形关于这一点成中心对称.
例 如图,已知△ABC和点O,作△DEF,使△DEF与△ABC关于点O成中心对称.
作法 (1)连结AO并延长AO到点D,使OD=OA,于是得到点A关于点O的对称点D;
(2)同样作出点B和点C关于点O的对称点E和点F;
(3)顺次连结DE、EF、FD.
如图,△DEF即为所要求
作的三角形.
如图,已知 △ABC 与 △A′B′C′ 中心对称,找出它们的对称中心 O.
A
B
C
A′
B′
C′
解法1:根据观察,B、B′ 应是对应点,连接 BB′,用刻度尺找出 BB′ 的中点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
解法 2:根据观察,B、B′ 及 C、C′ 应是两组对应点,连接 BB′、CC′,BB′、CC′ 相交于点 O,则点 O 即为所求(如图).
A
B
C
A′
B′
C′
O
注意:如果限制只用直尺作图,就用解法 2.
对弈策略
两个人轮流在一张桌面(长方形、正方形或圆形)上摆放同样大小的硬币,规则是:每人每次摆一个,硬币不能相互重叠,也不能有一部分在桌面边沿之外,摆好
以后不准移动,这样经过多次摆放,直到谁最先摆不下
硬币,谁就认输.按照这个规则,你用什么办法才能取胜?
初看起来,只能碰运气,其实不然,只要你先摆,并且采取中心对称策略,你就一定能取胜.取胜的秘诀是:
你先把一枚硬币放在桌面的对称中心上,以后根据对方所放硬币的位置,在它关于中心对称的位置上放下一枚硬币.这样,由于对称性,只要对方能放下一枚硬币,你就能在其对称的位置上放下一枚硬币.你不妨试一试.
如图所示的两个图形成中心对称,你能找到它们的对称中心吗?
小明找到了如图所示的方法,你呢?你知道其中的理由吗?你还能找到其他方法吗
如图,在纸上作△ABC和点O,以及过点O的任意两条互相垂直的直线x、y,
作出△ABC关于直线x对称的
△A'B'C',再作出△A'B'C'关于
直线y对称的△A"B"C" .
观察△ABC和△A"B"C" ,你能发现这两个三角形有什么关系吗?
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
1
A
B
C
C
1
A
B
1
O
中心对称与轴对称的异同
1.仔细观察如图所示的26个英文字母,将相应的字母填入表中适当的空格内.
2.如图,四边形ABCD是长方形,AB>BC.
这个长方形是轴对称图形吗?如果是,请作出它的对称轴.它的对称轴有几条?
这个长方形是中心对称图形吗?如果是,请作出它的对称中心.这个长方形是旋转对称图形吗?如果是,那么这个长方形绕哪一点旋转多少度后能与自身重合?
3.如图所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼晴,请一位观众上台,把某一张牌旋转180°.
魔术师解除蒙具后,看到4张扑克牌如图所示,他很快确定了哪一张牌被旋转过.你能确定吗?
4.如图,已知四边形ABCD和点O,画四边形A'B'C'D',使四边形A'B'C'D'和四边形ABCD关于点O成中心对称.
5.如图,已知点P是△ABC内一点,作出△ABC关于点P成中心对称的△A'B'C'.
6.如图,先在纸上作△ABC和点P,再作出△ABC关于点P成中心对称的△A'B'C'.
在此基础上,再过点P任意作一条直线,作出△ABC关于此直线对称的△A"B"C".观察△A'B'C'和△A"B"C",你发现了什么?
1. 判断正误:
(1)轴对称的两个图形一定是相同图形,但相同的两个图形不一定是轴对称的图形。( )
(2)成中心对称的两个图形一定是相同图形,但相同的两个图形不一定是成中心对称的图形。 ( )
√
√
(3)相同的两个图形,不是成中心对称的图形,就是成轴对称的图形。 ( )
×
2. 如下所示的 4 组图形中,左边数字与右边数字成中心对称的有( )
A. 1 组 B. 2 组 C. 3 组 D. 4 组
C
3. 如图,已知 △AOB 与 △DOC 成中心对称,△AOB 的面积是 6,AB=3,则△DOC 中 CD边上的高是( )
A. 2 B. 4
C. 6 D. 8
A
B
C
D
O
B
4. 如图,已知等边三角形 ABC 和点 O,画△A′B′C′,
使△A′B′C′ 和 △ABC 关于点 O 成中心对称。
A′
B′
C′
O
A
B
C
中心对称
中心对称图形
两个图形成中心对称
中心对称图形
一个图形绕着中心旋转180°后能与自身重合,像这样的图形叫做中心对称图形.
两个图形成中心对称
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么,我们就说这两个图形成中心对称.
