3.2.1 不等式的基本性质1、2 课件(共31张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 3.2.1 不等式的基本性质1、2 课件(共31张PPT)2024-2025学年数学湘教版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 16:25:51 | ||
图片预览









文档简介
(共31张PPT)
3.2 不等式的基本性质
3.2.1 不等式的基本性质1、2
水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果.
请用 “ >”或 “ <”填空:
100 – a 84 – a
100 – a+b 84 – a+b
>
>
已知2 < 3,先用“>”或“<”填空:
2+ 3+,2- 3-( ≈ 1.414),
再观察结果,由此可猜测出什么结论?
由于2 + = ,3 + = , < ,
所以2 + < 3 + .
由于2 - ≈ 0.586,3 - ≈ 1.586,
所以2 - < 3 - .
由此可猜测:若a,b,c都是实数,且a下面来说明这个猜测是真的.
设a,b,c都是实数.
若a(a+c)-(b+c)=a+c-b-c=a-b<0,
因此 a+c < b+c.
类似地,有a+(-c)若a>b,同理可得a+c>b+c,a-c>b-c.
类似地,可以证明:在不等式的两边都加上或减去同一个整式,不等号的方向不变.
+
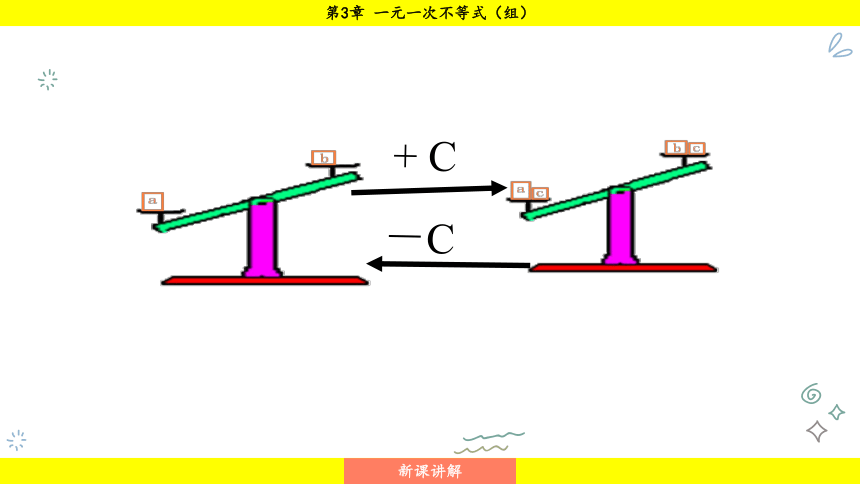
活动 用天平探究不等式的性质
+ C
-C
综上可得不等式的基本性质1:
不等式的两边都加上或减去同一个数(或同一个整式),不等号的方向不变.
即,如果a > b,那么a+c > b+c,a-c > b-c.
用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据______________;
(2)若a-2<3,则a______5,
根据______________.
>
<
不等式性质1
不等式性质1
解 (1)因为 a>b,根据不等式的基本性质1得,a + > b + .
(2)因为3<7,根据不等式的基本性质1得, 3-x<7-x.
(1)已知 a>b,则a+ b+;
(2)已知3<7,则3-x 7-x.
例1 用“>”或“<”填空:
>
<
关于不等式基本性质1的说明
以3x<2x-2为例,说明在不等式两边都加上或减去同一个整式,不等号方向不变.
不等式3x<2x-2的含义是:x用哪些实数代入,能够使得左边3x的值小于右边2x-2的值.
设x用实数a代入,能够使得左边的值小于右边的值,即3a<2a-2.
在不等式3a<2a-2的两边减去同一个实数2a,得a<-2.
显然,满足这一条件的所有实数a,也是使得不等式x<-2成立的所有实数.
于是不等式3x<2x-2可以变形成不等式x<-2,这相当于在3x<2x-2的两边都减去2x,并且不等号的方向不变.
已知苹果的价格是a元/kg,梨的价格是b元/kg,且a>b.
小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空:
3a 3b
>
已知3<5,先用“>”或“<”填空:
3π 5π, ,
再观察结果,由此可猜测出什么结论?
由于π ≈ 3.14,3π = 3×π ≈ 9.42,5π = 5×π ≈ 15.7,
于是 3π < 5π,.
由此猜测:若a,b,c都是实数,且a0,则ac下面来说明上述猜测是真的.
已知a又c>0,于是 (a-b)c<0,
从而有 ac-bc<0,
因此 ac又 > 0,同理可得 a· < b·,即
< .
对于实数a,b,c,若a > b,c > 0,类似地,可以得到
ac>bc, .
综上可得不等式的基本性质2 :
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即,如果a > b,c > 0,那么 ac > bc , > .
例2 用“>”或“<”填空:
(1)已知a(2)已知a>b,则 .
解 (1)因为a0,根据不等式的基本性质2得,
aπ(2)因为a>b,3>0,根据不等式的基本性质2得,
> .
>
<
例3 利用 >2,比较 与 的大小.
解 因为 >2,根据不等式的基本性质1得,
> 2-1,
即 >1.
又因为 >0,根据不等式的基本性质2得,
> .
1 已知3<π,用“>”或“<”填空:
(1)3+ π+; (2)1 π-2;
(3) ; (4) π.
<
<
<
<
2 已知a”或“<”填空:
(1)a+xy b+xy; (2)a-2x b-2x;
(3)5a 5b; (4) .
<
<
<
<
3 利用>6,比较 与 的大小.
1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b -10 a -10 .
<
>
因为 a>b,两边都乘3,
解:
由不等式基本性质2,得
3a > 3b.
已知 a>b,则3a 3b ;
>
2.用“>”或“<”填空:
3.2 不等式的基本性质
3.2.1 不等式的基本性质1、2
水果店的小王从水果批发市场购进100kg梨和84kg苹果. 在卖出a kg梨和a kg苹果后,又分别各购进了b kg的梨和苹果.
请用 “ >”或 “ <”填空:
100 – a 84 – a
100 – a+b 84 – a+b
>
>
已知2 < 3,先用“>”或“<”填空:
2+ 3+,2- 3-( ≈ 1.414),
再观察结果,由此可猜测出什么结论?
由于2 + = ,3 + = , < ,
所以2 + < 3 + .
由于2 - ≈ 0.586,3 - ≈ 1.586,
所以2 - < 3 - .
由此可猜测:若a,b,c都是实数,且a
设a,b,c都是实数.
若a
因此 a+c < b+c.
类似地,有a+(-c)
类似地,可以证明:在不等式的两边都加上或减去同一个整式,不等号的方向不变.
+
活动 用天平探究不等式的性质
+ C
-C
综上可得不等式的基本性质1:
不等式的两边都加上或减去同一个数(或同一个整式),不等号的方向不变.
即,如果a > b,那么a+c > b+c,a-c > b-c.
用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,
根据______________;
(2)若a-2<3,则a______5,
根据______________.
>
<
不等式性质1
不等式性质1
解 (1)因为 a>b,根据不等式的基本性质1得,a + > b + .
(2)因为3<7,根据不等式的基本性质1得, 3-x<7-x.
(1)已知 a>b,则a+ b+;
(2)已知3<7,则3-x 7-x.
例1 用“>”或“<”填空:
>
<
关于不等式基本性质1的说明
以3x<2x-2为例,说明在不等式两边都加上或减去同一个整式,不等号方向不变.
不等式3x<2x-2的含义是:x用哪些实数代入,能够使得左边3x的值小于右边2x-2的值.
设x用实数a代入,能够使得左边的值小于右边的值,即3a<2a-2.
在不等式3a<2a-2的两边减去同一个实数2a,得a<-2.
显然,满足这一条件的所有实数a,也是使得不等式x<-2成立的所有实数.
于是不等式3x<2x-2可以变形成不等式x<-2,这相当于在3x<2x-2的两边都减去2x,并且不等号的方向不变.
已知苹果的价格是a元/kg,梨的价格是b元/kg,且a>b.
小李各买了3kg苹果和梨,则买哪种水果花钱较多?
用不等号填空:
3a 3b
>
已知3<5,先用“>”或“<”填空:
3π 5π, ,
再观察结果,由此可猜测出什么结论?
由于π ≈ 3.14,3π = 3×π ≈ 9.42,5π = 5×π ≈ 15.7,
于是 3π < 5π,.
由此猜测:若a,b,c都是实数,且a
已知a
从而有 ac-bc<0,
因此 ac
< .
对于实数a,b,c,若a > b,c > 0,类似地,可以得到
ac>bc, .
综上可得不等式的基本性质2 :
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即,如果a > b,c > 0,那么 ac > bc , > .
例2 用“>”或“<”填空:
(1)已知a
解 (1)因为a
aπ
> .
>
<
例3 利用 >2,比较 与 的大小.
解 因为 >2,根据不等式的基本性质1得,
> 2-1,
即 >1.
又因为 >0,根据不等式的基本性质2得,
> .
1 已知3<π,用“>”或“<”填空:
(1)3+ π+; (2)1 π-2;
(3) ; (4) π.
<
<
<
<
2 已知a
(1)a+xy b+xy; (2)a-2x b-2x;
(3)5a 5b; (4) .
<
<
<
<
3 利用>6,比较 与 的大小.
1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b -10 a -10 .
<
>
因为 a>b,两边都乘3,
解:
由不等式基本性质2,得
3a > 3b.
已知 a>b,则3a 3b ;
>
2.用“>”或“<”填空:
同课章节目录
