3.2.2 不等式的基本性质3 课件(共39张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 3.2.2 不等式的基本性质3 课件(共39张PPT)2024-2025学年数学湘教版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 16:27:16 | ||
图片预览









文档简介
(共39张PPT)
3.2 不等式的基本性质
3.2.2 不等式的基本性质3
1.用不等号填空:
(1)6 4;
6 ÷ (-2) 4 ÷ (-2) .
(2)-2 -4;
-2 ÷ (-2) (-4) ÷ (-2).
>
<
>
<
2.在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b:已知每队人员均为3名,则哪队的平均得分高?用不等号填空:
a÷3 b÷3.
>
先用“>”或“<”填空:
4 3,-4 -3,
2( ≈ 1.414),- -1.
再观察结果,由此可猜测出什么结论?
显然 4 > 3,-4 < -3.
由于 ≈ 1.414,- ≈ -0.707,所以<2,->-1.
由此猜测:若a,b,c都是实数,且abc, > .
下面来说明上述猜测是真的.
已知a又c<0,于是 (a-b)c>0,
从而有 ac-bc>0,
因此 ac>bc.
又 < 0,同理可得 a· > b·,即
> .
若a > b,c > 0,类似地,可以得到
ac<bc, .
综上可得不等式的基本性质3:
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a > b,c < 0,那么 ac < bc , < .
例4 用“>”或“<”填空:
(1)已知a(2)已知a>b,则 - -.
解(1)因为a->-.
(2)因为a>b,两边都乘 -由不等式的基本性质3,得
- <-.
因为 a>b,两边都乘-1,
由不等式基本性质3,得
-a < -b.
(1)已知 a>b,则-a -b .
<
1.用“>”或“<”填空:
因为 a由不等式基本性质3,得
由不等式基本性质1,得
(2)已知 a>
因为 ,两边都加上2,
2.下面是某同学根据不等式的性质做的一道题:
在不等式 -4x+5>9的两边都减去5,得
-4x > 4
在不等式-4x> 4的两边都除以 -4,得
x > -1
请问他做对了吗?如果不对,请改正.
不对
x < -1
(1)如果a>b,那么ac>bc.
(2)如果 a > b,那么ac2 > bc2.
(3)如果ac2>bc2,那么a>b.
3.判断正误:
×
×
√
当c≤0时,不成立.
当 c = 0 时,不成立.
思考: 不等式的基本性质与等式的基本性质有什么相同点和不同点?
已知 x > 5,那么 5 < x吗
思考: 等式有对称性及传递性,那么不等式具有对称性和传递性吗
x > 5 5 < x
性质(对称性):如果 a > b,那么 b < a.
思考: 等式有对称性及传递性,那么不等式具有对称性和传递性吗
由8 < x,x < y,可以得到 8 < y吗
如:8 < 10,10 < 15 ,8 15.
<
性质(同向传递性):
如果 a > b,b > c,那么 a > c.
1.如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足
______________.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1.
a<-1
2.利用不等式的性质解下列不等式:
(1) x-7>26; (2) 3x < 2x+1;
(3) >50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
思路:
解 根据不等式的性质1,
不等式两边都加7,不等号的方向不变,
得 x-7+7﹥26+7,即x﹥33.
(1) x-7>26;
(2) 3x<2x+1;
根据_____________,
不等式两边都减去____,不等号的方向_____,得 .
3x-2x﹤2x+1-2x ,即 x﹤1
不等式性质1
2x
不变
为了使不等式 ﹥50中不等号的一边变为x,根据
不等式的性质2,不等式的两边都除以 ,不等号的
方向不变,得
x﹥75.
(3) >50;
为了使不等式-4x﹥3中的不等号的一边变为x,
根据______________,不等式两边都除以____,
不等号的方向______,得
x﹤- .
不等式的性质3
-4
改变
(4) -4x>3.
例5 把下列不等式化为 x<a 或 x>a 的形式:
(1)10x < 3x-7; (2)-(x+5)+1 < .
解 (1)根据不等式的基本性质1,得
10x-3x < 3x-7-3x,
合并同类项,得 7x<-7.
两边都除以7,根据不等式的基本性质2,得x<-1.
(2)两边都乘21,根据不等式的基本性质2,得
-(x+5)×21+1×21 < ×21,
即 -3(x+5)+21<7.
运用乘法对加法的分配律,得
-3x-15+21<7,
合并同类项,得
-3x+6<7.
根据不等式的基本性质1,得
-3x+6-6<7-6,
合并同类项,得
-3x<1.
两边都除以-3,根据不等式的基本性质3,得
x>-.
对于不等式10x<3x-7,
运用不等式的基本性质1,两边都减去3x,得7x<-7.
这种变形可看作是把不等式右边的项3x改变符号后移到左边.
10x < 3x-7,
10x-3x < -7.
对于不等式-3x+6<7,
运用不等式的基本性质1,两边都减去6,得-3x<1.
这种变形可看作是把不等式左边的项6改变符号后移到右边.
-3x+6 < 7,
-3x < 7-6.
像这样,把不等式一边的某一项改变符号后移到另一边的变形称为移项.
在例5(2)中,将原不等式的两边都乘各个分母的最小公倍数,从而把分母去掉,这种变形叫作去分母,
有时还需运用乘法对加法的分配律,把不等式中的括号去掉,这种变形叫作去括号.
1 已知3<π,用“>”或“<”填空:
(1)- -π; (2)- -;
(3) +1; (4) -+2.
>
>
>
<
2 把下列不等式化为xa的形式:
(1)5x+8>-2; (2)2x(3)-x+1<-; (4)3(x+4)<
1. 已知 a > b,用“>”或“<”填空:
(1)2a 2b ;
(2)-3a -3b ;
>
<
(3) .
2. 用” >“或” <“填空:
(1) 如果1-x>3,那么-x 3-1,得x -2;
(2) 如果x+2<3x+8,那么x-3x 8-2,即-2x 6,得x -3;
>
<
<
<
>
解:(1)根据不等式的基本性质1,
两边都加上2得:2x<2.
根据不等式的基本性质2,
两边除以2得:x<1;
2x-2 < 0
2x-2+2 < 0 + 2
2x < 2
2x ÷2 < 2 ÷2
x<1
解:(2) 根据不等式的基本性质1,
两边都加上 9-6x 得:-3x<9.
根据不等式的基本性质3,
两边都除以-3得:x>-3;
3x-9 < 6x
3x-9 + 9 -6x < 6x+ 9-6x
-3x < 9
-3x÷(-3 ) > 9÷(-3)
x >-3
解:(3) 根据不等式的基本性质1,
两边都加上2-x得:- x > -3.
根据不等式的基本性质3,
两边都除以- 得:x <18;
x <18
3.2 不等式的基本性质
3.2.2 不等式的基本性质3
1.用不等号填空:
(1)6 4;
6 ÷ (-2) 4 ÷ (-2) .
(2)-2 -4;
-2 ÷ (-2) (-4) ÷ (-2).
>
<
>
<
2.在某次知识抢答赛中,甲、乙两队的总得分分别为a,b,其中a>b:已知每队人员均为3名,则哪队的平均得分高?用不等号填空:
a÷3 b÷3.
>
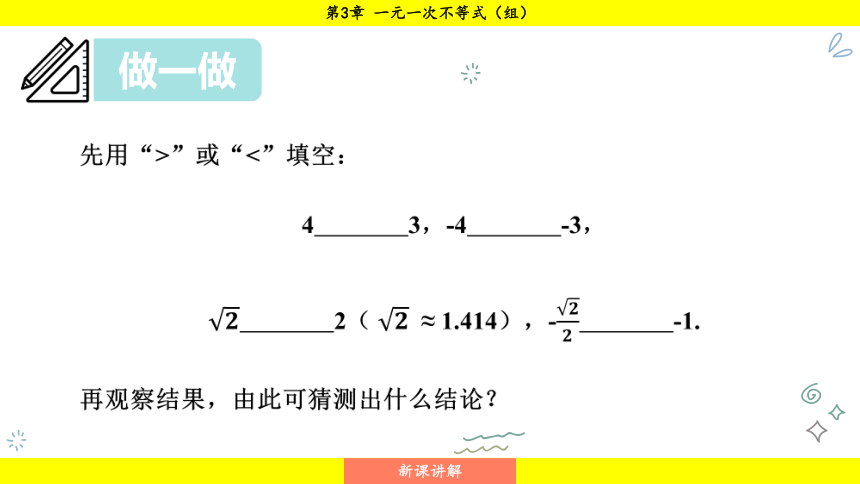
先用“>”或“<”填空:
4 3,-4 -3,
2( ≈ 1.414),- -1.
再观察结果,由此可猜测出什么结论?
显然 4 > 3,-4 < -3.
由于 ≈ 1.414,- ≈ -0.707,所以<2,->-1.
由此猜测:若a,b,c都是实数,且a
下面来说明上述猜测是真的.
已知a
从而有 ac-bc>0,
因此 ac>bc.
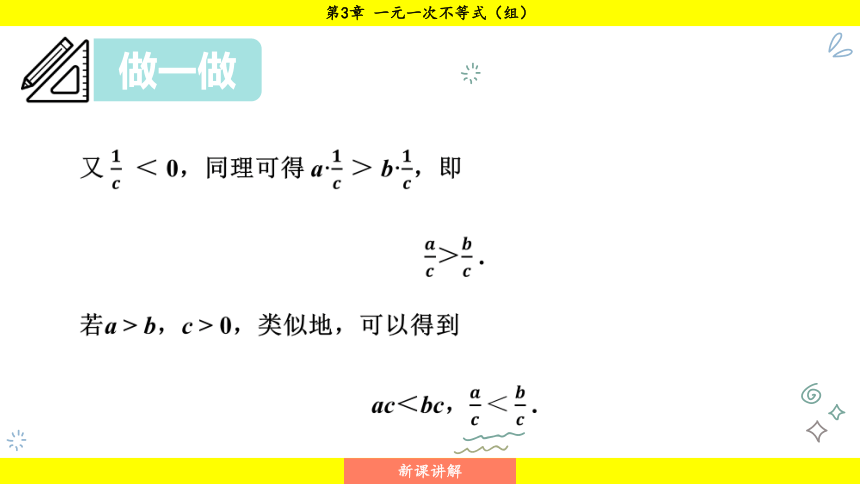
又 < 0,同理可得 a· > b·,即
> .
若a > b,c > 0,类似地,可以得到
ac<bc, .
综上可得不等式的基本性质3:
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即,如果a > b,c < 0,那么 ac < bc , < .
例4 用“>”或“<”填空:
(1)已知a
解(1)因为a
(2)因为a>b,两边都乘 -由不等式的基本性质3,得
- <-.
因为 a>b,两边都乘-1,
由不等式基本性质3,得
-a < -b.
(1)已知 a>b,则-a -b .
<
1.用“>”或“<”填空:
因为 a
由不等式基本性质1,得
(2)已知 a
因为 ,两边都加上2,
2.下面是某同学根据不等式的性质做的一道题:
在不等式 -4x+5>9的两边都减去5,得
-4x > 4
在不等式-4x> 4的两边都除以 -4,得
x > -1
请问他做对了吗?如果不对,请改正.
不对
x < -1
(1)如果a>b,那么ac>bc.
(2)如果 a > b,那么ac2 > bc2.
(3)如果ac2>bc2,那么a>b.
3.判断正误:
×
×
√
当c≤0时,不成立.
当 c = 0 时,不成立.
思考: 不等式的基本性质与等式的基本性质有什么相同点和不同点?
已知 x > 5,那么 5 < x吗
思考: 等式有对称性及传递性,那么不等式具有对称性和传递性吗
x > 5 5 < x
性质(对称性):如果 a > b,那么 b < a.
思考: 等式有对称性及传递性,那么不等式具有对称性和传递性吗
由8 < x,x < y,可以得到 8 < y吗
如:8 < 10,10 < 15 ,8 15.
<
性质(同向传递性):
如果 a > b,b > c,那么 a > c.
1.如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足
______________.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1.
a<-1
2.利用不等式的性质解下列不等式:
(1) x-7>26; (2) 3x < 2x+1;
(3) >50; (4) -4x>3.
解未知数为x的不等式
化为x>a或x﹤a的形式
目标
方法:不等式基本性质1~3
思路:
解 根据不等式的性质1,
不等式两边都加7,不等号的方向不变,
得 x-7+7﹥26+7,即x﹥33.
(1) x-7>26;
(2) 3x<2x+1;
根据_____________,
不等式两边都减去____,不等号的方向_____,得 .
3x-2x﹤2x+1-2x ,即 x﹤1
不等式性质1
2x
不变
为了使不等式 ﹥50中不等号的一边变为x,根据
不等式的性质2,不等式的两边都除以 ,不等号的
方向不变,得
x﹥75.
(3) >50;
为了使不等式-4x﹥3中的不等号的一边变为x,
根据______________,不等式两边都除以____,
不等号的方向______,得
x﹤- .
不等式的性质3
-4
改变
(4) -4x>3.
例5 把下列不等式化为 x<a 或 x>a 的形式:
(1)10x < 3x-7; (2)-(x+5)+1 < .
解 (1)根据不等式的基本性质1,得
10x-3x < 3x-7-3x,
合并同类项,得 7x<-7.
两边都除以7,根据不等式的基本性质2,得x<-1.
(2)两边都乘21,根据不等式的基本性质2,得
-(x+5)×21+1×21 < ×21,
即 -3(x+5)+21<7.
运用乘法对加法的分配律,得
-3x-15+21<7,
合并同类项,得
-3x+6<7.
根据不等式的基本性质1,得
-3x+6-6<7-6,
合并同类项,得
-3x<1.
两边都除以-3,根据不等式的基本性质3,得
x>-.
对于不等式10x<3x-7,
运用不等式的基本性质1,两边都减去3x,得7x<-7.
这种变形可看作是把不等式右边的项3x改变符号后移到左边.
10x < 3x-7,
10x-3x < -7.
对于不等式-3x+6<7,
运用不等式的基本性质1,两边都减去6,得-3x<1.
这种变形可看作是把不等式左边的项6改变符号后移到右边.
-3x+6 < 7,
-3x < 7-6.
像这样,把不等式一边的某一项改变符号后移到另一边的变形称为移项.
在例5(2)中,将原不等式的两边都乘各个分母的最小公倍数,从而把分母去掉,这种变形叫作去分母,
有时还需运用乘法对加法的分配律,把不等式中的括号去掉,这种变形叫作去括号.
1 已知3<π,用“>”或“<”填空:
(1)- -π; (2)- -;
(3) +1; (4) -+2.
>
>
>
<
2 把下列不等式化为x
(1)5x+8>-2; (2)2x
1. 已知 a > b,用“>”或“<”填空:
(1)2a 2b ;
(2)-3a -3b ;
>
<
(3) .
2. 用” >“或” <“填空:
(1) 如果1-x>3,那么-x 3-1,得x -2;
(2) 如果x+2<3x+8,那么x-3x 8-2,即-2x 6,得x -3;
>
<
<
<
>
解:(1)根据不等式的基本性质1,
两边都加上2得:2x<2.
根据不等式的基本性质2,
两边除以2得:x<1;
2x-2 < 0
2x-2+2 < 0 + 2
2x < 2
2x ÷2 < 2 ÷2
x<1
解:(2) 根据不等式的基本性质1,
两边都加上 9-6x 得:-3x<9.
根据不等式的基本性质3,
两边都除以-3得:x>-3;
3x-9 < 6x
3x-9 + 9 -6x < 6x+ 9-6x
-3x < 9
-3x÷(-3 ) > 9÷(-3)
x >-3
解:(3) 根据不等式的基本性质1,
两边都加上2-x得:- x > -3.
根据不等式的基本性质3,
两边都除以- 得:x <18;
x <18
同课章节目录
