4.1.2 相交直线所成的角 课件(共57张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 4.1.2 相交直线所成的角 课件(共57张PPT)2024-2025学年数学湘教版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 16:29:47 | ||
图片预览







文档简介
(共57张PPT)
4.1 平面内两条直线的位置关系
4.1.2 相交直线所成的角
1.在同一平面内,不相交的两条直线叫做平行线.
2.过直线外一点有且只有一条直线与这条直线平行.
3.平行于同一条直线的两条直线平行.
你发现了什么?
直线与直线相交于一点,并形成了四个角.
如图,随着剪刀的两个把手之间的角度变化,
剪刀刃之间的角也相应变化.
如果把剪刀的构造看作两条相交的直线,
这就关系到两条相交直线所成的角的问题.
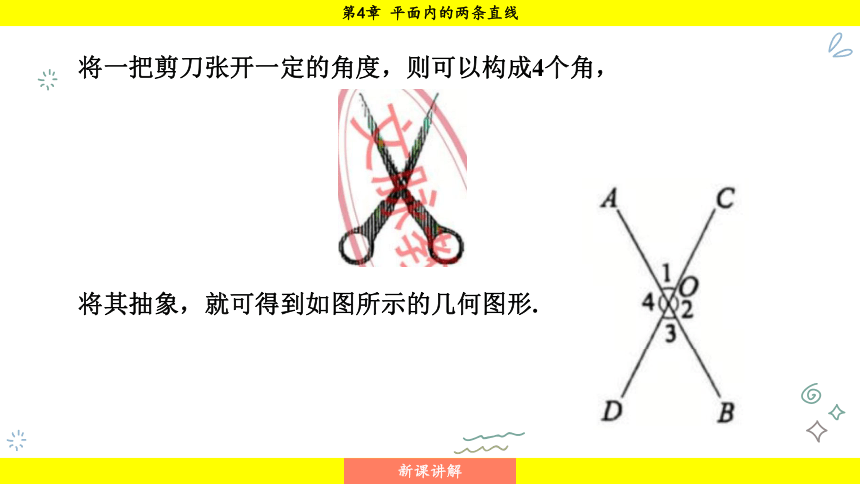
将一把剪刀张开一定的角度,则可以构成4个角,
将其抽象,就可得到如图所示的几何图形.
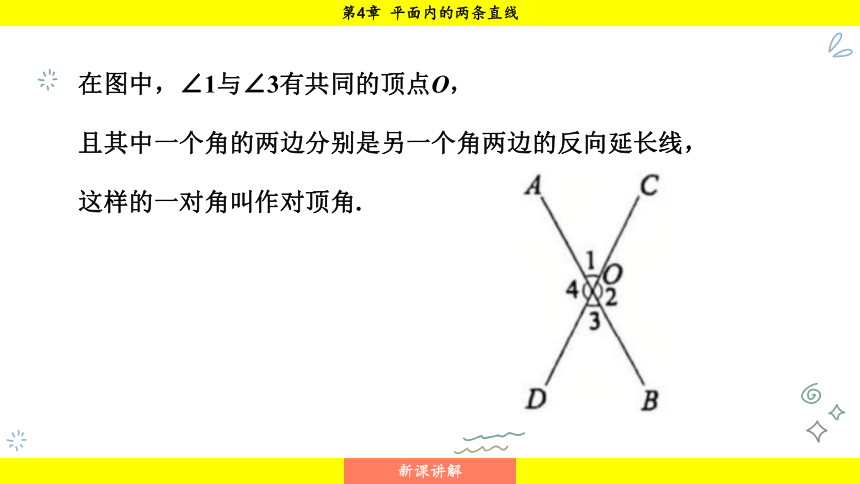
在图中,∠1与∠3有共同的顶点O,
且其中一个角的两边分别是另一个角两边的反向延长线,
这样的一对角叫作对顶角.
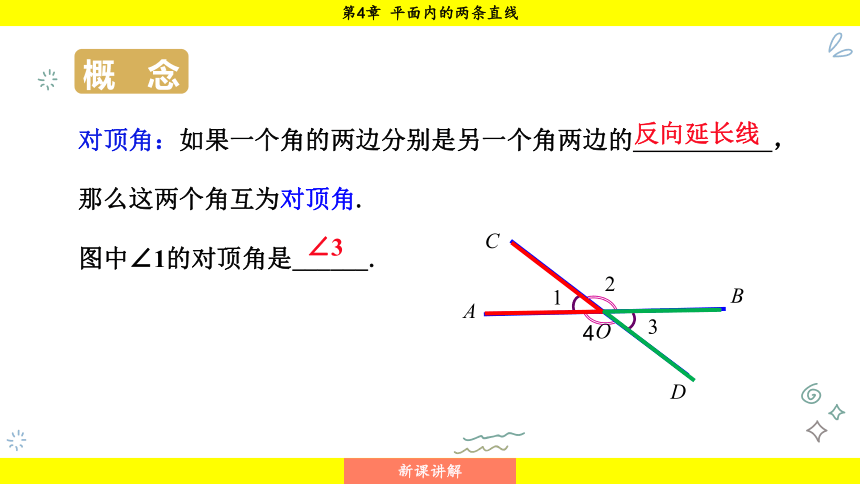
对顶角:如果一个角的两边分别是另一个角两边的 ,
那么这两个角互为对顶角.
图中∠1的对顶角是______.
概念
1
2
3
4
A
B
C
D
O
反向延长线
∠3
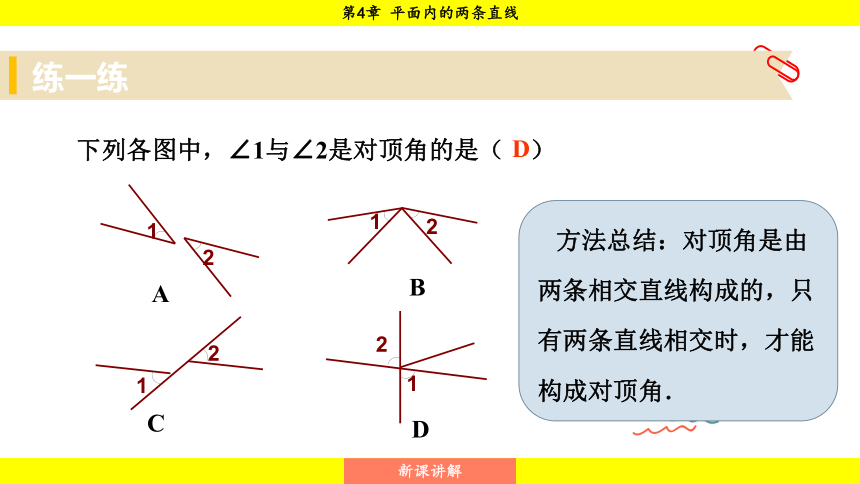
下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
方法总结:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.
比较图中∠1与∠3的大小,它们的大小之间有怎样的关系?
在上学期我们已经知道互为补角的两个角和为180°,
因而互为邻补角的两个角和为180°.
猜想:对顶角相等
你能利用有关知识来验证∠1 与∠3的大小关系吗?
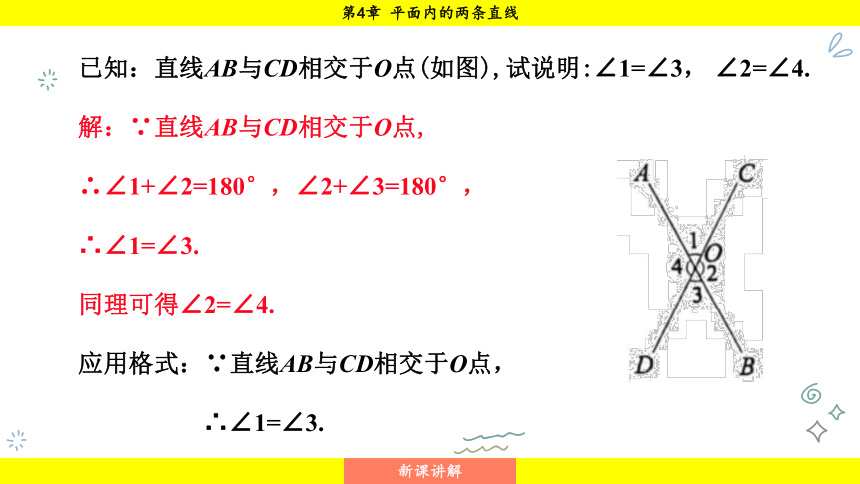
已知:直线AB与CD相交于O点(如图),试说明:∠1=∠3, ∠2=∠4.
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°,∠2+∠3=180°,
∴∠1=∠3.
同理可得∠2=∠4.
应用格式:∵直线AB与CD相交于O点,
∴∠1=∠3.
从图中可以看出,∠1与∠ 2互补, ∠ 3与∠ 2也互补,
即∠ 1与∠ 3都是∠ 2的补角.
由“同角的补角相等”,可以得出∠ 1= ∠ 3.
类似地, ∠ 2= ∠ 4.
综上可得对顶角的性质:对顶角相等.
想一想:
图中是对顶角量角器,你能说出用它测量角的原理吗?
对顶角相等
1.如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
∴∠2=180°-∠1=140°,
∵∠3=∠1,
∠1=40°,
∴∠3=40°,
解:
∴∠4=∠2=140°.
掌握对顶角的性质是解题的关键!
方法
变式训练:①若∠1+∠3= 60 ,则∠1,∠2,∠3,∠4各个角的度数分别为________________________
②若∠2是∠1的 3倍,则∠1,∠2,∠3,∠4各个角的度数分别为________________________
③若 1: 2 = 2: 7 ,则∠1,∠2,∠3,∠4各个角的度数分别为________________________
30 、150 、30 、150
45 、 135 、 45 、 135
40 、140 、40 、140
2.如图,直线AB、CD、EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:因为∠1=40°,∠BOC=110°(已知),
所以∠BOF=∠BOC-∠1
=110°-40°=70°.
因为∠BOF=∠2(对顶角相等), 所以∠2=70°(等量代换).
注意:隐含条件“对顶角相等”.
3.如图,直线AB、CD、EF相交,若∠1 +∠5=180°,找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵ ∠1= ∠3(对顶角相等)
1
2
3
4
5
6
8
7
∠5+∠8=180 °且∠1 +∠5=180°
∴∠8= ∠1
∵ ∠8= ∠6(对顶角相等)
∴∠6= ∠1.
4.如图,直线AB、CD、EF、MN相交,若∠2=∠5,
找出图中与∠2 互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ ∠1+∠2=180°,∠2+∠3= 180°,
∴∠2的补角有∠1和∠3,
∵ ∠5+∠8=180°,∠5+∠6=180 °且∠2=∠5,
∴∠2的补角有∠6和∠8.
设直线AB,CD都与第三条直线MN相交(有时也说直线AB,CD被第三条直线MN所截),则可以构成8个角,如图所示.
(1) ∠ 1和∠ 5的位置有什么关系?
(2) ∠ 3和∠ 5, ∠ 3和∠ 6的位置分别
有什么关系?
简称“三线八角”
可以发现,在图中,
∠ 1和∠ 5分别在直线AB,CD的同一方(上方),
并且都在直线MN的同侧(右侧).
具有∠ 1和∠ 5这种位置关系的一对角叫作同位角.
下列图形中,∠1和∠2是同位角的是( )
A.(1),(2) B.(3),(4)
C.(1),(2),(3) D.(2),(3) ,(3)
A
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
图形特征:在形如字母“F”的图形中有同位角.
1
2
1
2
1
2
1
2
变式图形:图中的∠1与∠2都是同位角.
∠ 3和∠ 5都在直线AB,CD之间,
并且分别在直线MN的两侧
( ∠ 3在直线MN左侧, ∠ 5在直线MN右侧).
具有∠ 3和∠ 5这种位置关系的一对角叫作内错角.
如图,与∠1是内错角的是( )
A. ∠2 B. ∠3
C. ∠4 D. ∠5
1
3
2
4
5
B
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
变式图形:图中的∠1与∠2都是内错角.
∠ 3和∠ 6都在直线AB,CD之间,
但它们在直线MN的同一旁(左侧).
具有∠ 3和∠ 6这种位置关系的一对角叫作同旁内角.
1
1
A
B
C
D
1
2
2
2
1
2
A
下列图形中,∠1和∠2是同旁内角的是( )
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
图中还有其他的同位角、内错角和同旁内角吗?如有,将它们分别找出来,并将你的结果与同学的结果进行比较.
同位角:∠2和∠6;∠3和∠7;∠4和∠8.
内错角:∠4和∠6.
同旁内角 :∠4和∠5.
例1 如图,直线EF与直线AB,CD分别相交,构成8个角.
指出图中所有的对顶角、同位角、内错角和同旁内角.
解 由图可知,其中对顶角有:
∠ 1和∠ 3, ∠ 2和∠ 4,
∠ 5和∠ 7, ∠ 6和∠ 8.
同位角有: ∠ 2和∠ 5, ∠ 1和∠ 8,
∠ 3和∠ 6,∠ 4和∠ 7.
内错角有: ∠ 1和∠ 6, ∠ 4和∠ 5.
同旁内角有: ∠ 1和∠ 5, ∠ 4和∠ 6.
例2 如图,直线AB,CD被直线MN所截,
同位角∠ 1与∠ 2相等,那么内错角∠ 2与∠ 3相等吗?
解 因为∠ 1= ∠ 3(对顶角相等),
∠ 1= ∠ 2(已知),
所以∠ 2= ∠ 3(等量代换).
由上可知:
两条直线被第三条直线所截,
如果有一对同位角相等,则内错角相等.
1.如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
E
D
C
B
A
8
7
6
5
4
3
2
1
变式:∠A与∠8是哪两条直线被哪条直线所截的角
它们是什么关系的角
∠A与∠5呢
∠A与∠6呢
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
同位角
同位角
同位角
2.识别哪些角是同位角、内错角、同旁内角.
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
内错角
同旁内角
2.识别哪些角是同位角、内错角、同旁内角.
3.如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,
∠1和∠3同旁内角,
∠1和∠4是同旁内角.
温馨提示:解题之前要明确哪两条直线被哪条直线所截.
(2)如果∠1=∠4,那∠1与∠2相等吗?∠1与∠3互补吗? 为什么?
解:(2)如果∠1=∠4,
由对顶角相等,得∠2=∠4,那么∠1=∠2.
因为∠3和∠4互补,即∠4+∠3=180°,
又因为∠1=∠4,所以∠4+∠3=180°,
即∠1与∠3互补.
4
3
2
1
F
E
D
C
B
A
截线 被截线 结构特征 相同点 公共特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
都在截线同侧
都在被截线之间
这三类角都没有公共顶点
1 请举出生活中对顶角的例子.
2 如图,工人师傅用对顶角量角器量工件a,b边所夹的角,其中∠ 1的度数可以从仪器上读出.
试说明∠ 1的大小就是a,b边所夹角的大小的理由.
3 如图,直线a,b被直线c所截,
试找出图中所有的对顶角、同位角、内错角和同旁内角.
若∠ 1= ∠ 5=107°,求其他角的度数.
(
)
1
2
(
)
1
2
(
)
2
1
不是
是
不是
1.下列各图中, ∠1 ,∠2是对顶角吗?
2.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC, ∠BOE的补角;
解 ∠AOC的补角是∠AOD和∠COB;
∠BOE的补角是∠EOA和∠BOF.
A
E
D
B
F
C
O
(2)写出∠DOA, ∠EOC的对顶角;
∠DOA的对顶角是∠COB;
∠EOC的对顶角是∠DOF.
(3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
∠BOD=∠AOC= 50°;∠COB=180°-∠AOC=130°.
A
E
D
B
F
C
O
C
A
D
B
C
E
3.如图,∠DAB和∠ABC的位置关系是( )
A.同位角
B.同旁内角
C.内错角
D.以上结论都不对
4.如图,∠1和∠2不能构成同位角的图形是( )
D
5. (1)如图1,若ED,BF被AB所截,则∠1与____是同位角.
(2)如图2,若ED,BC被AF所截,则∠3与___ 是内错角.
∠2
∠4
图1
图2
(3)如图3,∠1与∠3是AB和AF被_____所截构成的 __ 角;
(4)如图4,∠2与∠4是 和 被BC所截构成的______角.
DE
内错
AB
AF
同位
图3
图4
A
B
C
D
E
O
解:∵OA平分∠EOC,
∴∠AOC= ∠EOC=35°,
∴∠BOD=∠AOC=35°.
6.如图,直线AB,CD相交于点O, ∠EOC=70°,OA平分∠EOC,
求∠BOD的度数.
7.学校与游乐场所在的角
形成一对( )角;
学校与超市所在的角
形成一对( )角;
学校与飞机场所在的角
形成一对( )角.
同位
同旁内
内错
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
相交直线所成的角
对顶角
对顶角相等
三线八角
同位角、内错角、同旁内角
4.1 平面内两条直线的位置关系
4.1.2 相交直线所成的角
1.在同一平面内,不相交的两条直线叫做平行线.
2.过直线外一点有且只有一条直线与这条直线平行.
3.平行于同一条直线的两条直线平行.
你发现了什么?
直线与直线相交于一点,并形成了四个角.
如图,随着剪刀的两个把手之间的角度变化,
剪刀刃之间的角也相应变化.
如果把剪刀的构造看作两条相交的直线,
这就关系到两条相交直线所成的角的问题.
将一把剪刀张开一定的角度,则可以构成4个角,
将其抽象,就可得到如图所示的几何图形.
在图中,∠1与∠3有共同的顶点O,
且其中一个角的两边分别是另一个角两边的反向延长线,
这样的一对角叫作对顶角.
对顶角:如果一个角的两边分别是另一个角两边的 ,
那么这两个角互为对顶角.
图中∠1的对顶角是______.
概念
1
2
3
4
A
B
C
D
O
反向延长线
∠3
下列各图中,∠1与∠2是对顶角的是( )
1
2
C
1
2
D
D
1
2
A
1
2
B
方法总结:对顶角是由两条相交直线构成的,只有两条直线相交时,才能构成对顶角.
比较图中∠1与∠3的大小,它们的大小之间有怎样的关系?
在上学期我们已经知道互为补角的两个角和为180°,
因而互为邻补角的两个角和为180°.
猜想:对顶角相等
你能利用有关知识来验证∠1 与∠3的大小关系吗?
已知:直线AB与CD相交于O点(如图),试说明:∠1=∠3, ∠2=∠4.
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°,∠2+∠3=180°,
∴∠1=∠3.
同理可得∠2=∠4.
应用格式:∵直线AB与CD相交于O点,
∴∠1=∠3.
从图中可以看出,∠1与∠ 2互补, ∠ 3与∠ 2也互补,
即∠ 1与∠ 3都是∠ 2的补角.
由“同角的补角相等”,可以得出∠ 1= ∠ 3.
类似地, ∠ 2= ∠ 4.
综上可得对顶角的性质:对顶角相等.
想一想:
图中是对顶角量角器,你能说出用它测量角的原理吗?
对顶角相等
1.如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.
∴∠2=180°-∠1=140°,
∵∠3=∠1,
∠1=40°,
∴∠3=40°,
解:
∴∠4=∠2=140°.
掌握对顶角的性质是解题的关键!
方法
变式训练:①若∠1+∠3= 60 ,则∠1,∠2,∠3,∠4各个角的度数分别为________________________
②若∠2是∠1的 3倍,则∠1,∠2,∠3,∠4各个角的度数分别为________________________
③若 1: 2 = 2: 7 ,则∠1,∠2,∠3,∠4各个角的度数分别为________________________
30 、150 、30 、150
45 、 135 、 45 、 135
40 、140 、40 、140
2.如图,直线AB、CD、EF相交于点O,∠1=40°,∠BOC=110°,求∠2的度数.
解:因为∠1=40°,∠BOC=110°(已知),
所以∠BOF=∠BOC-∠1
=110°-40°=70°.
因为∠BOF=∠2(对顶角相等), 所以∠2=70°(等量代换).
注意:隐含条件“对顶角相等”.
3.如图,直线AB、CD、EF相交,若∠1 +∠5=180°,找出图中与∠1 相等的角.
D
B
E
O
A
C
F
解:∵ ∠1= ∠3(对顶角相等)
1
2
3
4
5
6
8
7
∠5+∠8=180 °且∠1 +∠5=180°
∴∠8= ∠1
∵ ∠8= ∠6(对顶角相等)
∴∠6= ∠1.
4.如图,直线AB、CD、EF、MN相交,若∠2=∠5,
找出图中与∠2 互补的角.
F
N
C
E
A
B
D
M
1
2
3
4
5
8
6
7
解:∵ ∠1+∠2=180°,∠2+∠3= 180°,
∴∠2的补角有∠1和∠3,
∵ ∠5+∠8=180°,∠5+∠6=180 °且∠2=∠5,
∴∠2的补角有∠6和∠8.
设直线AB,CD都与第三条直线MN相交(有时也说直线AB,CD被第三条直线MN所截),则可以构成8个角,如图所示.
(1) ∠ 1和∠ 5的位置有什么关系?
(2) ∠ 3和∠ 5, ∠ 3和∠ 6的位置分别
有什么关系?
简称“三线八角”
可以发现,在图中,
∠ 1和∠ 5分别在直线AB,CD的同一方(上方),
并且都在直线MN的同侧(右侧).
具有∠ 1和∠ 5这种位置关系的一对角叫作同位角.
下列图形中,∠1和∠2是同位角的是( )
A.(1),(2) B.(3),(4)
C.(1),(2),(3) D.(2),(3) ,(3)
A
1
2
1
2
1
2
1
2
(1) (2) (3) (4)
图形特征:在形如字母“F”的图形中有同位角.
1
2
1
2
1
2
1
2
变式图形:图中的∠1与∠2都是同位角.
∠ 3和∠ 5都在直线AB,CD之间,
并且分别在直线MN的两侧
( ∠ 3在直线MN左侧, ∠ 5在直线MN右侧).
具有∠ 3和∠ 5这种位置关系的一对角叫作内错角.
如图,与∠1是内错角的是( )
A. ∠2 B. ∠3
C. ∠4 D. ∠5
1
3
2
4
5
B
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
变式图形:图中的∠1与∠2都是内错角.
∠ 3和∠ 6都在直线AB,CD之间,
但它们在直线MN的同一旁(左侧).
具有∠ 3和∠ 6这种位置关系的一对角叫作同旁内角.
1
1
A
B
C
D
1
2
2
2
1
2
A
下列图形中,∠1和∠2是同旁内角的是( )
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
图中还有其他的同位角、内错角和同旁内角吗?如有,将它们分别找出来,并将你的结果与同学的结果进行比较.
同位角:∠2和∠6;∠3和∠7;∠4和∠8.
内错角:∠4和∠6.
同旁内角 :∠4和∠5.
例1 如图,直线EF与直线AB,CD分别相交,构成8个角.
指出图中所有的对顶角、同位角、内错角和同旁内角.
解 由图可知,其中对顶角有:
∠ 1和∠ 3, ∠ 2和∠ 4,
∠ 5和∠ 7, ∠ 6和∠ 8.
同位角有: ∠ 2和∠ 5, ∠ 1和∠ 8,
∠ 3和∠ 6,∠ 4和∠ 7.
内错角有: ∠ 1和∠ 6, ∠ 4和∠ 5.
同旁内角有: ∠ 1和∠ 5, ∠ 4和∠ 6.
例2 如图,直线AB,CD被直线MN所截,
同位角∠ 1与∠ 2相等,那么内错角∠ 2与∠ 3相等吗?
解 因为∠ 1= ∠ 3(对顶角相等),
∠ 1= ∠ 2(已知),
所以∠ 2= ∠ 3(等量代换).
由上可知:
两条直线被第三条直线所截,
如果有一对同位角相等,则内错角相等.
1.如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
解:两条直线是AB,AC,截线是DE,
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
E
D
C
B
A
8
7
6
5
4
3
2
1
变式:∠A与∠8是哪两条直线被哪条直线所截的角
它们是什么关系的角
∠A与∠5呢
∠A与∠6呢
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
同位角
同位角
同位角
2.识别哪些角是同位角、内错角、同旁内角.
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
内错角
同旁内角
2.识别哪些角是同位角、内错角、同旁内角.
3.如图,直线DE,BC被直线AB所截.
(1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,
∠1和∠3同旁内角,
∠1和∠4是同旁内角.
温馨提示:解题之前要明确哪两条直线被哪条直线所截.
(2)如果∠1=∠4,那∠1与∠2相等吗?∠1与∠3互补吗? 为什么?
解:(2)如果∠1=∠4,
由对顶角相等,得∠2=∠4,那么∠1=∠2.
因为∠3和∠4互补,即∠4+∠3=180°,
又因为∠1=∠4,所以∠4+∠3=180°,
即∠1与∠3互补.
4
3
2
1
F
E
D
C
B
A
截线 被截线 结构特征 相同点 公共特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
都在截线同侧
都在被截线之间
这三类角都没有公共顶点
1 请举出生活中对顶角的例子.
2 如图,工人师傅用对顶角量角器量工件a,b边所夹的角,其中∠ 1的度数可以从仪器上读出.
试说明∠ 1的大小就是a,b边所夹角的大小的理由.
3 如图,直线a,b被直线c所截,
试找出图中所有的对顶角、同位角、内错角和同旁内角.
若∠ 1= ∠ 5=107°,求其他角的度数.
(
)
1
2
(
)
1
2
(
)
2
1
不是
是
不是
1.下列各图中, ∠1 ,∠2是对顶角吗?
2.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC, ∠BOE的补角;
解 ∠AOC的补角是∠AOD和∠COB;
∠BOE的补角是∠EOA和∠BOF.
A
E
D
B
F
C
O
(2)写出∠DOA, ∠EOC的对顶角;
∠DOA的对顶角是∠COB;
∠EOC的对顶角是∠DOF.
(3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
∠BOD=∠AOC= 50°;∠COB=180°-∠AOC=130°.
A
E
D
B
F
C
O
C
A
D
B
C
E
3.如图,∠DAB和∠ABC的位置关系是( )
A.同位角
B.同旁内角
C.内错角
D.以上结论都不对
4.如图,∠1和∠2不能构成同位角的图形是( )
D
5. (1)如图1,若ED,BF被AB所截,则∠1与____是同位角.
(2)如图2,若ED,BC被AF所截,则∠3与___ 是内错角.
∠2
∠4
图1
图2
(3)如图3,∠1与∠3是AB和AF被_____所截构成的 __ 角;
(4)如图4,∠2与∠4是 和 被BC所截构成的______角.
DE
内错
AB
AF
同位
图3
图4
A
B
C
D
E
O
解:∵OA平分∠EOC,
∴∠AOC= ∠EOC=35°,
∴∠BOD=∠AOC=35°.
6.如图,直线AB,CD相交于点O, ∠EOC=70°,OA平分∠EOC,
求∠BOD的度数.
7.学校与游乐场所在的角
形成一对( )角;
学校与超市所在的角
形成一对( )角;
学校与飞机场所在的角
形成一对( )角.
同位
同旁内
内错
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
相交直线所成的角
对顶角
对顶角相等
三线八角
同位角、内错角、同旁内角
同课章节目录
