4.3 平行线的性质 课件(共56张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 4.3 平行线的性质 课件(共56张PPT)2024-2025学年数学湘教版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 16:31:19 | ||
图片预览





文档简介
(共56张PPT)
4.3 平行线的性质
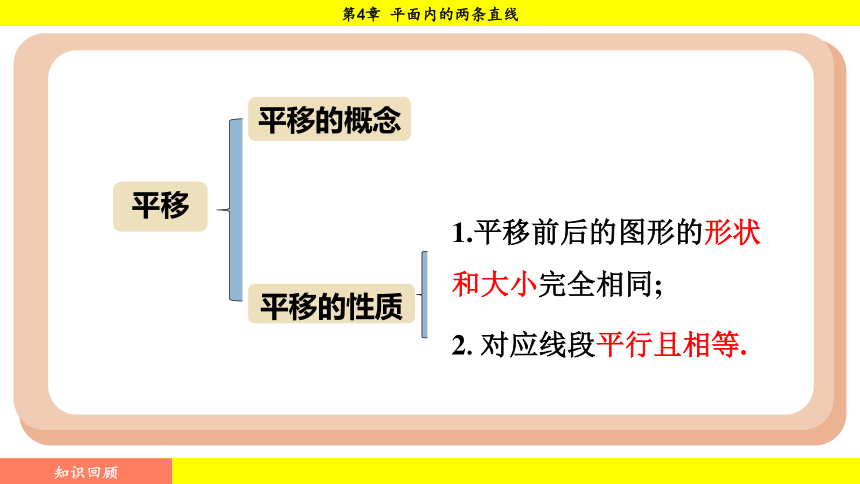
1.平移前后的图形的形状和大小完全相同;
2.对应线段平行且相等.
平移的概念
平移的性质
平移
问题1 同一平面内两条直线的位置关系有哪几种?
问题2 直线平行的定义是什么?
问题3 你学了平行线的哪些内容?
相交(包括垂直)、重合和平行.
在同一平面内,不相交的两条直线平行.
平行于同一条直线的两条直线平行.
过直线外一点有且只有一条直线与这条直线平行.
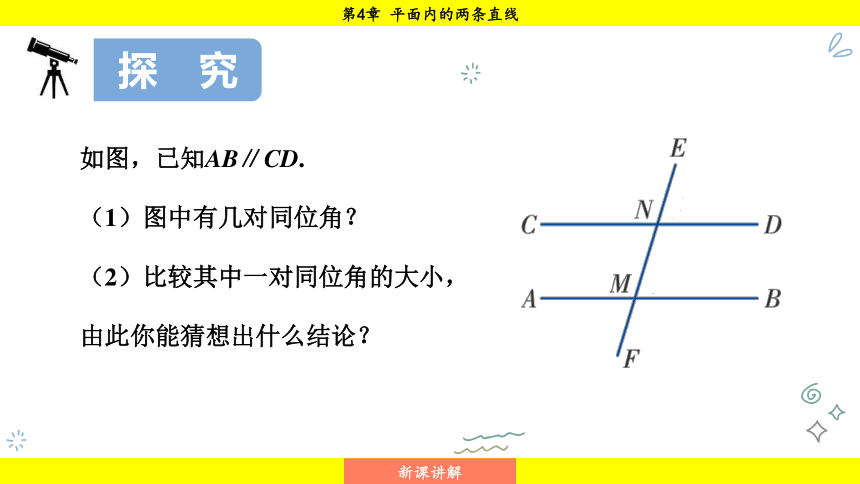
如图,已知AB∥CD.
(1)图中有几对同位角?
(2)比较其中一对同位角的大小,
由此你能猜想出什么结论?
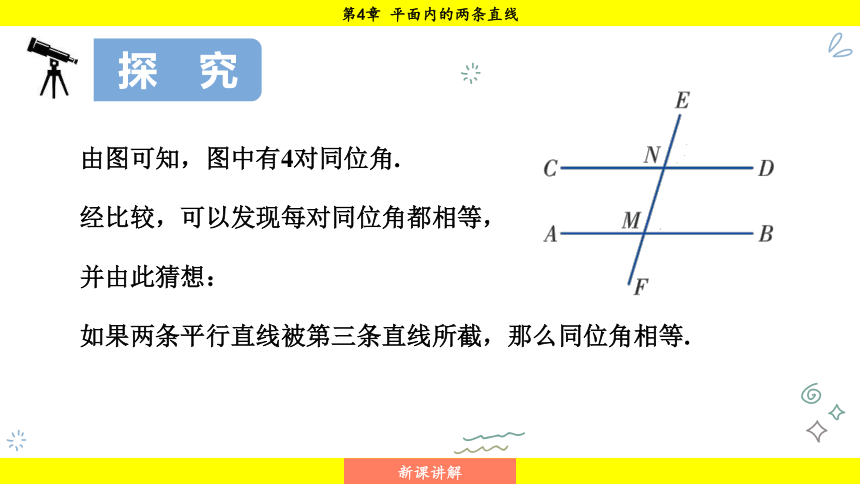
由图可知,图中有4对同位角.
经比较,可以发现每对同位角都相等,
并由此猜想:
如果两条平行直线被第三条直线所截,那么同位角相等.
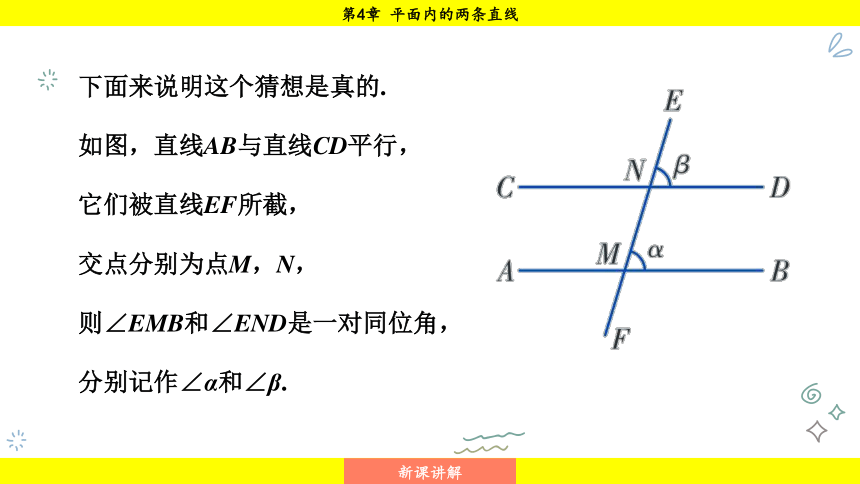
下面来说明这个猜想是真的.
如图,直线AB与直线CD平行,
它们被直线EF所截,
交点分别为点M,N,
则∠EMB和∠END是一对同位角,
分别记作∠α和∠β.
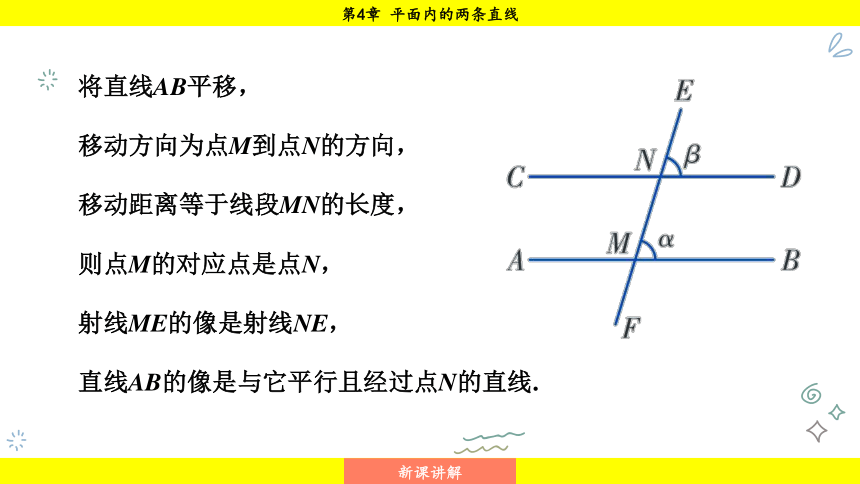
将直线AB平移,
移动方向为点M到点N的方向,
移动距离等于线段MN的长度,
则点M的对应点是点N,
射线ME的像是射线NE,
直线AB的像是与它平行且经过点N的直线.
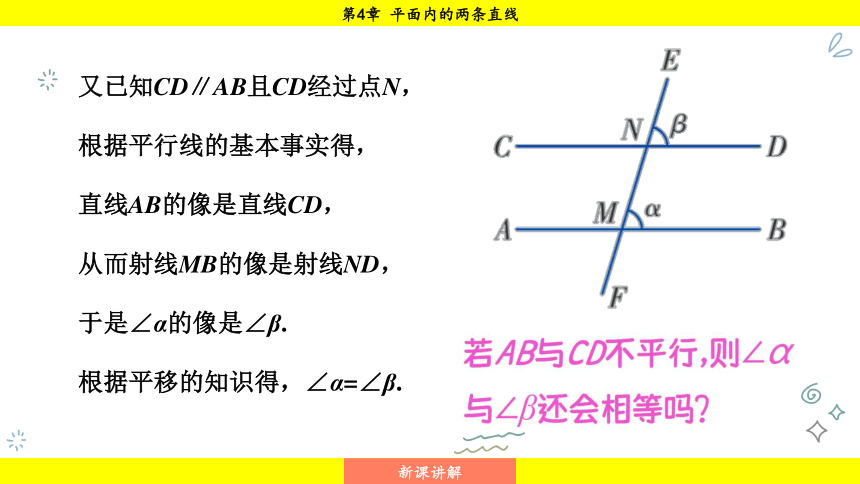
又已知CD∥AB且CD经过点N,
根据平行线的基本事实得,
直线AB的像是直线CD,
从而射线MB的像是射线ND,
于是∠α的像是∠β.
根据平移的知识得,∠α=∠β.
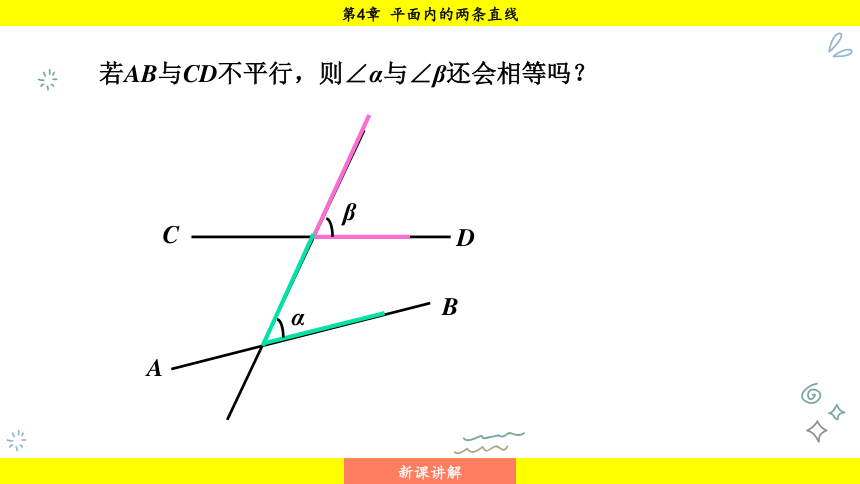
若AB与CD不平行,则∠α与∠β还会相等吗?
A
B
C
D
α
β
由此可得平行线的性质1:
两条平行直线被第三条
直线所截,同位角相等.
通常简单说成:
两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他测出∠A的度数吗?
D
C
E
F
A
A
G
G
1
2
两条平行直线被第三条直线所截,一对内错角的大小有什么关系?
之前的学习中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”.
类似的,已知两直线平行,同位角相等, 那么能否推出内错角之间的数量关系?
如图,两条平行直线AB,CD被直线EF所截, ∠ 1与∠ 2是内错角.
因为AB∥CD,
所以∠ 1= ∠ 4(两直线平行,同位角相等).
又因为∠ 2= ∠ 4(对顶角相等),
所以∠ 1= ∠ 2(等量代换).
A
B
C
D
E
F
由此可得平行线的性质2:
两条平行直线被第三条
直线所截,内错角相等.
通常简单说成:
两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
如图,AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?
B
D
C
E
A
解:过点E 作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
F
B
D
C
E
A
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB.
F
A
B
C
D
E
当左边有两个角,右边有一个角时:
∠A+∠C= ∠E
变式:如图,AB∥CD, 则:
如图,AB∥CD, 则:
当左边有两个角,右边有两个角时:
∠A+∠F= ∠E +∠D
C
A
B
D
E
F
如图,AB∥CD, 则:
当左边有三个角,右边有两个角时:
∠A+∠F1 +∠C =∠ E1+∠E2
E1
C
A
B
D
E2
F1
如图,AB∥CD,若左边有n个角,右边有m个角;你能找到规律吗?
当左边有n个角,右边有m个角时:
∠A+∠F1 + ∠ F2 +…+ ∠Fn= ∠E1 +∠E2 +…+ ∠Em+ ∠D
C
A
B
D
E1
F1
E2
Em
F2
Fn
两条平行直线被第三条直线所截,
一对同旁内角有什么关系?
为什么?
如图, ∠ 1与∠ 3是同旁内角.
因为AB//CD,
所以∠ 1= ∠ 4(两直线平行,同位角相等).
又因为∠ 3+ ∠ 4=180°,
所以∠ 1+ ∠ 3=180°(等量代换).
A
B
C
D
E
F
由此可得平行线的性质3:
两条平行直线被第三条
直线所截,同旁内角互补.
通常简单说成:
两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
∵a∥b(已知)
应用格式:
1.如图,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
A
B
C
D
解:因为梯形上、下底互相平行,所以
∠A与∠D互补, ∠B与∠C互补.
于是∠D=180 °-∠A=180°-100°=80°.
∠C= 180 °-∠B=180°-115°=65°.
解:过点E 作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD.
∴EF//CD.
F
2.如图,AB//CD,探索∠B、∠D与∠DEB的大小关系 .
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
F
变式:如图所示,AB∥CD,则 :
C
A
B
D
E
当有一个拐点时:
∠A+∠E+∠C= 360°
如图所示,AB∥CD,则 :
A
C
D
B
E2
E1
当有两个拐点时:
∠A+∠ E1 + ∠ E2 +∠C = 540°
如图所示,AB∥CD,则 :
当有三个拐点时:
∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
A
B
C
D
E1
E2
E3
如图所示,AB∥CD,若有n个拐点,你能找到规律吗?
…
A
B
C
D
E1
E2
En
当有n个拐点时:
∠A+∠ E1 + ∠ E2 +…+
∠ En +∠C = 180°(n+1)
例1 如图,直线AB,CD被直线EF所截,
AB//CD, ∠ 1=100°,试求∠ 3的度数.
解 因为AB//CD,
所以∠ 1= ∠ 2=100°
(两直线平行,同位角相等).
又因为∠ 2+ ∠ 3=180°,
所以∠ 3=180°- ∠ 2=180°-100°=80°.
在例1中,分别利用平行线的性质2和性质3求出∠ 3的度数.
①如图所示,因为AB∥CD,
所以∠ 5= ∠ 1=100°
(两直线平行,内错角相等).
因为∠ 5+ ∠ 3=180°,
所以∠ 3=180°- ∠ 5=180°-100°=80°.
②如图所示,因为AB//CD,
所以∠ 1+∠ 4=180°
(两直线平行,同旁内角互补).
因为∠ 1=100°,所以∠ 4=180°-100°=80°.
因为∠ 3= ∠ 4(对顶角相等),所以∠ 3=80°.
例2 如图,AD//BC, ∠ B= ∠ D,
试问∠ A与∠ C相等吗?为什么?
解 因为AD//BC,
所以根据平行线的性质3可得:
∠ A+ ∠ B=180°, ∠ D+ ∠ C=180°.
又因为∠ B= ∠ D(已知),
所以∠ A= ∠ C.
1 填空:
(1)如图,因为AB//CD,所以∠1= ,
理由是 ;
(2)如图,因为AB//CD,所以∠D= ,
理由是 .
∠ A
∠ 2
两直线平行,同位角相等
两直线平行,内错角相等
2 如图,AB//CD//EF,BC//ED, ∠ B=70°,求∠ C, ∠ D和∠ E的度数.
∠ C=70°,
∠ D=110°,
∠ E=110°.
3 如图,直线AB,CD被直线EF所截,AB//CD,
∠ 1=105°,求∠ 2, ∠ 3, ∠ 4的度数.
∠ 2 =105°,
∠ 3=75°,
∠ 4=105°.
4 如图,已知AB//CD,AP平分∠ BAC,CP平分∠ ACD,
∠ 1+ ∠ 2=90°吗?
∠ 1+ ∠ 2=90°.
1.如图,已知平行线AB、CD被直线AE所截.
(1)从 ∠1=110o可以知道∠2 是多少度,为什么?
(2)从∠1=110o可以知道 ∠3是多少度,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度,为什么?
2
3
E
1
4
A
B
D
C
解:( 1 ) ∠2=110o
∵两直线行,内错角相等;
(2)∠3=110o
∵两直线平行, 同位角相等;
(3) ∠4=70o
∵两直线平行,同旁内角互补.
2
3
E
1
4
A
B
D
C
解:∠C=142o
∵两直线平行,内错角相等.
B
C
2.如图,一条公路两次拐弯前后两条路互相平行.
第一次拐的∠B是142o,第二次拐的∠C是多少度?为什么?
3.如图直线 a ∥ b,直线 b 垂直于直线 c ,
则直线 a 垂直于直线c 吗
a
b
c
解: a ⊥ c .
∵两直线平行, 同位角相等.
4.如果有两条直线被第三条直线所截,那么必定有( )
A.内错角相等.
B.同位角相等.
C.同旁内角互补.
D.以上都不对.
D
5.如图1,若AB∥DE ,AC∥DF,
请说出∠A和∠D之间的数量关系,并说明理由.
解: ∠A =∠D.理由:
∵ AB∥DE( )
∴∠A=_______ ( )
P
F
C
E
B
A
D
图1
已知
∠CPE
两直线平行,同位角相等
∵AC∥DF( )
∴∠D=______ ( )
∴∠A=∠D ( )
P
F
C
E
B
A
D
图1
已知
∠CPE
两直线平行,同位角相等
等量代换
如图2,若AB∥DE ,AC∥DF,
请说出∠A和∠D之间的数量关系,并说明理由.
解: ∠A+∠D=180o. 理由:
∵ AB∥DE( )
∴∠A= ______ ( )
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
∵AC∥DF( )
∴∠D+ _______=180o( )
∴∠A+∠D=180o( )
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同旁内角互补
等量代换
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
4.3 平行线的性质
1.平移前后的图形的形状和大小完全相同;
2.对应线段平行且相等.
平移的概念
平移的性质
平移
问题1 同一平面内两条直线的位置关系有哪几种?
问题2 直线平行的定义是什么?
问题3 你学了平行线的哪些内容?
相交(包括垂直)、重合和平行.
在同一平面内,不相交的两条直线平行.
平行于同一条直线的两条直线平行.
过直线外一点有且只有一条直线与这条直线平行.
如图,已知AB∥CD.
(1)图中有几对同位角?
(2)比较其中一对同位角的大小,
由此你能猜想出什么结论?
由图可知,图中有4对同位角.
经比较,可以发现每对同位角都相等,
并由此猜想:
如果两条平行直线被第三条直线所截,那么同位角相等.
下面来说明这个猜想是真的.
如图,直线AB与直线CD平行,
它们被直线EF所截,
交点分别为点M,N,
则∠EMB和∠END是一对同位角,
分别记作∠α和∠β.
将直线AB平移,
移动方向为点M到点N的方向,
移动距离等于线段MN的长度,
则点M的对应点是点N,
射线ME的像是射线NE,
直线AB的像是与它平行且经过点N的直线.
又已知CD∥AB且CD经过点N,
根据平行线的基本事实得,
直线AB的像是直线CD,
从而射线MB的像是射线ND,
于是∠α的像是∠β.
根据平移的知识得,∠α=∠β.
若AB与CD不平行,则∠α与∠β还会相等吗?
A
B
C
D
α
β
由此可得平行线的性质1:
两条平行直线被第三条
直线所截,同位角相等.
通常简单说成:
两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
小明在纸上画了一个角∠A,准备用量角器测量它的度数时,因不小心将纸片撕破,只剩下如图的一部分,如果不能延长DC、FE的话,你能帮他测出∠A的度数吗?
D
C
E
F
A
A
G
G
1
2
两条平行直线被第三条直线所截,一对内错角的大小有什么关系?
之前的学习中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”.
类似的,已知两直线平行,同位角相等, 那么能否推出内错角之间的数量关系?
如图,两条平行直线AB,CD被直线EF所截, ∠ 1与∠ 2是内错角.
因为AB∥CD,
所以∠ 1= ∠ 4(两直线平行,同位角相等).
又因为∠ 2= ∠ 4(对顶角相等),
所以∠ 1= ∠ 2(等量代换).
A
B
C
D
E
F
由此可得平行线的性质2:
两条平行直线被第三条
直线所截,内错角相等.
通常简单说成:
两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
如图,AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?
B
D
C
E
A
解:过点E 作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
F
B
D
C
E
A
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB.
F
A
B
C
D
E
当左边有两个角,右边有一个角时:
∠A+∠C= ∠E
变式:如图,AB∥CD, 则:
如图,AB∥CD, 则:
当左边有两个角,右边有两个角时:
∠A+∠F= ∠E +∠D
C
A
B
D
E
F
如图,AB∥CD, 则:
当左边有三个角,右边有两个角时:
∠A+∠F1 +∠C =∠ E1+∠E2
E1
C
A
B
D
E2
F1
如图,AB∥CD,若左边有n个角,右边有m个角;你能找到规律吗?
当左边有n个角,右边有m个角时:
∠A+∠F1 + ∠ F2 +…+ ∠Fn= ∠E1 +∠E2 +…+ ∠Em+ ∠D
C
A
B
D
E1
F1
E2
Em
F2
Fn
两条平行直线被第三条直线所截,
一对同旁内角有什么关系?
为什么?
如图, ∠ 1与∠ 3是同旁内角.
因为AB//CD,
所以∠ 1= ∠ 4(两直线平行,同位角相等).
又因为∠ 3+ ∠ 4=180°,
所以∠ 1+ ∠ 3=180°(等量代换).
A
B
C
D
E
F
由此可得平行线的性质3:
两条平行直线被第三条
直线所截,同旁内角互补.
通常简单说成:
两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180°
(两直线平行,同旁内角互补)
∵a∥b(已知)
应用格式:
1.如图,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
A
B
C
D
解:因为梯形上、下底互相平行,所以
∠A与∠D互补, ∠B与∠C互补.
于是∠D=180 °-∠A=180°-100°=80°.
∠C= 180 °-∠B=180°-115°=65°.
解:过点E 作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD.
∴EF//CD.
F
2.如图,AB//CD,探索∠B、∠D与∠DEB的大小关系 .
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°.
F
变式:如图所示,AB∥CD,则 :
C
A
B
D
E
当有一个拐点时:
∠A+∠E+∠C= 360°
如图所示,AB∥CD,则 :
A
C
D
B
E2
E1
当有两个拐点时:
∠A+∠ E1 + ∠ E2 +∠C = 540°
如图所示,AB∥CD,则 :
当有三个拐点时:
∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
A
B
C
D
E1
E2
E3
如图所示,AB∥CD,若有n个拐点,你能找到规律吗?
…
A
B
C
D
E1
E2
En
当有n个拐点时:
∠A+∠ E1 + ∠ E2 +…+
∠ En +∠C = 180°(n+1)
例1 如图,直线AB,CD被直线EF所截,
AB//CD, ∠ 1=100°,试求∠ 3的度数.
解 因为AB//CD,
所以∠ 1= ∠ 2=100°
(两直线平行,同位角相等).
又因为∠ 2+ ∠ 3=180°,
所以∠ 3=180°- ∠ 2=180°-100°=80°.
在例1中,分别利用平行线的性质2和性质3求出∠ 3的度数.
①如图所示,因为AB∥CD,
所以∠ 5= ∠ 1=100°
(两直线平行,内错角相等).
因为∠ 5+ ∠ 3=180°,
所以∠ 3=180°- ∠ 5=180°-100°=80°.
②如图所示,因为AB//CD,
所以∠ 1+∠ 4=180°
(两直线平行,同旁内角互补).
因为∠ 1=100°,所以∠ 4=180°-100°=80°.
因为∠ 3= ∠ 4(对顶角相等),所以∠ 3=80°.
例2 如图,AD//BC, ∠ B= ∠ D,
试问∠ A与∠ C相等吗?为什么?
解 因为AD//BC,
所以根据平行线的性质3可得:
∠ A+ ∠ B=180°, ∠ D+ ∠ C=180°.
又因为∠ B= ∠ D(已知),
所以∠ A= ∠ C.
1 填空:
(1)如图,因为AB//CD,所以∠1= ,
理由是 ;
(2)如图,因为AB//CD,所以∠D= ,
理由是 .
∠ A
∠ 2
两直线平行,同位角相等
两直线平行,内错角相等
2 如图,AB//CD//EF,BC//ED, ∠ B=70°,求∠ C, ∠ D和∠ E的度数.
∠ C=70°,
∠ D=110°,
∠ E=110°.
3 如图,直线AB,CD被直线EF所截,AB//CD,
∠ 1=105°,求∠ 2, ∠ 3, ∠ 4的度数.
∠ 2 =105°,
∠ 3=75°,
∠ 4=105°.
4 如图,已知AB//CD,AP平分∠ BAC,CP平分∠ ACD,
∠ 1+ ∠ 2=90°吗?
∠ 1+ ∠ 2=90°.
1.如图,已知平行线AB、CD被直线AE所截.
(1)从 ∠1=110o可以知道∠2 是多少度,为什么?
(2)从∠1=110o可以知道 ∠3是多少度,为什么?
(3)从 ∠1=110o可以知道∠4 是多少度,为什么?
2
3
E
1
4
A
B
D
C
解:( 1 ) ∠2=110o
∵两直线行,内错角相等;
(2)∠3=110o
∵两直线平行, 同位角相等;
(3) ∠4=70o
∵两直线平行,同旁内角互补.
2
3
E
1
4
A
B
D
C
解:∠C=142o
∵两直线平行,内错角相等.
B
C
2.如图,一条公路两次拐弯前后两条路互相平行.
第一次拐的∠B是142o,第二次拐的∠C是多少度?为什么?
3.如图直线 a ∥ b,直线 b 垂直于直线 c ,
则直线 a 垂直于直线c 吗
a
b
c
解: a ⊥ c .
∵两直线平行, 同位角相等.
4.如果有两条直线被第三条直线所截,那么必定有( )
A.内错角相等.
B.同位角相等.
C.同旁内角互补.
D.以上都不对.
D
5.如图1,若AB∥DE ,AC∥DF,
请说出∠A和∠D之间的数量关系,并说明理由.
解: ∠A =∠D.理由:
∵ AB∥DE( )
∴∠A=_______ ( )
P
F
C
E
B
A
D
图1
已知
∠CPE
两直线平行,同位角相等
∵AC∥DF( )
∴∠D=______ ( )
∴∠A=∠D ( )
P
F
C
E
B
A
D
图1
已知
∠CPE
两直线平行,同位角相等
等量代换
如图2,若AB∥DE ,AC∥DF,
请说出∠A和∠D之间的数量关系,并说明理由.
解: ∠A+∠D=180o. 理由:
∵ AB∥DE( )
∴∠A= ______ ( )
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
∵AC∥DF( )
∴∠D+ _______=180o( )
∴∠A+∠D=180o( )
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同旁内角互补
等量代换
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
同课章节目录
