4.4.1 平行线的判定方法1 课件(共33张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 4.4.1 平行线的判定方法1 课件(共33张PPT)2024-2025学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 00:00:00 | ||
图片预览







文档简介
(共33张PPT)
4.4 平行线的判定
4.4.1 平行线的判定方法1
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
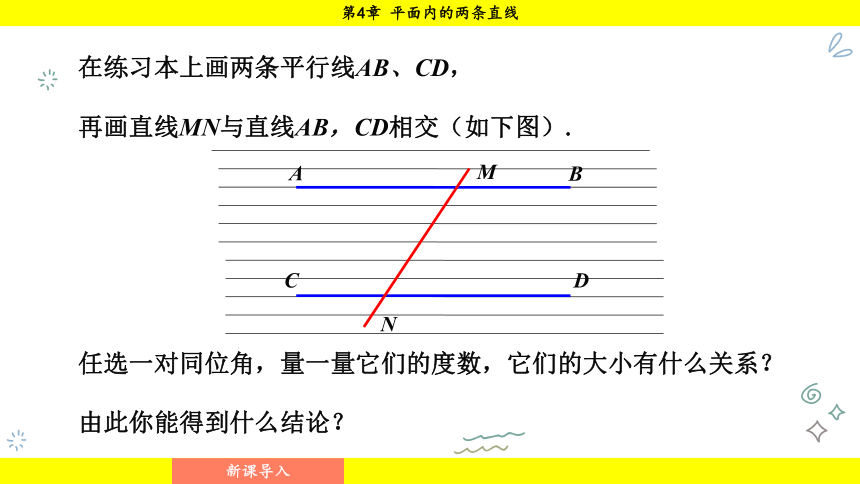
在练习本上画两条平行线AB、CD,
再画直线MN与直线AB,CD相交(如下图).
任选一对同位角,量一量它们的度数,它们的大小有什么关系?
由此你能得到什么结论?
A
B
C
D
M
N
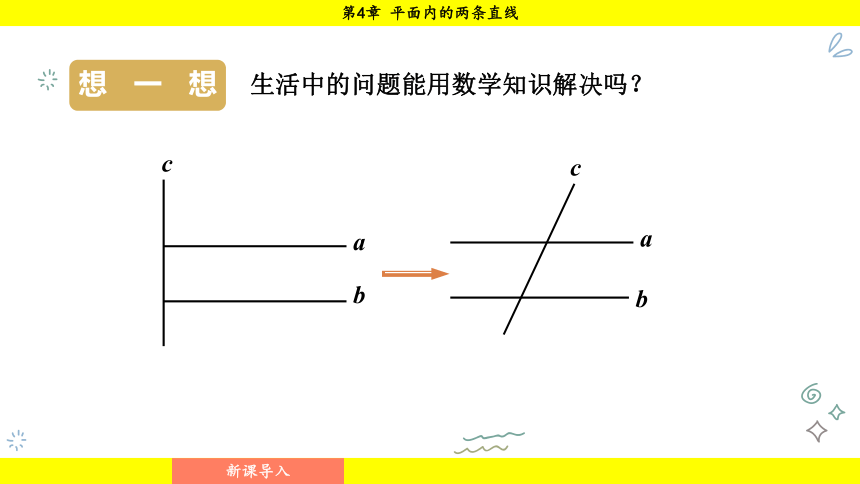
如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角是多少度时,才能使木条a与木条b平行?
生活中的问题能用数学知识解决吗?
a
c
b
a
b
c
想一想
由于直线是无限延伸的,因而利用平行线的定义判断两直线互相平行比较困难.
下面我们来寻求平行线的判定的其他方法.
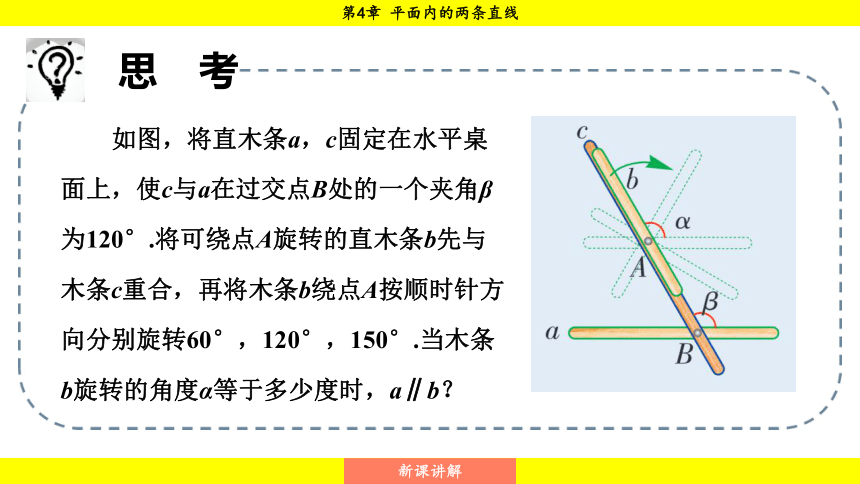
如图,将直木条a,c固定在水平桌面上,使c与a在过交点B处的一个夹角β为120°.将可绕点A旋转的直木条b先与木条c重合,再将木条b绕点A按顺时针方向分别旋转60°,120°,150°.当木条b旋转的角度α等于多少度时,a∥b?
当 ∠α =60°<∠β时,
当 ∠α =120°=∠β时,
当 ∠α =150°>∠β时,
直线a和b不平行
直线 a和b平行
直线a和b不平行
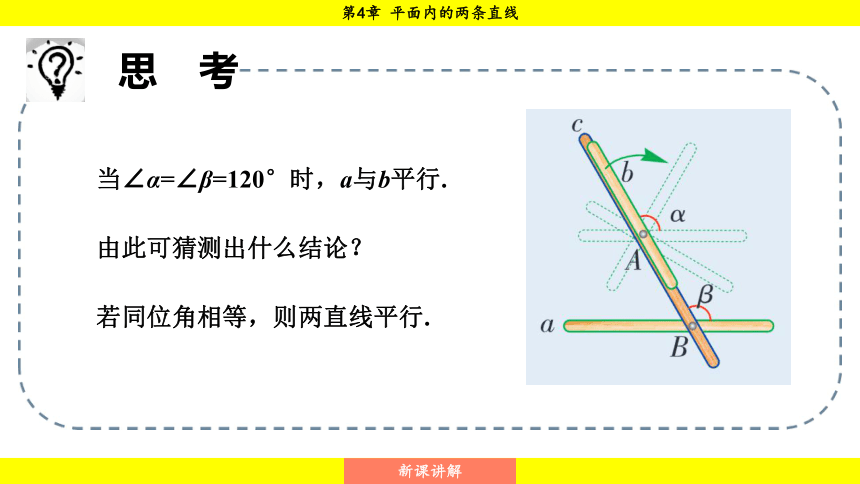
当∠α=∠β=120°时,a与b平行.
由此可猜测出什么结论?
若同位角相等,则两直线平行.
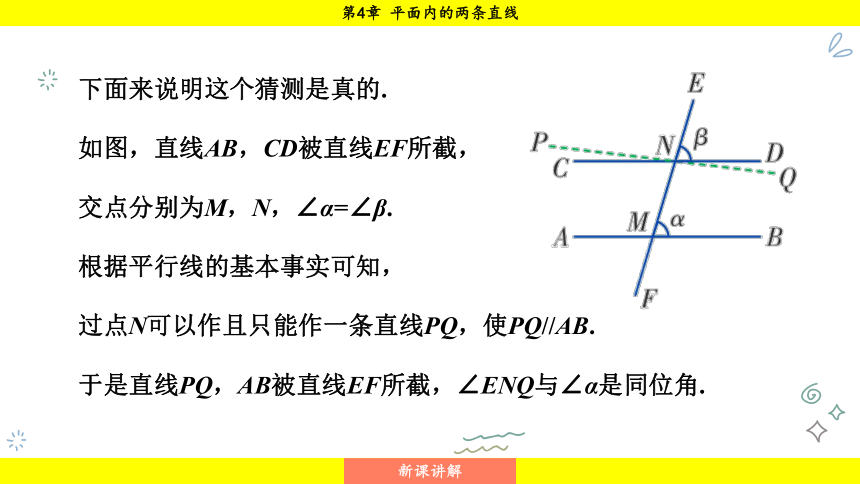
下面来说明这个猜测是真的.
如图,直线AB,CD被直线EF所截,
交点分别为M,N,∠α=∠β.
根据平行线的基本事实可知,
过点N可以作且只能作一条直线PQ,使PQ//AB.
于是直线PQ,AB被直线EF所截,∠ENQ与∠α是同位角.
根据平行线的性质1得, ∠ENQ =∠α.
由于∠α = ∠β,
因此∠ENQ= ∠β ,从而射线NQ与射线ND重合,
于是直线PQ与直线CD重合,
因此CD//AB.
由此可得平行线的判定方法1:
两条直线被第三条直线所截,如果
同位角相等,那么这两条直线平行.
通常简单说成:
同位角相等,两直线平行.
任画一条直线,用三角板和直尺画它的一条平行线,并说明该画法的原理.
●
一、放
二、靠
三、推
四、画
●
问题 在画图过程中,三角板起着什么样的作用?
b
A
2
1
a
B
(1)这样的画法可以看作是怎样的图形变换?
(2)画图过程中,什么角始终保持相等?
(3)将其最初和最终的特殊位置抽象成几何图形:
1
2
l2
l1
A
B
∵∠1=∠2(已知)
∴l1∥l2
(同位角相等,两直线平行)
1
2
l2
l1
A
B
应用格式:
下图中若∠1=55°,∠2=55°,
直线AB、CD平行吗?为什么
A
C
E
F
B
D
1
2
同位角相等,
两直线平行.
变式1:如图, ∠1=55 , ∠2=125 ,
直线AB与CD平行吗?为什么
A
C
E
F
B
D
1
2
M
N
同位角相等,两直线平行.
变式2:如图, 直线AB与CD被直线EF所截,∠1=55 ,
请添加一个条件使得直线AB与直线CD平行.
A
C
E
F
B
D
1
3
2
5
4
∠5=55
例1 如图,直线AB,CD被直线EF所截,
∠1+∠2=180°,那么AB//CD吗?
解 因为∠ 1+ ∠ 2=180°,
而∠ 3是∠ 1的补角,即∠ 1+ ∠ 3=180°,
所以∠ 2= ∠ 3.
所以AB//CD(同位角相等,两直线平行).
例2 如图,直线a,b被直线c,d所截,
∠ 1= ∠ 2,那么∠ 4= ∠ 5吗?
解 因为∠ 1= ∠ 2(已知),
∠ 2= ∠ 3(对顶角相等),
所以∠ 1= ∠ 3(等量代换).
所以a//b(同位角相等,两直线平行).
因此∠ 4= ∠ 5(两直线平行,同位角相等).
如图,已知AB∥DC,∠D=125°,∠CBE=55°,AD与BC平行吗?为什么?
解析:根据AB∥DC及∠D=125°,可求出∠A的度数,从而说明∠A=∠CBE.再根据同位角相等,两直线平行可得AD∥BC.
B
A
D
C
E
解:AD∥BC.
理由如下:因为AB∥DC(已知),
所以∠A+∠D=180°
(两直线平行,同旁内角互补).
因为∠D=125°(已知),
所以∠A=180°-∠D
=180°-125°
=55°.
因为∠CBE=55°(已知),
所以∠A=∠CBE,
所以AD∥BC(同位角相等,两直线平行).
1 如图,木工用直角尺的一边紧靠木料边缘,沿另一边画两条直线a,b.直线a,b平行吗?为什么?
解:平行.
同位角相等,两直线平行.
2 请在下面的括号内填写理由:
如图,已知三条直线a,b,c,
因为a//b,b//c,
所以∠ 1= ∠ 2, ∠ 2= ∠ 3,
因此∠ 1= ∠ 3.
从而a//c( ).
同位角相等,两直线平行
1.从∠5=∠ ,可以推出 AB∥CD,
理由是 .
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
2.如图所示,已知直线EF和AB,CD分别相交于K,H,且∠EGB=90°,∠CHF=60°,∠E=30°,试说明AB∥CD.
解:因为∠EGB=90° ,∠E=30°,
所以∠EKG=180°-90°-∠E=60°,
所以∠AKF=∠EKG=60°=∠CHF,
所以AB∥CD.
由同位角的关系判断两直线平行的三个步骤:
1.判断两个同位角是否相等.
2.若相等判断截线和被截直线.
3.得出两条被截直线平行.
4.4 平行线的判定
4.4.1 平行线的判定方法1
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
在练习本上画两条平行线AB、CD,
再画直线MN与直线AB,CD相交(如下图).
任选一对同位角,量一量它们的度数,它们的大小有什么关系?
由此你能得到什么结论?
A
B
C
D
M
N
如图,装修工人正在向墙上钉木条.如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角是多少度时,才能使木条a与木条b平行?
生活中的问题能用数学知识解决吗?
a
c
b
a
b
c
想一想
由于直线是无限延伸的,因而利用平行线的定义判断两直线互相平行比较困难.
下面我们来寻求平行线的判定的其他方法.
如图,将直木条a,c固定在水平桌面上,使c与a在过交点B处的一个夹角β为120°.将可绕点A旋转的直木条b先与木条c重合,再将木条b绕点A按顺时针方向分别旋转60°,120°,150°.当木条b旋转的角度α等于多少度时,a∥b?
当 ∠α =60°<∠β时,
当 ∠α =120°=∠β时,
当 ∠α =150°>∠β时,
直线a和b不平行
直线 a和b平行
直线a和b不平行
当∠α=∠β=120°时,a与b平行.
由此可猜测出什么结论?
若同位角相等,则两直线平行.
下面来说明这个猜测是真的.
如图,直线AB,CD被直线EF所截,
交点分别为M,N,∠α=∠β.
根据平行线的基本事实可知,
过点N可以作且只能作一条直线PQ,使PQ//AB.
于是直线PQ,AB被直线EF所截,∠ENQ与∠α是同位角.
根据平行线的性质1得, ∠ENQ =∠α.
由于∠α = ∠β,
因此∠ENQ= ∠β ,从而射线NQ与射线ND重合,
于是直线PQ与直线CD重合,
因此CD//AB.
由此可得平行线的判定方法1:
两条直线被第三条直线所截,如果
同位角相等,那么这两条直线平行.
通常简单说成:
同位角相等,两直线平行.
任画一条直线,用三角板和直尺画它的一条平行线,并说明该画法的原理.
●
一、放
二、靠
三、推
四、画
●
问题 在画图过程中,三角板起着什么样的作用?
b
A
2
1
a
B
(1)这样的画法可以看作是怎样的图形变换?
(2)画图过程中,什么角始终保持相等?
(3)将其最初和最终的特殊位置抽象成几何图形:
1
2
l2
l1
A
B
∵∠1=∠2(已知)
∴l1∥l2
(同位角相等,两直线平行)
1
2
l2
l1
A
B
应用格式:
下图中若∠1=55°,∠2=55°,
直线AB、CD平行吗?为什么
A
C
E
F
B
D
1
2
同位角相等,
两直线平行.
变式1:如图, ∠1=55 , ∠2=125 ,
直线AB与CD平行吗?为什么
A
C
E
F
B
D
1
2
M
N
同位角相等,两直线平行.
变式2:如图, 直线AB与CD被直线EF所截,∠1=55 ,
请添加一个条件使得直线AB与直线CD平行.
A
C
E
F
B
D
1
3
2
5
4
∠5=55
例1 如图,直线AB,CD被直线EF所截,
∠1+∠2=180°,那么AB//CD吗?
解 因为∠ 1+ ∠ 2=180°,
而∠ 3是∠ 1的补角,即∠ 1+ ∠ 3=180°,
所以∠ 2= ∠ 3.
所以AB//CD(同位角相等,两直线平行).
例2 如图,直线a,b被直线c,d所截,
∠ 1= ∠ 2,那么∠ 4= ∠ 5吗?
解 因为∠ 1= ∠ 2(已知),
∠ 2= ∠ 3(对顶角相等),
所以∠ 1= ∠ 3(等量代换).
所以a//b(同位角相等,两直线平行).
因此∠ 4= ∠ 5(两直线平行,同位角相等).
如图,已知AB∥DC,∠D=125°,∠CBE=55°,AD与BC平行吗?为什么?
解析:根据AB∥DC及∠D=125°,可求出∠A的度数,从而说明∠A=∠CBE.再根据同位角相等,两直线平行可得AD∥BC.
B
A
D
C
E
解:AD∥BC.
理由如下:因为AB∥DC(已知),
所以∠A+∠D=180°
(两直线平行,同旁内角互补).
因为∠D=125°(已知),
所以∠A=180°-∠D
=180°-125°
=55°.
因为∠CBE=55°(已知),
所以∠A=∠CBE,
所以AD∥BC(同位角相等,两直线平行).
1 如图,木工用直角尺的一边紧靠木料边缘,沿另一边画两条直线a,b.直线a,b平行吗?为什么?
解:平行.
同位角相等,两直线平行.
2 请在下面的括号内填写理由:
如图,已知三条直线a,b,c,
因为a//b,b//c,
所以∠ 1= ∠ 2, ∠ 2= ∠ 3,
因此∠ 1= ∠ 3.
从而a//c( ).
同位角相等,两直线平行
1.从∠5=∠ ,可以推出 AB∥CD,
理由是 .
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
2.如图所示,已知直线EF和AB,CD分别相交于K,H,且∠EGB=90°,∠CHF=60°,∠E=30°,试说明AB∥CD.
解:因为∠EGB=90° ,∠E=30°,
所以∠EKG=180°-90°-∠E=60°,
所以∠AKF=∠EKG=60°=∠CHF,
所以AB∥CD.
由同位角的关系判断两直线平行的三个步骤:
1.判断两个同位角是否相等.
2.若相等判断截线和被截直线.
3.得出两条被截直线平行.
同课章节目录
