4.5.2 垂线段与点到直线的距离 课件(共45张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 4.5.2 垂线段与点到直线的距离 课件(共45张PPT)2024-2025学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 00:00:00 | ||
图片预览









文档简介
(共45张PPT)
4.5 垂 线
4.5.2 垂线段与点到直线的距离
1.垂线的定义
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
2.垂线的性质
在平面内垂直于同一条两条直线平行.
在平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线必垂直于另一条.
在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
(1)画已知直线的垂线能画几条
(2)过直线上的一点画直线的垂线,这样的垂线能画几条
(3)过直线外的一点画直线的垂线,这样的垂线能画几条
.
.
任画一条直线 l,用三角板或量角器过任意一点 P 画直线 l 的垂线.
l
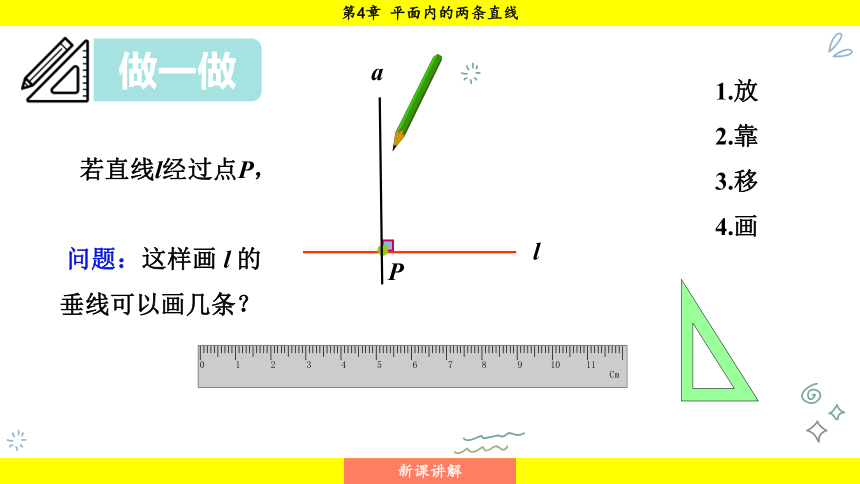
若直线l经过点P,
l
P
a
1.放
2.靠
3.移
4.画
问题:这样画 l 的垂线可以画几条?
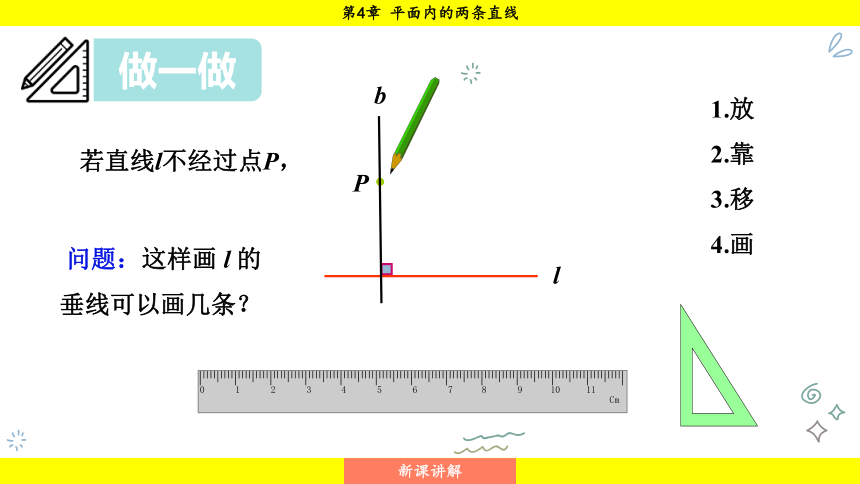
若直线l不经过点P,
l
P
b
1.放
2.靠
3.移
4.画
问题:这样画 l 的垂线可以画几条?
若直线 l 经过点 P,
则直线 l 的垂线 a 的画法如图所示.
若直线l不经过点P,
则直线l的垂线b的画法如图所示.
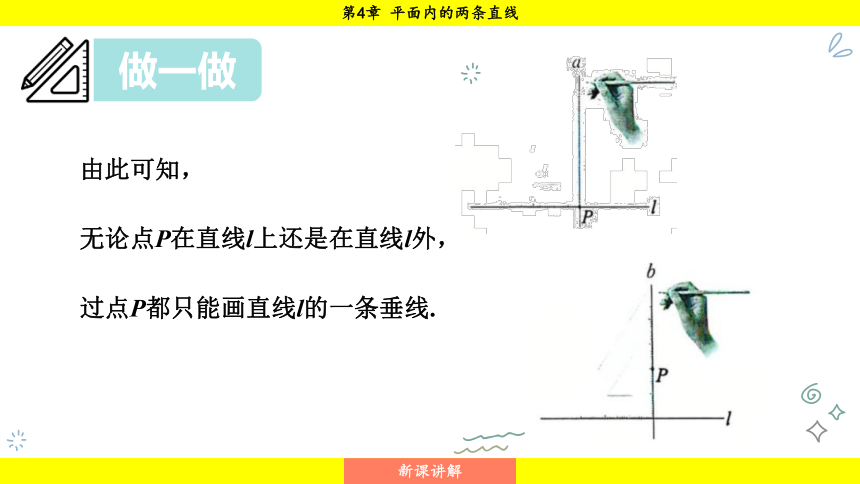
由此可知,
无论点P在直线l上还是在直线l外,
过点P都只能画直线l的一条垂线.
理由如下:
假如过点P还有一条直线c,能使c⊥l,
则c//a(或c//b).
又直线c与直线a(或直线b)有公共点P,
因此这是不可能的.
于是,可得关于垂线的基本事实:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
注意:
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
如图,设 PO 垂直于直线 l ,O 为垂足,线段 PO 叫作点 P 到直线 l 的垂线段.
经过点 P 的其他直线分别交直线 l 于点 A,B,C,D,…,线段 PA,PB,PC,PD,…都不是垂线段,称为斜线段.
比较图中 PA,PB,PO,PC,PD 五条线段的长度,哪条线段最短?
通过比较,我发现垂线段PO最短.
数学上已经证明这一发现是正确的.
你能用一句话表示这个结论吗?
通过比较,我发现垂线段PO最短.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
通常简单说成:垂线段最短.
从直线外一点到这条直线的垂线段的长度,
叫作点到直线的距离,
例如,图中,垂线段PO的长度叫作点P到直线l的距离.
让我们回到本节课开始时提出的问题:
在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?
m
垂线段最短
如图,三角形ABC中,∠C=90°.
(1)分别指出点A到直线BC,点B到
直线AC的距离是哪些线段的长?
(2)三条边AB、AC、BC中哪条边最长?
为什么?
(1)点A到直线BC的距离是线段AC的长,
点B到直线AC的距离是线段BC的长.
(2)三条边AB、AC、BC中AB最长.
理由:连接线段外一点与线段上各点
的所有线段中,垂线段最短.
(1)量出图中点P到直线AB的距离.
(2)某单位要在河岸l上建一个水泵房引水到C处,如图所示,问建在哪个位置才最节省水管?
为什么?
如图所示,过点C作CA⊥l,垂足为A,这时在河岸l上的A处建一个水泵房引水到C处,才最节省水管.
直线外一点与直线上各点连接
的所有线段中,垂线段最短.
(3)由(1)(2)你会发现可以怎样求点到直线的距离?
由(1)(2)可知,
求点到直线的距离可以转化为求点到点的距离.
例3 如图,在△ABC中,∠ABC=90°,BD⊥AC,垂足为点D,AB=5,BC=12,AC=13.求:
(1)点A到直线BC的距离;
(2)点B到直线AC的距离.
解(1)因为∠ABC=90°,
所以AB⊥BC,点B为垂足,
所以线段AB即为点A到直线BC的垂线段.
因为AB=5,
所以点A到直线BC的距离为5.
(2)因为BD⊥AC,垂足为点D,
所以线段BD的长度即为点B到直线AC的距离.
因为S△ABC = ·BC·AB = ·AC·BD,
所以BD = = = .
所以点B到直线AC的距离为 .
1 如图,在△ABC中,∠A=90°,AB=3,AC=4,BC=5,求点A到
BC的距离,点C到AB的距离.
解:过点A作AD⊥BC,垂足为D,所以线段AD的长度即为点A到BC的距离.
因为 AB·AC= AD·BC,
所以AD= = .
D
因为∠BAC=90°,所以CA⊥AB.
所以线段AC的长度
即为点C到AB的距离.
所以点A到BC的距离是 ,点C到AB的距离是4.
D
2 某公园的4条纵横交错的人行道和一喷泉的示意图如图所示(比例
尺为1:5000),其中直线a,b,c,d表示人行道,点P表示喷泉.
量出点P到4条直线的距离,
并求出其实际距离.
3 如图,体育课上应该怎样测量同学们的跳远成绩?
解:体育课上,测量同学们的跳远成绩的方法是先过落地点作起跳线的垂线,
然后量取落地点到起跳线的垂线段的长度,
此长度就是同学们的跳远成绩.
1.过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
2.如图, AB⊥CD,∠ACB=90°,线段AC、BC、CD中最短的是 ( )
A. AC
B. BC
C. CD
D. 不能确定
D
A
B
C
C
3. P 是直线 AB 外一点,过点 P 作 PO⊥AB ,垂足为 O ,若 C 为直线 AB 上任意一点,则线段 PC 与线段 PO 的大小关系是( )
A. PC > PO B. PC < PO
C. PC ≥ PO D. PC ≤ PO
C
A
B
C
D
D
4.下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫做点A到直线AC的距离
C.线段BD的长度叫做点D到直线BC的距离
D.线段BD的长度叫做点B到直线AC的距离
A
B
C
D
M
N
5.一辆汽车在直线形的公路AB上由A向B行驶,C、D 是分别位于公路AB两侧的加油站.
(1)设汽车行驶到公路AB上点M的位置时,
距离加油站C最近;行驶到点N的位置时,距离
加油站D最近,请在图中分别画出点M、N的位置;
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离C、D两加油站都越来越近?在哪一段路上距离加油站D越来越近,而离加油站C却越来越远?
在公路 AB 的 AM 段距离 C、D 两加油站都越来越近,在 MN 段距离加油站 D 越来越近,而加油站 C 却越来越远.
A
B
C
D
M
N
6.如图,平原上有A,B,C,D 四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水
池H 点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池 H 中,怎样开渠最短并说明根据.
H
解:(1)∵两点之间线段最短,
∴连接AD,BC 交于 H ,
则 H 为蓄水池位置,
它到四个村庄距离之和最小.
(2)过 H 作 HG⊥EF ,垂足为 G .
“过直线外一点与直线各点的连线中,垂线段最短”是把河水引入蓄水池 H 中开渠最短的根据.
G
H
1.垂线的画法
2.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直;
一、放;二、靠;三、移 ;四、画.
3.点到直线的距离
(2)垂线段最短.
4.5 垂 线
4.5.2 垂线段与点到直线的距离
1.垂线的定义
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足.
2.垂线的性质
在平面内垂直于同一条两条直线平行.
在平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线必垂直于另一条.
在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?请画出图来,并说明理由.
(1)画已知直线的垂线能画几条
(2)过直线上的一点画直线的垂线,这样的垂线能画几条
(3)过直线外的一点画直线的垂线,这样的垂线能画几条
.
.
任画一条直线 l,用三角板或量角器过任意一点 P 画直线 l 的垂线.
l
若直线l经过点P,
l
P
a
1.放
2.靠
3.移
4.画
问题:这样画 l 的垂线可以画几条?
若直线l不经过点P,
l
P
b
1.放
2.靠
3.移
4.画
问题:这样画 l 的垂线可以画几条?
若直线 l 经过点 P,
则直线 l 的垂线 a 的画法如图所示.
若直线l不经过点P,
则直线l的垂线b的画法如图所示.
由此可知,
无论点P在直线l上还是在直线l外,
过点P都只能画直线l的一条垂线.
理由如下:
假如过点P还有一条直线c,能使c⊥l,
则c//a(或c//b).
又直线c与直线a(或直线b)有公共点P,
因此这是不可能的.
于是,可得关于垂线的基本事实:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
注意:
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性.
如图,设 PO 垂直于直线 l ,O 为垂足,线段 PO 叫作点 P 到直线 l 的垂线段.
经过点 P 的其他直线分别交直线 l 于点 A,B,C,D,…,线段 PA,PB,PC,PD,…都不是垂线段,称为斜线段.
比较图中 PA,PB,PO,PC,PD 五条线段的长度,哪条线段最短?
通过比较,我发现垂线段PO最短.
数学上已经证明这一发现是正确的.
你能用一句话表示这个结论吗?
通过比较,我发现垂线段PO最短.
直线外一点与直线上各点连接的所有线段中,垂线段最短.
通常简单说成:垂线段最短.
从直线外一点到这条直线的垂线段的长度,
叫作点到直线的距离,
例如,图中,垂线段PO的长度叫作点P到直线l的距离.
让我们回到本节课开始时提出的问题:
在灌溉时,要把河中的水引到农田P处,如何挖掘能使渠道最短?
m
垂线段最短
如图,三角形ABC中,∠C=90°.
(1)分别指出点A到直线BC,点B到
直线AC的距离是哪些线段的长?
(2)三条边AB、AC、BC中哪条边最长?
为什么?
(1)点A到直线BC的距离是线段AC的长,
点B到直线AC的距离是线段BC的长.
(2)三条边AB、AC、BC中AB最长.
理由:连接线段外一点与线段上各点
的所有线段中,垂线段最短.
(1)量出图中点P到直线AB的距离.
(2)某单位要在河岸l上建一个水泵房引水到C处,如图所示,问建在哪个位置才最节省水管?
为什么?
如图所示,过点C作CA⊥l,垂足为A,这时在河岸l上的A处建一个水泵房引水到C处,才最节省水管.
直线外一点与直线上各点连接
的所有线段中,垂线段最短.
(3)由(1)(2)你会发现可以怎样求点到直线的距离?
由(1)(2)可知,
求点到直线的距离可以转化为求点到点的距离.
例3 如图,在△ABC中,∠ABC=90°,BD⊥AC,垂足为点D,AB=5,BC=12,AC=13.求:
(1)点A到直线BC的距离;
(2)点B到直线AC的距离.
解(1)因为∠ABC=90°,
所以AB⊥BC,点B为垂足,
所以线段AB即为点A到直线BC的垂线段.
因为AB=5,
所以点A到直线BC的距离为5.
(2)因为BD⊥AC,垂足为点D,
所以线段BD的长度即为点B到直线AC的距离.
因为S△ABC = ·BC·AB = ·AC·BD,
所以BD = = = .
所以点B到直线AC的距离为 .
1 如图,在△ABC中,∠A=90°,AB=3,AC=4,BC=5,求点A到
BC的距离,点C到AB的距离.
解:过点A作AD⊥BC,垂足为D,所以线段AD的长度即为点A到BC的距离.
因为 AB·AC= AD·BC,
所以AD= = .
D
因为∠BAC=90°,所以CA⊥AB.
所以线段AC的长度
即为点C到AB的距离.
所以点A到BC的距离是 ,点C到AB的距离是4.
D
2 某公园的4条纵横交错的人行道和一喷泉的示意图如图所示(比例
尺为1:5000),其中直线a,b,c,d表示人行道,点P表示喷泉.
量出点P到4条直线的距离,
并求出其实际距离.
3 如图,体育课上应该怎样测量同学们的跳远成绩?
解:体育课上,测量同学们的跳远成绩的方法是先过落地点作起跳线的垂线,
然后量取落地点到起跳线的垂线段的长度,
此长度就是同学们的跳远成绩.
1.过点P 向线段AB 所在直线引垂线,正确的是( )
A B C D
C
2.如图, AB⊥CD,∠ACB=90°,线段AC、BC、CD中最短的是 ( )
A. AC
B. BC
C. CD
D. 不能确定
D
A
B
C
C
3. P 是直线 AB 外一点,过点 P 作 PO⊥AB ,垂足为 O ,若 C 为直线 AB 上任意一点,则线段 PC 与线段 PO 的大小关系是( )
A. PC > PO B. PC < PO
C. PC ≥ PO D. PC ≤ PO
C
A
B
C
D
D
4.下列说法正确的是( )
A.线段AB叫做点B到直线AC的距离
B.线段AB的长度叫做点A到直线AC的距离
C.线段BD的长度叫做点D到直线BC的距离
D.线段BD的长度叫做点B到直线AC的距离
A
B
C
D
M
N
5.一辆汽车在直线形的公路AB上由A向B行驶,C、D 是分别位于公路AB两侧的加油站.
(1)设汽车行驶到公路AB上点M的位置时,
距离加油站C最近;行驶到点N的位置时,距离
加油站D最近,请在图中分别画出点M、N的位置;
(2)当汽车从A出发向B行驶时,在公路AB的哪一段路上距离C、D两加油站都越来越近?在哪一段路上距离加油站D越来越近,而离加油站C却越来越远?
在公路 AB 的 AM 段距离 C、D 两加油站都越来越近,在 MN 段距离加油站 D 越来越近,而加油站 C 却越来越远.
A
B
C
D
M
N
6.如图,平原上有A,B,C,D 四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池.
(1)不考虑其他因素,请你画图确定蓄水
池H 点的位置,使它到四个村庄距离之和最小;
(2)计划把河水引入蓄水池 H 中,怎样开渠最短并说明根据.
H
解:(1)∵两点之间线段最短,
∴连接AD,BC 交于 H ,
则 H 为蓄水池位置,
它到四个村庄距离之和最小.
(2)过 H 作 HG⊥EF ,垂足为 G .
“过直线外一点与直线各点的连线中,垂线段最短”是把河水引入蓄水池 H 中开渠最短的根据.
G
H
1.垂线的画法
2.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直;
一、放;二、靠;三、移 ;四、画.
3.点到直线的距离
(2)垂线段最短.
同课章节目录
