4.6 两条平行线间的距离 课件(共45张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 4.6 两条平行线间的距离 课件(共45张PPT)2024-2025学年数学湘教版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 16:34:20 | ||
图片预览










文档简介
(共45张PPT)
4.6 两条平行线间的距离
1.垂线的画法
2.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直;
一、放;二、靠;三、移 ;四、画.
3.点到直线的距离
(2)垂线段最短.
A
B
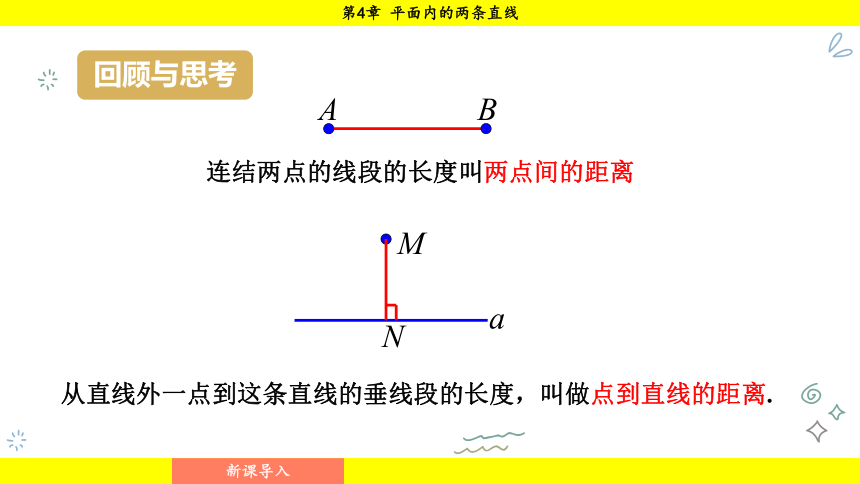
连结两点的线段的长度叫两点间的距离
M
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
N
a
回顾与思考
C 点到点的距离
A两平行线的距离
B点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
跳
远
的
成
绩
C 点到点的距离
A两平行线的距离
B点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
掷铅球
的
成
绩
C 点到点的距离
A两平行线的距离
B点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
直跑道间
距离
请各位同学用直尺量一量自己的数学课本,它的宽度是多少?
你的直尺与课本的两边成什么角度?量在课本的哪个位置?大家量得的结果是一样的吗?
可以把直尺放在课本上任何一个位置,必须保持直尺与课本的两边互相垂直,量得的结果是一样的.
画两条互相平行的直线,从其中一条直线上任取两点,比较这两点到另一条直线的距离.
再多取几个点,结果会发生变化吗?
由此你会发现什么?
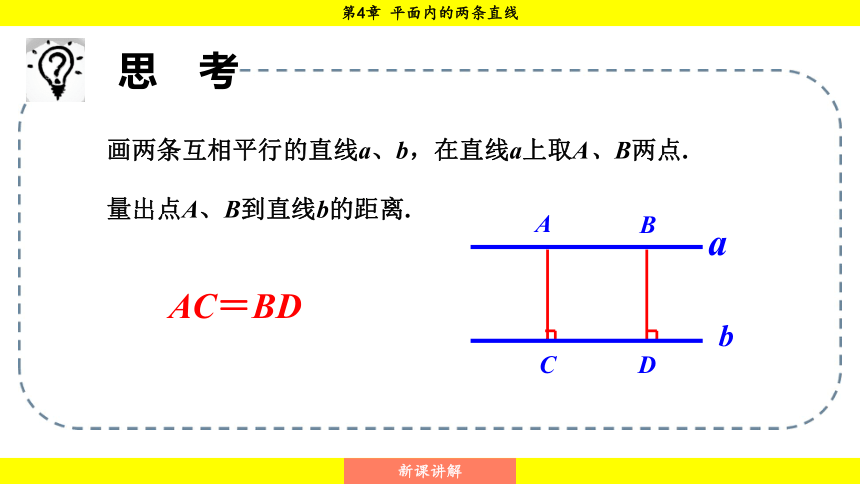
画两条互相平行的直线a、b,在直线a上取A、B两点.
量出点A、B到直线b的距离.
C
D
AC=BD
B
A
把一把三角尺的一条直角边沿着直线b移动,观察三角尺的另一条直角边与直线a交点处的刻度,刻度有改变吗?
a
b
如图,l1 // l2,
在直线 l1上任取两点A,C,
分别作AB⊥ l2 ,CD⊥ l2 ,
垂足分别为点B,D.
于是AB⊥ l1 ,CD⊥ l1.
图中的线段AB,CD都是平行线 l1 与 l2 的公垂线段.
概念学习
与两条平行直线都垂直的直线,叫作这两条平行直线的公垂线,
这时连接两个垂足的线段叫作这两条平行直线的公垂线段.
1.如图(1),已知m∥n,下列哪条为公垂线_____;
2.如图(2),已知m∥n,下列哪条为公垂线段_____.
m
n
m
n
a
b
A
B
E
C
D
F
┒
┒
b
CD
⑴
⑵
比较线段AB与CD的长度,
可以发现AB=CD.
再另取几个点,也会发现平行线
l1 与 l2 的公垂线段的长度相等,且均等于线段AB的长度,由此可得:
两条平行线的所有公垂线段都相等.
数学上已经证明上述结论是真的.
两条平行线的所有公垂线段都相等
设直线 l1 // l2,在l1上任取两点A,C,
过点A作 l2 的垂线,垂足为点B,过点C作
l2 的垂线,垂足为点D,如图所示.
由于AB⊥l2,CD⊥l2,因此AB∥CD.
将直线AB沿点A到点C的方向平移线段AC
的长度,则点A的对应点是点C,直线AB的像是
过点C且与AB平行的直线.根据平行线的基本事实得,直线AB的像就是直线CD.于是点B的对应点在直线CD上.
由于l1 // l2 ,因此l1的方向(从点A到点C的方向)与l2的方向
(从点B到点D的方向)相同,从而在上述平移下,点B的对应点在直线l2上,于是点B的对应点就是直线l2与直线CD的交点D.因此,线段AB的像是线段CD.
根据平移保持任意两点间距离不变可得,AB=CD.
这就说明了:两条平行线的所有公垂线段都相等.
两条平行线的所有公垂线段都 .
相等
几何语言:
∵a∥b,AB⊥b,CD⊥b
∴AB=CD
C
D
B
A
由上述结论可以进一步猜测:
平行线 l1 与 l2 之间的距离等于l1 任一点到直线 l2的距离.
结论:两条平行线的公垂线段的长度叫作两条平行线间的距离.
下面来说明这个猜测是真的.
如图,线段AB是两条平行线 l1 与 l2 的
公垂线段,从而线段AB的长度是直线 l1 与 l2
之间的距离.
又线段AB的长度是点A到直线 l2 的距离,
因此,平行线 l1 与 l2之间的距离等于直线 l1 上的点A到直线 l2的距离.
由此可知:
两条平行线间的距离等于其中一条直线上任意一个点到另一条直线的距离.
如图,设l1//l2,A,B分别为l1,l2上的任意点,连结线段AB,再过A作AC⊥l2,垂足为C,则AC是l1,l2之间的公垂线段,AB是l1,l2之间的斜线段.因为AC,AB又分别是A点到l2的垂线段和斜线段,所以AC < AB(垂线段最短).
两平行线上各取一点连接而成的所有线段中,公垂线段最短.
A
B
C
l1
l2
如图,已知AD//BC,判断 与 是否相等,并说明理由.
解:∵AD∥BC
∴△ABC与△DBC的高相等
∵ △ABC与△DBC的底都是BC
∴ △ABC与△DBC是同底等高
∴S△ABC=S△DBC
例1 如图,AB∥DC,AB=DC,DE⊥AB,BF⊥CD,
垂足分别为点E,F,那么线段AE与CF相等吗?
解 因为AB//DC,DE⊥AB,
所以DE⊥DC.
又AB//DC,BF⊥CD,
于是BF⊥AB.
因而DE//FB.
又DF⊥DE,DF⊥FB,EB⊥DE,EB⊥FB,
从而线段DF,EB都是平行线DE与FB的公垂线段.
故DF=EB.
又AB=DC,
所以AB-EB=DC-DF,即AE=CF.
例2 设a,b,c是三条互相平行的直线,如图所示.
已知a与b的距离为5,b与c的距离为2,求a与c的距离.
解 在a上任取一点A,过点A作AC⊥c,
分别与b,c相交于B,C两点.
因为a,b,c是三条互相平行的直线,
所以∠ 1= ∠ 2= ∠ 3=90°,
即AB⊥b,AC⊥a.
因此,线段AB,BC,AC分别是平行线a与b,b与c,a与c的公垂线段.
又AC=AB+BC=5+2=7,
因此,a与c的距离是7.
若将例2中的“如图所示”去掉,a与c的距离会变化吗?将你的结果与同学交流.
设a,b,c是三条互相平行的直线.
已知a与b的距离为5,b与c的距离为2,求a与c的距离.
(1)如图1,
∵AB=5, BC=2, ∴AC=7.
A
B
C
解:有两种情况.
图1
a
b
c
设a,b,c是三条互相平行的直线.已知a与b的距离为5,b与c的距离为2,求a与c的距离.
a
c
b
A
B
C
图2
(2)如图2 ,
∵AB=5, BC=2, ∴AC=3.
设a,b,c是三条互相平行的直线.
已知a与b的距离为5,b与c的距离为2,求a与c的距离.
1 利用平移画一条直线和已知直线 l 平行,且要求两条平行线间的距离
为 2 cm,这样的直线可以画几条?
解:可以画两条,如图所示.
2 如图,MN // AB,P,Q为直线 MN 上的任意两点,
△PAB 和 △QAB 的面积有什么关系?为什么?
解:相等.
因为△PAB和△QAB的AB边上的高相等,
都是MN与AB之间的距离,所以两个三
角形的面积相等.
C
1.两平行线的公垂线段有多少条?( )
A.1 B.2
C.无数条 D.一条也没有
2.点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5cm,则点M到AB的距离为( )
A.大于5 cm B.小于5 cm
C.5 cm D.不确定
C
3.如图,a⊥c,b⊥c,c交a,b于A、B两点,d交AB于C、D两点,且d与c不平行,
则AB CD(填“>”、“=”、“<”)
<
4.如图,长方形ABCD的宽AD的长度是2cm,
点P到AB的距离是1.6cm,
那么点P到CD的距离是_________.
3.6cm
5.如图,已知直线MN∥PQ,BC=4cm,
若三角形ABC的面积为6cm ,
则平行线MN,PQ的距离是 cm.
3
6.如图是山坡上两棵树,你能量出他们之间的距离吗
7.(1)如图,MN∥AB, P、Q为直线MN上的任意两点,
ΔPAB和ΔQAB的面积相等吗?
M P Q N
A B
相等
(2)如图,MN∥AB, P是MN上的一动点,P沿MN的方向每次移动1cm,当它移动10cm 时得到ΔP1AB,
那么ΔP1AB的面积是多少?
M P N
P1
A B
a cm2
a cm2
两条平行线间的距离
概念
性质
公垂线,公垂线段,
平行线间的距离
两条平行线的公垂线段都相等
4.6 两条平行线间的距离
1.垂线的画法
2.垂线的性质
(1)过一点有且只有一条直线与已知直线垂直;
一、放;二、靠;三、移 ;四、画.
3.点到直线的距离
(2)垂线段最短.
A
B
连结两点的线段的长度叫两点间的距离
M
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
N
a
回顾与思考
C 点到点的距离
A两平行线的距离
B点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
跳
远
的
成
绩
C 点到点的距离
A两平行线的距离
B点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
掷铅球
的
成
绩
C 点到点的距离
A两平行线的距离
B点到直线的距离
你能把现实生活中的活动用数学知识来解答吗?
测
量
直跑道间
距离
请各位同学用直尺量一量自己的数学课本,它的宽度是多少?
你的直尺与课本的两边成什么角度?量在课本的哪个位置?大家量得的结果是一样的吗?
可以把直尺放在课本上任何一个位置,必须保持直尺与课本的两边互相垂直,量得的结果是一样的.
画两条互相平行的直线,从其中一条直线上任取两点,比较这两点到另一条直线的距离.
再多取几个点,结果会发生变化吗?
由此你会发现什么?
画两条互相平行的直线a、b,在直线a上取A、B两点.
量出点A、B到直线b的距离.
C
D
AC=BD
B
A
把一把三角尺的一条直角边沿着直线b移动,观察三角尺的另一条直角边与直线a交点处的刻度,刻度有改变吗?
a
b
如图,l1 // l2,
在直线 l1上任取两点A,C,
分别作AB⊥ l2 ,CD⊥ l2 ,
垂足分别为点B,D.
于是AB⊥ l1 ,CD⊥ l1.
图中的线段AB,CD都是平行线 l1 与 l2 的公垂线段.
概念学习
与两条平行直线都垂直的直线,叫作这两条平行直线的公垂线,
这时连接两个垂足的线段叫作这两条平行直线的公垂线段.
1.如图(1),已知m∥n,下列哪条为公垂线_____;
2.如图(2),已知m∥n,下列哪条为公垂线段_____.
m
n
m
n
a
b
A
B
E
C
D
F
┒
┒
b
CD
⑴
⑵
比较线段AB与CD的长度,
可以发现AB=CD.
再另取几个点,也会发现平行线
l1 与 l2 的公垂线段的长度相等,且均等于线段AB的长度,由此可得:
两条平行线的所有公垂线段都相等.
数学上已经证明上述结论是真的.
两条平行线的所有公垂线段都相等
设直线 l1 // l2,在l1上任取两点A,C,
过点A作 l2 的垂线,垂足为点B,过点C作
l2 的垂线,垂足为点D,如图所示.
由于AB⊥l2,CD⊥l2,因此AB∥CD.
将直线AB沿点A到点C的方向平移线段AC
的长度,则点A的对应点是点C,直线AB的像是
过点C且与AB平行的直线.根据平行线的基本事实得,直线AB的像就是直线CD.于是点B的对应点在直线CD上.
由于l1 // l2 ,因此l1的方向(从点A到点C的方向)与l2的方向
(从点B到点D的方向)相同,从而在上述平移下,点B的对应点在直线l2上,于是点B的对应点就是直线l2与直线CD的交点D.因此,线段AB的像是线段CD.
根据平移保持任意两点间距离不变可得,AB=CD.
这就说明了:两条平行线的所有公垂线段都相等.
两条平行线的所有公垂线段都 .
相等
几何语言:
∵a∥b,AB⊥b,CD⊥b
∴AB=CD
C
D
B
A
由上述结论可以进一步猜测:
平行线 l1 与 l2 之间的距离等于l1 任一点到直线 l2的距离.
结论:两条平行线的公垂线段的长度叫作两条平行线间的距离.
下面来说明这个猜测是真的.
如图,线段AB是两条平行线 l1 与 l2 的
公垂线段,从而线段AB的长度是直线 l1 与 l2
之间的距离.
又线段AB的长度是点A到直线 l2 的距离,
因此,平行线 l1 与 l2之间的距离等于直线 l1 上的点A到直线 l2的距离.
由此可知:
两条平行线间的距离等于其中一条直线上任意一个点到另一条直线的距离.
如图,设l1//l2,A,B分别为l1,l2上的任意点,连结线段AB,再过A作AC⊥l2,垂足为C,则AC是l1,l2之间的公垂线段,AB是l1,l2之间的斜线段.因为AC,AB又分别是A点到l2的垂线段和斜线段,所以AC < AB(垂线段最短).
两平行线上各取一点连接而成的所有线段中,公垂线段最短.
A
B
C
l1
l2
如图,已知AD//BC,判断 与 是否相等,并说明理由.
解:∵AD∥BC
∴△ABC与△DBC的高相等
∵ △ABC与△DBC的底都是BC
∴ △ABC与△DBC是同底等高
∴S△ABC=S△DBC
例1 如图,AB∥DC,AB=DC,DE⊥AB,BF⊥CD,
垂足分别为点E,F,那么线段AE与CF相等吗?
解 因为AB//DC,DE⊥AB,
所以DE⊥DC.
又AB//DC,BF⊥CD,
于是BF⊥AB.
因而DE//FB.
又DF⊥DE,DF⊥FB,EB⊥DE,EB⊥FB,
从而线段DF,EB都是平行线DE与FB的公垂线段.
故DF=EB.
又AB=DC,
所以AB-EB=DC-DF,即AE=CF.
例2 设a,b,c是三条互相平行的直线,如图所示.
已知a与b的距离为5,b与c的距离为2,求a与c的距离.
解 在a上任取一点A,过点A作AC⊥c,
分别与b,c相交于B,C两点.
因为a,b,c是三条互相平行的直线,
所以∠ 1= ∠ 2= ∠ 3=90°,
即AB⊥b,AC⊥a.
因此,线段AB,BC,AC分别是平行线a与b,b与c,a与c的公垂线段.
又AC=AB+BC=5+2=7,
因此,a与c的距离是7.
若将例2中的“如图所示”去掉,a与c的距离会变化吗?将你的结果与同学交流.
设a,b,c是三条互相平行的直线.
已知a与b的距离为5,b与c的距离为2,求a与c的距离.
(1)如图1,
∵AB=5, BC=2, ∴AC=7.
A
B
C
解:有两种情况.
图1
a
b
c
设a,b,c是三条互相平行的直线.已知a与b的距离为5,b与c的距离为2,求a与c的距离.
a
c
b
A
B
C
图2
(2)如图2 ,
∵AB=5, BC=2, ∴AC=3.
设a,b,c是三条互相平行的直线.
已知a与b的距离为5,b与c的距离为2,求a与c的距离.
1 利用平移画一条直线和已知直线 l 平行,且要求两条平行线间的距离
为 2 cm,这样的直线可以画几条?
解:可以画两条,如图所示.
2 如图,MN // AB,P,Q为直线 MN 上的任意两点,
△PAB 和 △QAB 的面积有什么关系?为什么?
解:相等.
因为△PAB和△QAB的AB边上的高相等,
都是MN与AB之间的距离,所以两个三
角形的面积相等.
C
1.两平行线的公垂线段有多少条?( )
A.1 B.2
C.无数条 D.一条也没有
2.点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5cm,则点M到AB的距离为( )
A.大于5 cm B.小于5 cm
C.5 cm D.不确定
C
3.如图,a⊥c,b⊥c,c交a,b于A、B两点,d交AB于C、D两点,且d与c不平行,
则AB CD(填“>”、“=”、“<”)
<
4.如图,长方形ABCD的宽AD的长度是2cm,
点P到AB的距离是1.6cm,
那么点P到CD的距离是_________.
3.6cm
5.如图,已知直线MN∥PQ,BC=4cm,
若三角形ABC的面积为6cm ,
则平行线MN,PQ的距离是 cm.
3
6.如图是山坡上两棵树,你能量出他们之间的距离吗
7.(1)如图,MN∥AB, P、Q为直线MN上的任意两点,
ΔPAB和ΔQAB的面积相等吗?
M P Q N
A B
相等
(2)如图,MN∥AB, P是MN上的一动点,P沿MN的方向每次移动1cm,当它移动10cm 时得到ΔP1AB,
那么ΔP1AB的面积是多少?
M P N
P1
A B
a cm2
a cm2
两条平行线间的距离
概念
性质
公垂线,公垂线段,
平行线间的距离
两条平行线的公垂线段都相等
同课章节目录
