6.2.1 统计图 课件(共52张PPT)2024-2025学年数学湘教版七年级下册
文档属性
| 名称 | 6.2.1 统计图 课件(共52张PPT)2024-2025学年数学湘教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 16:37:33 | ||
图片预览








文档简介
(共52张PPT)
6.2.1 统计图
我们知道,根据实际问题收集、整理数据后, 需要将数据以恰当的方式进行表示.
下面用来描述、分析数据的统计图,你认识几个?
条形统计图的概念
由两条互相垂直的数轴表示两个不同的项目,用一个单位长度表示一定的数量,根据数量的多少画成长短不同的小长方形,再把这些小长方形按照一定的顺序排列起来,制成条形统计图.
画条形统计图的步骤
(1)先观察所考察的对象的个数,以确定横轴的长度.
(2)以横轴、纵轴的最大长度确定单位长度,计算出每个对象的高度.
(3)取适当的长度画好横轴和纵轴,根据每个对象的实际数量,按适当的比例画出每个小长方形(即条形).
(4)标上单位名称和数量.
条形统计图的特点
利用条形统计图可以直观地表示事物的数量大小并进行比较.
缺点:不能准确地描述各部分量之间的关系以及各部分占总体的百分比的大小.
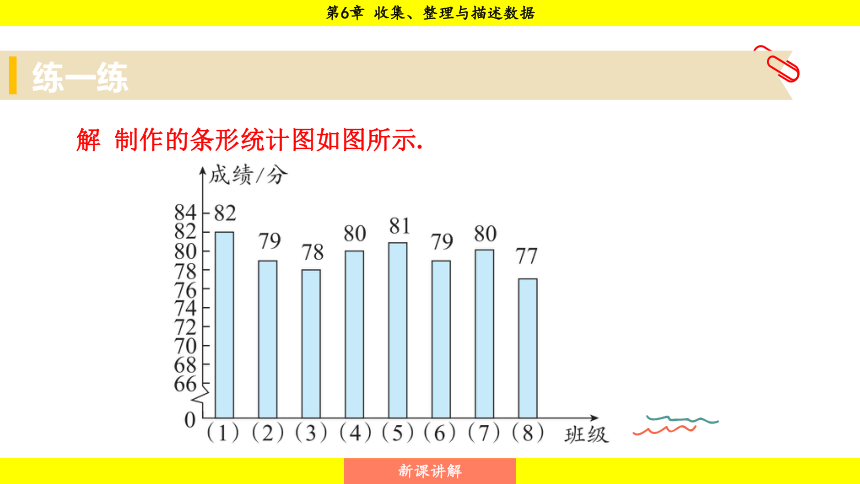
七年级(1)~(8)班期中考试的数学平均成绩如表所示.
请用条形统计图将表格中的数据表示出来.
解 制作的条形统计图如图所示.
条形统计图是通过条形的高度来表示数据的大小的,易于比较数据之间的差别.
如果要清楚地表示出每个项目的具体数目,那么应选择条形统计图.
注意:(1)纵轴表示数量,在箭头的顶端注明表示的项目的名称
及对应的单位.
(2)横轴表示类别,也要在箭头的顶端标注清楚.
折线统计图的概念
用一个单位长度表示一定的数量,根据数量的多少描出各点,然后用线段顺次把各点连接起来,这样的统计图叫折线统计图.
画折线统计图的步骤
(1)画两条互相垂直的数轴,横轴和纵轴分别表示不同的项目.
(2)描点,根据在横轴和纵轴上所对应的数确定点的位置.
(3)连线,把描出的点用线段连接起来.
折线统计图的特点
折线统计图表示事物随时间、地域或其他因素而变化的情况或趋势.
例2 为了提高长跑成绩,小彬坚持锻炼并于每周日记录下1500m跑步的成绩,如图所示。
根据从折线统计图上得到的信息,回答下列问题:
(1)小彬前三周的成绩均为 ,从第 周开始成绩逐渐变好.
(2)小彬第七周的成绩大致为多少?
8 min
四
小彬第七周的成绩大致为 5.5 min.
北京市生态环境局发布的数据显示,北京市2014—2022年全年空气质量优良的天数如下表所示,请根据下表,分别制作一个条形统计图和一个折线统计图.
为了直观地看出北京市2014—2022年全年空气质量优良天数的情况,可以画一个条形统计图来表示,如图所示.
为了清楚地表示北京市2014—2022年全年空气质量优良天数的变化趋势,可以画一个折线统计图来表示,如图所示.
(1)从条形统计图看出,北京市
2014—2022年全年空气质量优良天数的情况如何?
北京市2014—2022年全年空气质量优良天数越来越多.
(2)从折线统计图看出,北京市
2014—2022年全年空气质量优良天数的变化趋势如何?
与同学交流你的想法.
北京市2014—2022年全年空气质量优良天数呈增长趋势.交流略.
如果只需要表示北京市2022年全年
空气质量优良的天数占全年365天的百分比,
如何进行直观表示?
习惯上用圆和扇形来表示整体和部分的关系,即用圆表示整体,各个扇形的大小表示各部分所占的百分比.
扇形统计图的概念
用整个圆表示总体,用圆内每个扇形表示总体的一部分,各个扇形的大小表示各部分所占的百分比.这样的统计图叫作扇形统计图.
画扇形统计图的步骤
(1)计算每一部分数据占总体的百分比.
(2)计算各部分扇形的圆心角.
(3)在同一个圆中,根据计算
出的圆心角度数画出各个扇形,并且注明各部分的名称及其相应的百分比.
由于北京市2022年空气质量优良有286天,约占全年365天的78.4%.
又360°×78.4% ≈ 282°,
于是画一个圆,然后用量角器以圆心为顶点,
画角度为282°的扇形,并且在扇形内注明
78.4%,如图所示,
这样就直观地表示出了空气质量优良的天数占全年天数的百分比.
扇形统计图的特点
可以直观地看到我们考察的对象(总体)的组成部分、各部分在总体中所占的百分比.
1.扇形统计图一般不能直接从图中得到具体数量信息,我们用圆代表总数“1”,圆的大小与具体数量的大小无关.
2.扇形统计图一般以两种形式出现:一种是以百分比的形式出现,另外一种是以度数的形式出现.
例1 2022年8月17日,北京市政府正式批复了《北京市轨道交通线网规划(2020年—2035年)》,规划线网总规模约2683公里,包括区域快线(含市郊铁路)和城市轨道交通.其中区域快线总里程约1058公里,城市轨道交通总里程约1625公里.请根据上述信息,绘制扇形统计图.
解 第一步,计算区域快线总里程占规划线网总规模的百分比.
×100% ≈ 39.4%.
于是城市轨道交通总里程占规划线网总规模的百分比约为
1-39.4%=60.6%.
第二步,计算各部分扇形的圆心角.
360°×39.4%≈141.8°,
360°-141.8°=218.2°.
第三步,在同一个圆中,根据计算出的圆心角度数画出各个扇形,并且注明各部分的名称及其相应的百分比(如图).
例2 为了解某城市居民日常出行使用交通工具的情况,某研究机构用简单随机抽样方式进行调查,样本容量为602,调查结果统计如下:
请根据以上调查结果,制作扇形统计图,并在图中标出各出行方式的人数占总调查人数的百分比.
解 第一步,计算出该简单随机样本中各出行方式的人数占总调查人数的百分比.
第二步,计算各部分扇形的圆心角.
360°×41.2% ≈ 148.3°,
360°×45.7% ≈ 164.5°,
360°×11.6% ≈ 41.8°,
360°×1.5% = 5.4°.
第三步,在同一个圆中,根据计算出的圆心角度数画出各个扇形,并注明各部分的名称及其相应的百分比(如图).
为了解某市人口年龄结构情况,一机构对该市的人口数据进行随机抽样分析,绘制了如下尚不完整的统计表和统计图.
根据以上信息解答下列问题:
(1)m= ,扇形统计图中“C”对应的圆心角的度数是 ;
分析:根据“B”的人数和所占的百分比,可求出本次调查的总人数,用总人数减去其他类别的人数,求出“C”的人数,即m的值,再用360°乘“C”所占的百分比求出“C”对应的圆心角的度数.
1
18°
(2)该市现有人口约800万,请根据此次抽查结果,估计该市现有60岁及以上的人数.
×800=148(万).
答:该市现有60岁及以上的人数约为148万.
1.扇形统计图能够直观、生动地反映各部分占总体的百分比.
2.扇形的圆心角=360°×该部分占总体的百分比.
3.由于扇形统计图表明的是部分在总体中所占的百分比,因此一般不能直接从图中得到具体数量信息.
1 牛奶含有丰富的营养成分,下图是
某品牌牛奶的营养成分扇形统计图,每天
喝一袋250g的此品牌牛奶,能补充蛋白质多少克?
解:250×3.3%=8.25(g).
答:能补充蛋白质8.25g.
2 地球的表面积约为5.11亿平方千米,其中陆地面积约为1.49亿平方千米,海洋面积约为3.62亿平方千米.
请根据上述信息,绘制扇形统计图.
解:第一步,计算出海洋面积和陆地面积占地球表面积的百分比.
海洋面积占地球表面积的百分比:
×100% ≈ 70.8%,
陆地面积占地球表面积的百分比:
×100% ≈ 29.2%.
第二步,计算各部分扇形的圆心角.
360°×70.8% ≈ 255°,
360°×29.2% ≈ 105°.
第三步,在同一个圆中,根据计算出的圆心角度数画出各个扇形,并且注明各部分的名称及其相应的百分比,如图所示.
1.在植树节活动中,某单位组织职工开展植树竞赛,如图反映的是植树量与人数之间的关系.根据图中信息可知,参与本次活动的人数为( )
A. 19 B. 17
C. 14 D. 56
C
2.如图是某电商2024年1月至5月销售额
统计图,根据图中信息,可以判断相邻两个
月销售额变化最大的是( )
A. 1月至2月 B. 2月至3月
C. 3月至4月 D. 4月至5月
C
3.某校教师对该校学生的学习兴趣进行了一次抽样调查,把学生的学习兴趣分为三个层次,
A层次:很感兴趣,
B层次:较感兴趣,
C层次:不感兴趣,
并将调查结果绘制成了如图的统计图(不完整).
根据图中所给的信息,估计该校2400名学生中,
C层次的学生有 名.
360
4.要想了解某人心跳次数的变化情况,最好选用 统计图;
了解我国上届奥运会各项目获得的奖牌数占总奖牌数的情况,
最好选用 统计图.
折线
扇形
5.小明调查了某天气温的变化情况,结果如表:
请你根据上表绘制出合适的统计图反映这一天气温的变化趋势.
分析:要反映这一天气温的变化趋势,应选择折线统计图.
解 如图所示.
6.2.1 统计图
我们知道,根据实际问题收集、整理数据后, 需要将数据以恰当的方式进行表示.
下面用来描述、分析数据的统计图,你认识几个?
条形统计图的概念
由两条互相垂直的数轴表示两个不同的项目,用一个单位长度表示一定的数量,根据数量的多少画成长短不同的小长方形,再把这些小长方形按照一定的顺序排列起来,制成条形统计图.
画条形统计图的步骤
(1)先观察所考察的对象的个数,以确定横轴的长度.
(2)以横轴、纵轴的最大长度确定单位长度,计算出每个对象的高度.
(3)取适当的长度画好横轴和纵轴,根据每个对象的实际数量,按适当的比例画出每个小长方形(即条形).
(4)标上单位名称和数量.
条形统计图的特点
利用条形统计图可以直观地表示事物的数量大小并进行比较.
缺点:不能准确地描述各部分量之间的关系以及各部分占总体的百分比的大小.
七年级(1)~(8)班期中考试的数学平均成绩如表所示.
请用条形统计图将表格中的数据表示出来.
解 制作的条形统计图如图所示.
条形统计图是通过条形的高度来表示数据的大小的,易于比较数据之间的差别.
如果要清楚地表示出每个项目的具体数目,那么应选择条形统计图.
注意:(1)纵轴表示数量,在箭头的顶端注明表示的项目的名称
及对应的单位.
(2)横轴表示类别,也要在箭头的顶端标注清楚.
折线统计图的概念
用一个单位长度表示一定的数量,根据数量的多少描出各点,然后用线段顺次把各点连接起来,这样的统计图叫折线统计图.
画折线统计图的步骤
(1)画两条互相垂直的数轴,横轴和纵轴分别表示不同的项目.
(2)描点,根据在横轴和纵轴上所对应的数确定点的位置.
(3)连线,把描出的点用线段连接起来.
折线统计图的特点
折线统计图表示事物随时间、地域或其他因素而变化的情况或趋势.
例2 为了提高长跑成绩,小彬坚持锻炼并于每周日记录下1500m跑步的成绩,如图所示。
根据从折线统计图上得到的信息,回答下列问题:
(1)小彬前三周的成绩均为 ,从第 周开始成绩逐渐变好.
(2)小彬第七周的成绩大致为多少?
8 min
四
小彬第七周的成绩大致为 5.5 min.
北京市生态环境局发布的数据显示,北京市2014—2022年全年空气质量优良的天数如下表所示,请根据下表,分别制作一个条形统计图和一个折线统计图.
为了直观地看出北京市2014—2022年全年空气质量优良天数的情况,可以画一个条形统计图来表示,如图所示.
为了清楚地表示北京市2014—2022年全年空气质量优良天数的变化趋势,可以画一个折线统计图来表示,如图所示.
(1)从条形统计图看出,北京市
2014—2022年全年空气质量优良天数的情况如何?
北京市2014—2022年全年空气质量优良天数越来越多.
(2)从折线统计图看出,北京市
2014—2022年全年空气质量优良天数的变化趋势如何?
与同学交流你的想法.
北京市2014—2022年全年空气质量优良天数呈增长趋势.交流略.
如果只需要表示北京市2022年全年
空气质量优良的天数占全年365天的百分比,
如何进行直观表示?
习惯上用圆和扇形来表示整体和部分的关系,即用圆表示整体,各个扇形的大小表示各部分所占的百分比.
扇形统计图的概念
用整个圆表示总体,用圆内每个扇形表示总体的一部分,各个扇形的大小表示各部分所占的百分比.这样的统计图叫作扇形统计图.
画扇形统计图的步骤
(1)计算每一部分数据占总体的百分比.
(2)计算各部分扇形的圆心角.
(3)在同一个圆中,根据计算
出的圆心角度数画出各个扇形,并且注明各部分的名称及其相应的百分比.
由于北京市2022年空气质量优良有286天,约占全年365天的78.4%.
又360°×78.4% ≈ 282°,
于是画一个圆,然后用量角器以圆心为顶点,
画角度为282°的扇形,并且在扇形内注明
78.4%,如图所示,
这样就直观地表示出了空气质量优良的天数占全年天数的百分比.
扇形统计图的特点
可以直观地看到我们考察的对象(总体)的组成部分、各部分在总体中所占的百分比.
1.扇形统计图一般不能直接从图中得到具体数量信息,我们用圆代表总数“1”,圆的大小与具体数量的大小无关.
2.扇形统计图一般以两种形式出现:一种是以百分比的形式出现,另外一种是以度数的形式出现.
例1 2022年8月17日,北京市政府正式批复了《北京市轨道交通线网规划(2020年—2035年)》,规划线网总规模约2683公里,包括区域快线(含市郊铁路)和城市轨道交通.其中区域快线总里程约1058公里,城市轨道交通总里程约1625公里.请根据上述信息,绘制扇形统计图.
解 第一步,计算区域快线总里程占规划线网总规模的百分比.
×100% ≈ 39.4%.
于是城市轨道交通总里程占规划线网总规模的百分比约为
1-39.4%=60.6%.
第二步,计算各部分扇形的圆心角.
360°×39.4%≈141.8°,
360°-141.8°=218.2°.
第三步,在同一个圆中,根据计算出的圆心角度数画出各个扇形,并且注明各部分的名称及其相应的百分比(如图).
例2 为了解某城市居民日常出行使用交通工具的情况,某研究机构用简单随机抽样方式进行调查,样本容量为602,调查结果统计如下:
请根据以上调查结果,制作扇形统计图,并在图中标出各出行方式的人数占总调查人数的百分比.
解 第一步,计算出该简单随机样本中各出行方式的人数占总调查人数的百分比.
第二步,计算各部分扇形的圆心角.
360°×41.2% ≈ 148.3°,
360°×45.7% ≈ 164.5°,
360°×11.6% ≈ 41.8°,
360°×1.5% = 5.4°.
第三步,在同一个圆中,根据计算出的圆心角度数画出各个扇形,并注明各部分的名称及其相应的百分比(如图).
为了解某市人口年龄结构情况,一机构对该市的人口数据进行随机抽样分析,绘制了如下尚不完整的统计表和统计图.
根据以上信息解答下列问题:
(1)m= ,扇形统计图中“C”对应的圆心角的度数是 ;
分析:根据“B”的人数和所占的百分比,可求出本次调查的总人数,用总人数减去其他类别的人数,求出“C”的人数,即m的值,再用360°乘“C”所占的百分比求出“C”对应的圆心角的度数.
1
18°
(2)该市现有人口约800万,请根据此次抽查结果,估计该市现有60岁及以上的人数.
×800=148(万).
答:该市现有60岁及以上的人数约为148万.
1.扇形统计图能够直观、生动地反映各部分占总体的百分比.
2.扇形的圆心角=360°×该部分占总体的百分比.
3.由于扇形统计图表明的是部分在总体中所占的百分比,因此一般不能直接从图中得到具体数量信息.
1 牛奶含有丰富的营养成分,下图是
某品牌牛奶的营养成分扇形统计图,每天
喝一袋250g的此品牌牛奶,能补充蛋白质多少克?
解:250×3.3%=8.25(g).
答:能补充蛋白质8.25g.
2 地球的表面积约为5.11亿平方千米,其中陆地面积约为1.49亿平方千米,海洋面积约为3.62亿平方千米.
请根据上述信息,绘制扇形统计图.
解:第一步,计算出海洋面积和陆地面积占地球表面积的百分比.
海洋面积占地球表面积的百分比:
×100% ≈ 70.8%,
陆地面积占地球表面积的百分比:
×100% ≈ 29.2%.
第二步,计算各部分扇形的圆心角.
360°×70.8% ≈ 255°,
360°×29.2% ≈ 105°.
第三步,在同一个圆中,根据计算出的圆心角度数画出各个扇形,并且注明各部分的名称及其相应的百分比,如图所示.
1.在植树节活动中,某单位组织职工开展植树竞赛,如图反映的是植树量与人数之间的关系.根据图中信息可知,参与本次活动的人数为( )
A. 19 B. 17
C. 14 D. 56
C
2.如图是某电商2024年1月至5月销售额
统计图,根据图中信息,可以判断相邻两个
月销售额变化最大的是( )
A. 1月至2月 B. 2月至3月
C. 3月至4月 D. 4月至5月
C
3.某校教师对该校学生的学习兴趣进行了一次抽样调查,把学生的学习兴趣分为三个层次,
A层次:很感兴趣,
B层次:较感兴趣,
C层次:不感兴趣,
并将调查结果绘制成了如图的统计图(不完整).
根据图中所给的信息,估计该校2400名学生中,
C层次的学生有 名.
360
4.要想了解某人心跳次数的变化情况,最好选用 统计图;
了解我国上届奥运会各项目获得的奖牌数占总奖牌数的情况,
最好选用 统计图.
折线
扇形
5.小明调查了某天气温的变化情况,结果如表:
请你根据上表绘制出合适的统计图反映这一天气温的变化趋势.
分析:要反映这一天气温的变化趋势,应选择折线统计图.
解 如图所示.
同课章节目录
