2025北师大版数学七年级下册同步练习 第五章 问题解决策略转化(含答案)
文档属性
| 名称 | 2025北师大版数学七年级下册同步练习 第五章 问题解决策略转化(含答案) | 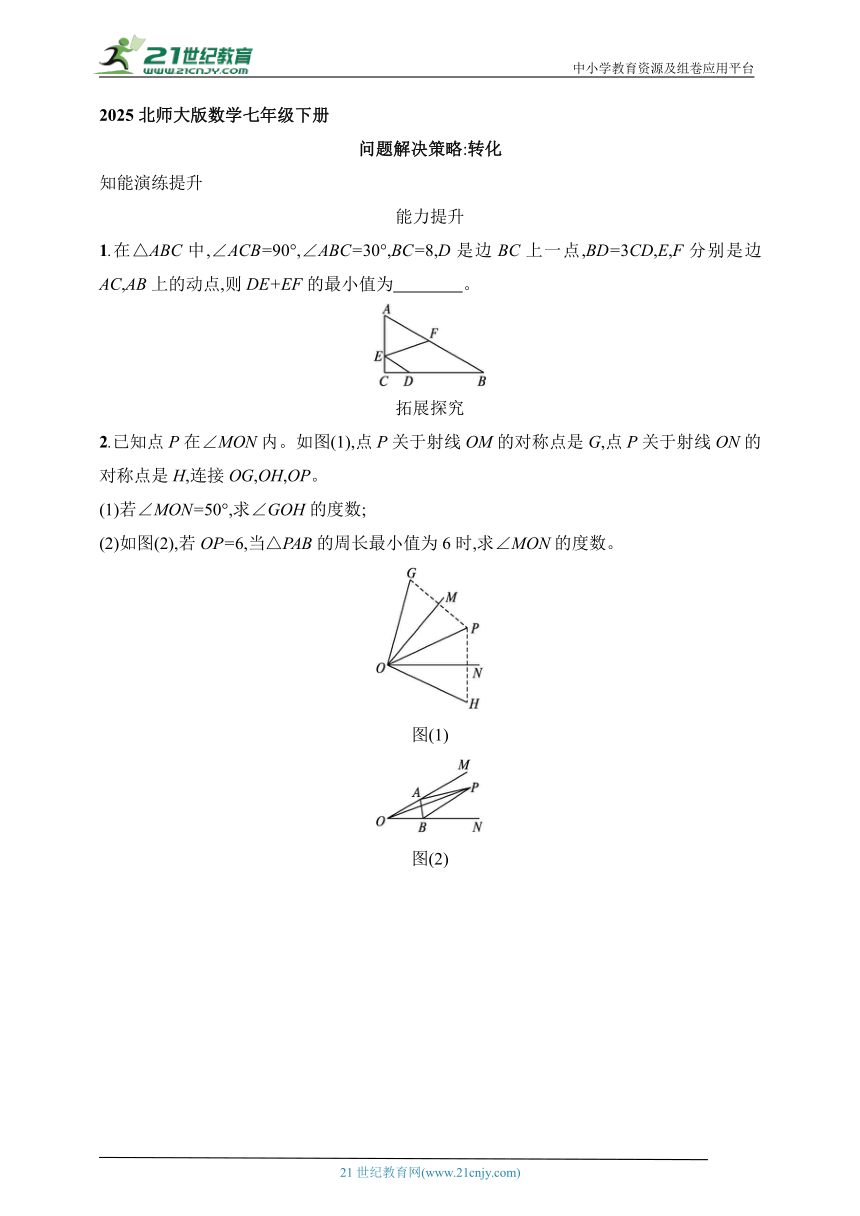 | |
| 格式 | docx | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 15:02:40 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025北师大版数学七年级下册
问题解决策略:转化
知能演练提升
能力提升
1.在△ABC中,∠ACB=90°,∠ABC=30°,BC=8,D是边BC上一点,BD=3CD,E,F分别是边AC,AB上的动点,则DE+EF的最小值为 。
拓展探究
2.已知点P在∠MON内。如图(1),点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG,OH,OP。
(1)若∠MON=50°,求∠GOH的度数;
(2)如图(2),若OP=6,当△PAB的周长最小值为6时,求∠MON的度数。
图(1)
图(2)
参考答案
知能演练·提升
能力提升
1.5
拓展探究
2.解 (1)因为点P关于射线OM的对称点是G,所以∠GOM=∠POM。
因为点P关于射线ON的对称点是H,
所以∠HON=∠PON。
因为∠MON=∠MOP+∠NOP=50°,
所以∠GOH=∠GOM+∠MOP+∠NOP+∠HON=2∠MON=100°。
(2)如图,作点P关于OM,ON的对称点P'和P″,连接P'P″,OP',OP″。
则PA=P'A,PB=P″B,OP'=OP,OP″=OP,∠P'OM=∠POM,∠PON=∠P″ON。
因为△PAB的周长最小值为6,OP=6,
所以P'P″=OP'=OP″=6,
所以△OP'P″为等边三角形,
所以∠P'OP″=60°。
因为∠P'OP″=∠P'OM+∠POM+∠PON+∠P″ON=2∠MON,
所以∠MON=30°。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师大版数学七年级下册
问题解决策略:转化
知能演练提升
能力提升
1.在△ABC中,∠ACB=90°,∠ABC=30°,BC=8,D是边BC上一点,BD=3CD,E,F分别是边AC,AB上的动点,则DE+EF的最小值为 。
拓展探究
2.已知点P在∠MON内。如图(1),点P关于射线OM的对称点是G,点P关于射线ON的对称点是H,连接OG,OH,OP。
(1)若∠MON=50°,求∠GOH的度数;
(2)如图(2),若OP=6,当△PAB的周长最小值为6时,求∠MON的度数。
图(1)
图(2)
参考答案
知能演练·提升
能力提升
1.5
拓展探究
2.解 (1)因为点P关于射线OM的对称点是G,所以∠GOM=∠POM。
因为点P关于射线ON的对称点是H,
所以∠HON=∠PON。
因为∠MON=∠MOP+∠NOP=50°,
所以∠GOH=∠GOM+∠MOP+∠NOP+∠HON=2∠MON=100°。
(2)如图,作点P关于OM,ON的对称点P'和P″,连接P'P″,OP',OP″。
则PA=P'A,PB=P″B,OP'=OP,OP″=OP,∠P'OM=∠POM,∠PON=∠P″ON。
因为△PAB的周长最小值为6,OP=6,
所以P'P″=OP'=OP″=6,
所以△OP'P″为等边三角形,
所以∠P'OP″=60°。
因为∠P'OP″=∠P'OM+∠POM+∠PON+∠P″ON=2∠MON,
所以∠MON=30°。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
