2025北师大版数学七年级下册同步练习 2.3 第2课时 平行线的性质与判定的综合运用(含答案)
文档属性
| 名称 | 2025北师大版数学七年级下册同步练习 2.3 第2课时 平行线的性质与判定的综合运用(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 340.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 15:38:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025北师大版数学七年级下册
第二课时 平行线的性质与判定的综合运用
知能演练提升
能力提升
1.(2024重庆渝北区期末)如图,点C在线段BF上,且CA平分∠DCB,AD∥BC,点E在AC上。若∠CBE=∠D,∠ABE∶∠ABC=1∶3,∠CAB=44°,则∠DAC的度数为 。
2.(2024重庆沙坪坝区校级开学)如图,已知点D是△ABC的边CB延长线上的一点,DE⊥AC于点E,点G是边AB上一点,∠AGF=∠ABC,∠BFG=∠D,试判断BF与AC的位置关系,并说明理由。
3.如图,AB∥CD,连接CA并延长至点H,CF平分∠ACD交AB于点F,CE⊥CF,∠GAH与∠AFC互余。
(1)试判断AG与CE的位置关系,并说明理由;
(2)若∠GAF=110°,求∠AFC的度数。
拓展探究
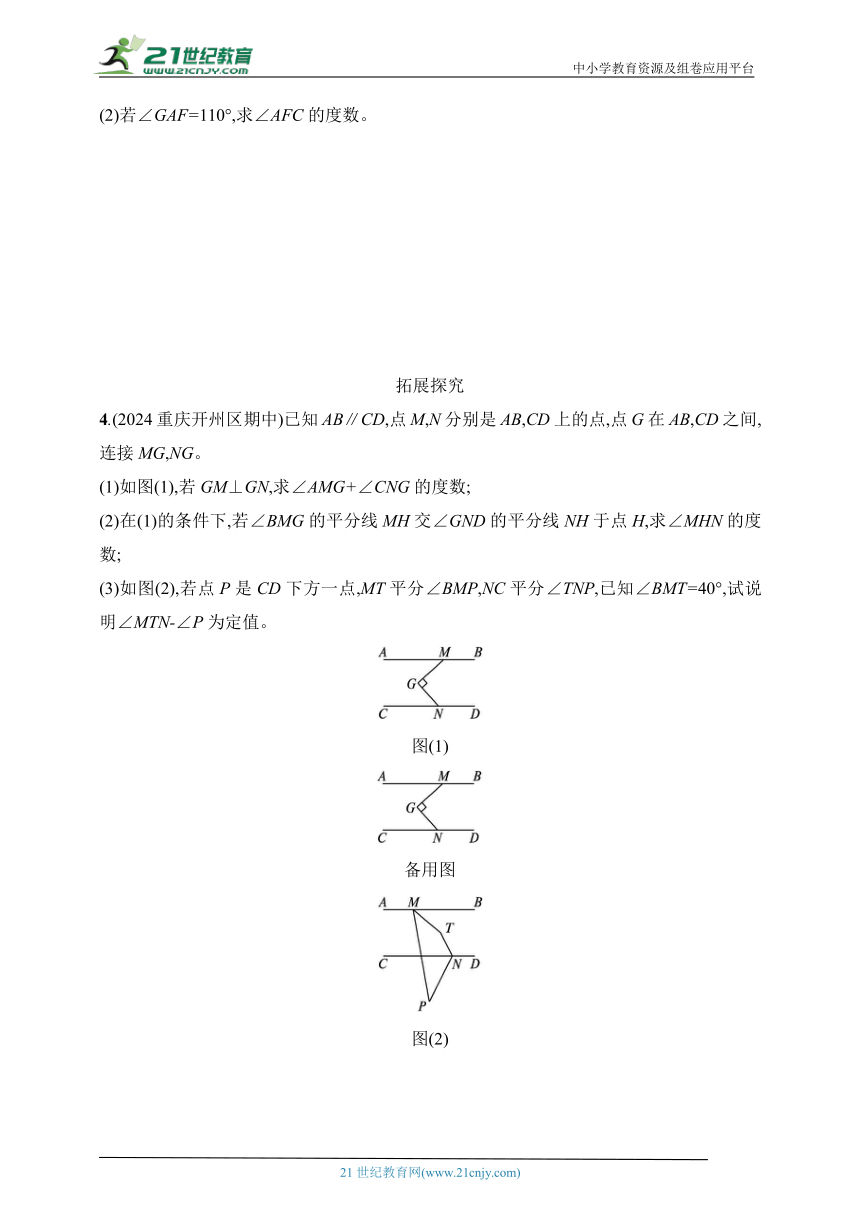
4.(2024重庆开州区期中)已知AB∥CD,点M,N分别是AB,CD上的点,点G在AB,CD之间,连接MG,NG。
(1)如图(1),若GM⊥GN,求∠AMG+∠CNG的度数;
(2)在(1)的条件下,若∠BMG的平分线MH交∠GND的平分线NH于点H,求∠MHN的度数;
(3)如图(2),若点P是CD下方一点,MT平分∠BMP,NC平分∠TNP,已知∠BMT=40°,试说明∠MTN-∠P为定值。
图(1)
备用图
图(2)
参考答案
知能演练·提升
能力提升
1.67°
2.解 BF⊥AC,理由如下:
因为∠AGF=∠ABC,
所以FG∥BC,
所以∠GFB=∠FBC。
因为∠GFB=∠D,
所以∠FBC=∠D,
所以BF∥DE。
因为DE⊥AC,
所以BF⊥AC。
3.解 (1)AG∥CE,理由如下:
因为AB∥CD,
所以∠AFC=∠DCF。
因为CF平分∠ACD,
所以∠FCD=∠ACF,
所以∠AFC=∠ACF。
又因为CE⊥CF,∠GAH与∠AFC互余,
所以∠ECH=∠GAH,
所以AG∥CE。
(2)因为AB∥CD,
所以∠HCD=∠HAF。
因为AG∥CE,
所以∠HCE=∠HAG,
所以∠ECD=∠GAF=110°。
又因为CE⊥CF,
所以∠DCF=∠ECD-∠ECF=20°,
所以∠AFC=∠DCF=20°。
拓展探究
4.解 (1)如图(1),过点G作GE∥AB,
图(1)
因为AB∥CD,
所以AB∥GE∥CD,
所以∠AMG=∠1,∠CNG=∠2。
因为GM⊥GN,
所以∠MGN=90°,
所以∠AMG+∠CNG=∠1+∠2=∠MGN=90°。
(2)如图(2),作∠BMG的平分线MH与∠GND的平分线NH交于点H,过点H作HF∥AB交GM于点F,
图(2)
因为∠AMG+∠CNG=90°,∠AMG+∠BMG=180°,∠CNG+∠GND=180°,
所以∠BMG+∠GND=360°-90°=270°。
因为MH平分∠BMG,NH平分∠GND,
所以∠3+∠6=(∠BMG+∠GND)=135°。
因为AB∥CD,
所以AB∥HF∥CD,
所以∠3=∠4,∠5=∠6,
所以∠MHN=∠4+∠5=∠3+∠6=135°。
(3)如图(3),将MP与CD的交点记作K,
图(3)
因为MT平分∠BMP,且∠BMT=40°,
所以∠1=∠2=40°,∠BMP=80°。
因为NC平分∠TNP,
所以∠3=∠4。
设∠3=∠4=x°,
所以∠TND=180°-x°。
由(1)可得∠MTN=∠1+∠TND=40°+180°-x°=220°-x°。
因为AB∥CD,
所以∠NKP=∠BMP=80°,
所以在△KPN中,∠P=180°-80°-x°=100°-x°,
所以∠MTN-∠P=120°,即∠MTN-∠P为定值。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师大版数学七年级下册
第二课时 平行线的性质与判定的综合运用
知能演练提升
能力提升
1.(2024重庆渝北区期末)如图,点C在线段BF上,且CA平分∠DCB,AD∥BC,点E在AC上。若∠CBE=∠D,∠ABE∶∠ABC=1∶3,∠CAB=44°,则∠DAC的度数为 。
2.(2024重庆沙坪坝区校级开学)如图,已知点D是△ABC的边CB延长线上的一点,DE⊥AC于点E,点G是边AB上一点,∠AGF=∠ABC,∠BFG=∠D,试判断BF与AC的位置关系,并说明理由。
3.如图,AB∥CD,连接CA并延长至点H,CF平分∠ACD交AB于点F,CE⊥CF,∠GAH与∠AFC互余。
(1)试判断AG与CE的位置关系,并说明理由;
(2)若∠GAF=110°,求∠AFC的度数。
拓展探究
4.(2024重庆开州区期中)已知AB∥CD,点M,N分别是AB,CD上的点,点G在AB,CD之间,连接MG,NG。
(1)如图(1),若GM⊥GN,求∠AMG+∠CNG的度数;
(2)在(1)的条件下,若∠BMG的平分线MH交∠GND的平分线NH于点H,求∠MHN的度数;
(3)如图(2),若点P是CD下方一点,MT平分∠BMP,NC平分∠TNP,已知∠BMT=40°,试说明∠MTN-∠P为定值。
图(1)
备用图
图(2)
参考答案
知能演练·提升
能力提升
1.67°
2.解 BF⊥AC,理由如下:
因为∠AGF=∠ABC,
所以FG∥BC,
所以∠GFB=∠FBC。
因为∠GFB=∠D,
所以∠FBC=∠D,
所以BF∥DE。
因为DE⊥AC,
所以BF⊥AC。
3.解 (1)AG∥CE,理由如下:
因为AB∥CD,
所以∠AFC=∠DCF。
因为CF平分∠ACD,
所以∠FCD=∠ACF,
所以∠AFC=∠ACF。
又因为CE⊥CF,∠GAH与∠AFC互余,
所以∠ECH=∠GAH,
所以AG∥CE。
(2)因为AB∥CD,
所以∠HCD=∠HAF。
因为AG∥CE,
所以∠HCE=∠HAG,
所以∠ECD=∠GAF=110°。
又因为CE⊥CF,
所以∠DCF=∠ECD-∠ECF=20°,
所以∠AFC=∠DCF=20°。
拓展探究
4.解 (1)如图(1),过点G作GE∥AB,
图(1)
因为AB∥CD,
所以AB∥GE∥CD,
所以∠AMG=∠1,∠CNG=∠2。
因为GM⊥GN,
所以∠MGN=90°,
所以∠AMG+∠CNG=∠1+∠2=∠MGN=90°。
(2)如图(2),作∠BMG的平分线MH与∠GND的平分线NH交于点H,过点H作HF∥AB交GM于点F,
图(2)
因为∠AMG+∠CNG=90°,∠AMG+∠BMG=180°,∠CNG+∠GND=180°,
所以∠BMG+∠GND=360°-90°=270°。
因为MH平分∠BMG,NH平分∠GND,
所以∠3+∠6=(∠BMG+∠GND)=135°。
因为AB∥CD,
所以AB∥HF∥CD,
所以∠3=∠4,∠5=∠6,
所以∠MHN=∠4+∠5=∠3+∠6=135°。
(3)如图(3),将MP与CD的交点记作K,
图(3)
因为MT平分∠BMP,且∠BMT=40°,
所以∠1=∠2=40°,∠BMP=80°。
因为NC平分∠TNP,
所以∠3=∠4。
设∠3=∠4=x°,
所以∠TND=180°-x°。
由(1)可得∠MTN=∠1+∠TND=40°+180°-x°=220°-x°。
因为AB∥CD,
所以∠NKP=∠BMP=80°,
所以在△KPN中,∠P=180°-80°-x°=100°-x°,
所以∠MTN-∠P=120°,即∠MTN-∠P为定值。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
