2025人教版数学七年级下册同步练习 期中综合训练(含答案)
文档属性
| 名称 | 2025人教版数学七年级下册同步练习 期中综合训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 535.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 16:44:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025人教版数学七年级下册
期中综合训练
一、选择题(在每小题给出的四个选项中,只有一项是符合要求的)
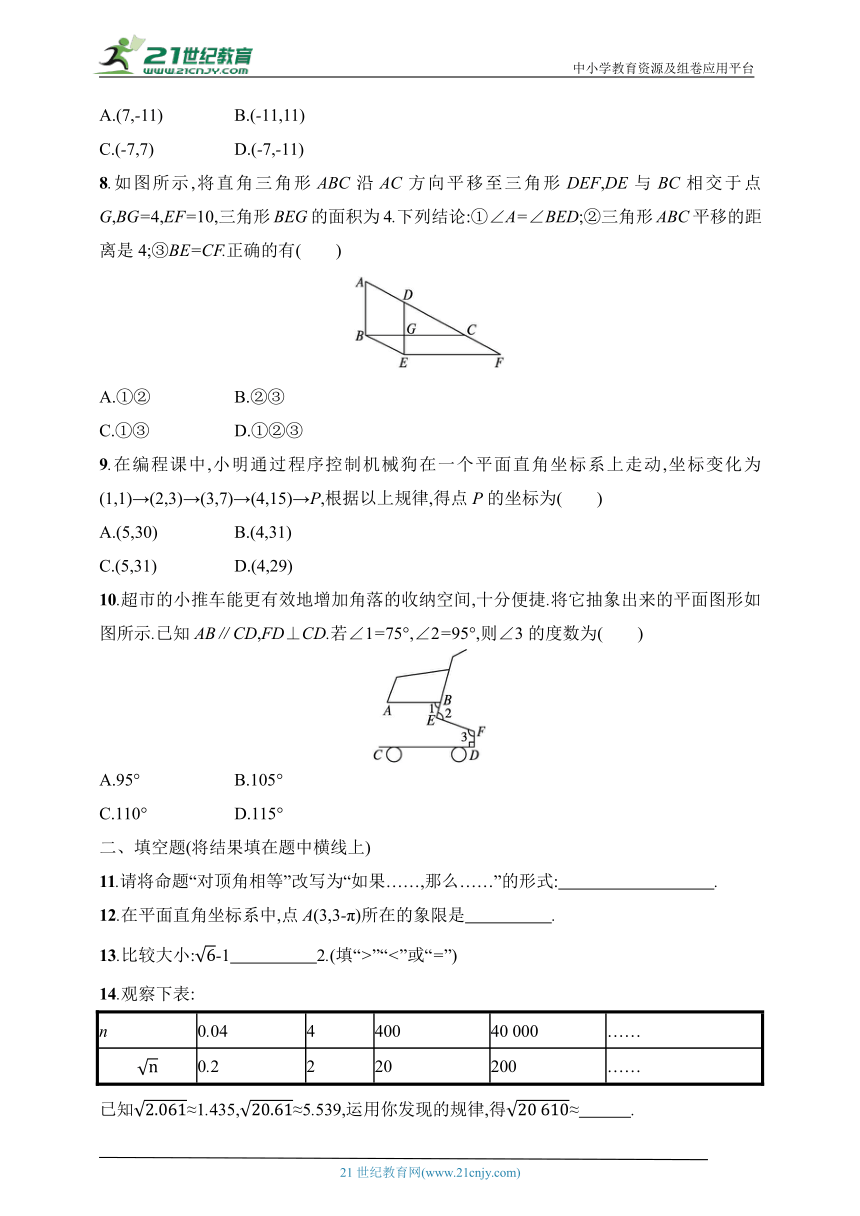
1.下列图案中的阴影部分可以由图案中的一部分平移得到的是( )
2.下列各点在x轴负半轴上的是( )
A.(2,0) B.(-2,0)
C.(0,2) D.(0,-2)
3.在下列四个数中:-,0,,0.101 001,属于无理数的是( )
A.- B.0
C. D.0.101 001
4.学完平方根后,老师布置了4道填空题,下面是嘉嘉的完成情况:
①0的平方根是0;②16的平方根是±4;③9的算术平方根是3;④的平方根是±5.嘉嘉做对了几道题( )
A.1道 B.2道
C.3道 D.4道
5.定义新运算:规定a*b=a+2ab2(b≥0),则2*4=( )
A.32 B.36
C.68 D.64
6.如图所示,直线AB,CD相交于点O.若∠1=40°,∠2=120°,则∠COM的度数为( )
A.70° B.80°
C.90° D.100°
7.在平面直角坐标系中,点A的坐标是(-7,11),则点A与下列哪个点组成的直线与x轴平行( )
A.(7,-11) B.(-11,11)
C.(-7,7) D.(-7,-11)
8.如图所示,将直角三角形ABC沿AC方向平移至三角形DEF,DE与BC相交于点G,BG=4,EF=10,三角形BEG的面积为4.下列结论:①∠A=∠BED;②三角形ABC平移的距离是4;③BE=CF.正确的有( )
A.①② B.②③
C.①③ D.①②③
9.在编程课中,小明通过程序控制机械狗在一个平面直角坐标系上走动,坐标变化为(1,1)→(2,3)→(3,7)→(4,15)→P,根据以上规律,得点P的坐标为( )
A.(5,30) B.(4,31)
C.(5,31) D.(4,29)
10.超市的小推车能更有效地增加角落的收纳空间,十分便捷.将它抽象出来的平面图形如图所示.已知AB∥CD,FD⊥CD.若∠1=75°,∠2=95°,则∠3的度数为( )
A.95° B.105°
C.110° D.115°
二、填空题(将结果填在题中横线上)
11.请将命题“对顶角相等”改写为“如果……,那么……”的形式: .
12.在平面直角坐标系中,点A(3,3-π)所在的象限是 .
13.比较大小:-1 2.(填“>”“<”或“=”)
14.观察下表:
n 0.04 4 400 40 000 ……
0.2 2 20 200 ……
已知≈1.435,≈5.539,运用你发现的规律,得≈ .
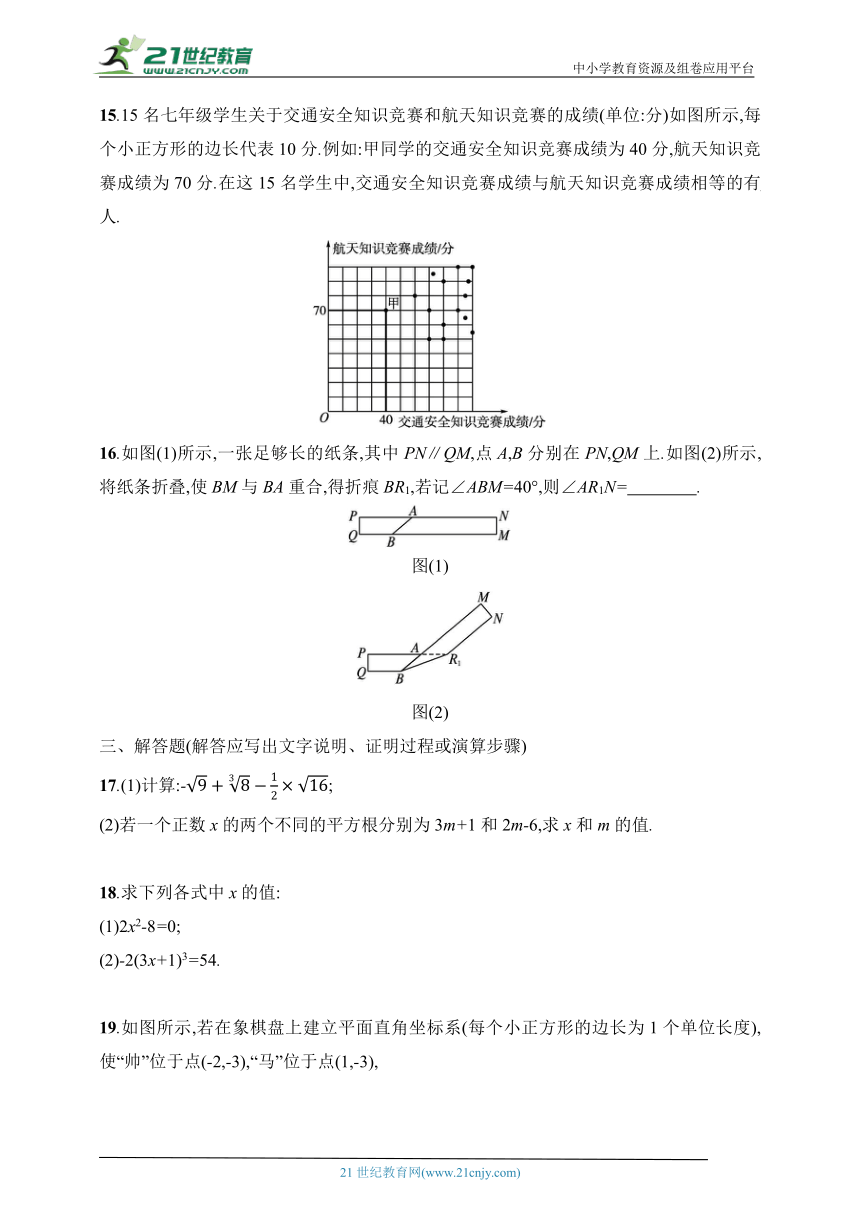
15.15名七年级学生关于交通安全知识竞赛和航天知识竞赛的成绩(单位:分)如图所示,每个小正方形的边长代表10分.例如:甲同学的交通安全知识竞赛成绩为40分,航天知识竞赛成绩为70分.在这15名学生中,交通安全知识竞赛成绩与航天知识竞赛成绩相等的有 人.
16.如图(1)所示,一张足够长的纸条,其中PN∥QM,点A,B分别在PN,QM上.如图(2)所示,将纸条折叠,使BM与BA重合,得折痕BR1,若记∠ABM=40°,则∠AR1N= .
图(1)
图(2)
三、解答题(解答应写出文字说明、证明过程或演算步骤)
17.(1)计算:-;
(2)若一个正数x的两个不同的平方根分别为3m+1和2m-6,求x和m的值.
18.求下列各式中x的值:
(1)2x2-8=0;
(2)-2(3x+1)3=54.
19.如图所示,若在象棋盘上建立平面直角坐标系(每个小正方形的边长为1个单位长度),使“帅”位于点(-2,-3),“马”位于点(1,-3),
(1)画出所建立的平面直角坐标系;
(2)分别写出“兵”和“炮”两点在你所建立的平面直角坐标系中的坐标.
20.如图所示,已知直线AB∥CD,点E,G在直线AB上,点F在直线CD上,FE平分∠GFD,∠1=50°,求∠BEF的度数.
解:因为AB∥CD(已知),
所以∠1=∠2( ).
因为∠1=50°(已知),
所以∠2=50°(等式性质).
因为∠2+∠GFD=180°( ),
所以∠GFD= °.
(下面补充完整求∠BEF的度数的解题过程)
21.在平面直角坐标系中,已知点A(1,3),B(2,1),C(4,4),其中点A的位置如图所示.
(1)在图中建立平面直角坐标系,并画出三角形ABC;
(2)平移三角形ABC,使点A的对应点A'落在y轴上,点B的对应点B'落在x轴上,求此时点C的对应点C'的坐标.
22.在平面直角坐标系中,点P的横、纵坐标分别为x,y,已知(x-1)2=1,(y+1)3=27.
(1)求点P(x,y)的坐标;
(2)若点P在坐标轴上,点Q是第二象限内的点,PQ∥x轴,且PQ=3,求出点Q的坐标.
23.在平面直角坐标系中,已知点P(2m-7,n-6)在第四象限,且点P到x轴和y轴的距离分别为3和1.
(1)求m+n的平方根;
(2)设4m+3n+2的立方根为t,在同一个平面直角坐标系中还有一点Q,点Q(t,t2-2),请指出点Q是怎样由点P平移得到的
24.如图所示,已知直线a∥b,直线c分别和直线a,b相交于点C,D.
(1)∠1,∠2,∠3有怎样的数量关系 说明你的理由.
(2)如果点M在C,D之间运动,这种关系是否会发生变化 (直接写出结果,不需说明理由)
答案:
1.C
2.B 解析:在x轴负半轴上的点的横坐标是负数,纵坐标是0.观察各选项,只有B选项符合.故选B.
3.C
4.C 解析:①0的平方根是0,正确;
②16的平方根是±4,正确;
③9的算术平方根是3,正确;
④=5,其平方根是±,则④错误.故选C.
5.C 解析:由题意得,2*4=2+2×2×42=2×2+2×2×16=68.故选C.
6.B 解析:∵∠2=∠BOC=∠COM+∠1,∴∠COM=∠2-∠1=120°-40°=80°.故选B.
7.B 解析:因为点A的坐标是(-7,11),与点A组成的直线与x轴平行,所以该点的纵坐标为11.故选B.
8.C 解析:①因为直角三角形ABC沿AC方向平移至三角形DEF,
所以AB∥DE,AC∥BE.
所以∠A=∠GDC,∠BED=∠GDC.
所以∠A=∠BED,故①正确,符合题意;
②三角形ABC平移的距离是BE的长度,由BE>BG,可知BE>4,
所以三角形ABC平移的距离大于4,故②错误,不符合题意;
③由平移前后的对应点的连线平行且相等,可知BE=CF,故③正确,符合题意.
故选C.
9.C 解析:由(1,1)→(2,3)→(3,7)→(4,15),发现规律:横坐标都加1,纵坐标分别为21-1,22-1,23-1,24-1.所以点P的坐标为(5,25-1),即为(5,31).故选C.
10.C 解析:如图所示,过点E和点F分别作EG∥AB,FH∥AB,
∵AB∥EG∥FH,
∴∠BEG=∠1=75°.
∴∠FEG=∠2-∠BEG=95°-75°=20°.
∴∠HFE=∠FEG=20°.
∵AB∥CD,∴FH∥CD.
∵FD⊥CD,∴∠CDF=90°.
∴∠HFD=180°-∠CDF=90°.
∴∠3=∠HFE+∠HFD=20°+90°=110°.
故选C.
11.如果两个角是对顶角,那么这两个角相等
12.第四象限 解析:因为点A(3,3-π)的横坐标为正,纵坐标为负,所以点A(3,3-π)所在的象限是第四象限.
13.< 解析:∵4<6<9,
∴.
∴2<<3.
∴1<-1<2.
14.143.5
15.2 解析:因为题图中横、纵坐标相同的点有(70,70),(100,100),
所以交通安全知识竞赛成绩与航天知识竞赛成绩相等的有2人.
16.140° 解析:如题图(1)所示,
∵PN∥QM,
∴∠PAB=∠ABM=40°.
∴在题图(2)中,∠MAR1=∠PAB=40°.
∵AM∥R1N,
∴∠AR1N=180°-∠MAR1=180°-40°=140°.
故答案为140°.
17.解:(1)原式=-3+2-×4
=-3+2-2
=-3.
(2)由题意得,3m+1+2m-6=0.
解得m=1.
3m+1=4.
x=4×4=16.
18.解:(1)2x2-8=0.
x2=4.
x=2或x=-2.
(2)(3x+1)3=-27.
3x+1=-3.
3x=-4.
x=-.
19.解:(1)由题意,建立平面直角坐标系,如图所示.
(2)如(1)中图所示,“兵”和“炮”两点的坐标是:兵(-4,0),炮(-1,-1).
20.解:两直线平行,同位角相等 平角的定义 130
补充解答过程:
因为FE平分∠GFD,
所以∠3=∠GFD=×130°=65°.
因为AB∥CD,
所以∠BEF=180°-∠3=180°-65°=115°.
21.解:(1)如图所示,平面直角坐标系和三角形ABC即为所作.
(2)如图所示,三角形A'B'C'即为所作.
点C'的坐标为(3,3).
22.解:(1)∵(x-1)2=1,(y+1)3=27,
∴x-1=±1,y+1=3.
∴x=0或x=2,y=2.
∴点P的坐标为(0,2)或(2,2).
(2)∵点P在坐标轴上,
∴点P的坐标为(0,2).
∵Q是第二象限内的点,PQ∥x轴,且PQ=3,
∴点Q的坐标为(-3,2).
23.解:(1)因为点P(2m-7,n-6)在第四象限,且点P到x轴和y轴的距离分别为3和1,
所以点P的坐标为P(1,-3).
所以2m-7=1,n-6=-3,解得m=4,n=3.
所以m+n的平方根为±=±.
(2)当m=4,n=3时,4m+3n+2=4×4+3×3+2=27,
所以4m+3n+2的立方根t==3.
当t=3时,t2-2=9-2=7.
所以Q(3,7).
所以点Q是由点P(1,-3)向右平移2个单位长度,向上平移10个单位长度得到的.
24.解:(1)∠2=∠1+∠3.理由如下:
如图所示,过点M作MN∥a.
∵a∥b,
∴MN∥a∥b.
∴∠1=∠AMN,∠3=∠BMN.
∵∠2=∠AMN+∠BMN,
∴∠2=∠1+∠3.
(2)如果点M在点C和点D之间运动,这种关系不会发生变化.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教版数学七年级下册
期中综合训练
一、选择题(在每小题给出的四个选项中,只有一项是符合要求的)
1.下列图案中的阴影部分可以由图案中的一部分平移得到的是( )
2.下列各点在x轴负半轴上的是( )
A.(2,0) B.(-2,0)
C.(0,2) D.(0,-2)
3.在下列四个数中:-,0,,0.101 001,属于无理数的是( )
A.- B.0
C. D.0.101 001
4.学完平方根后,老师布置了4道填空题,下面是嘉嘉的完成情况:
①0的平方根是0;②16的平方根是±4;③9的算术平方根是3;④的平方根是±5.嘉嘉做对了几道题( )
A.1道 B.2道
C.3道 D.4道
5.定义新运算:规定a*b=a+2ab2(b≥0),则2*4=( )
A.32 B.36
C.68 D.64
6.如图所示,直线AB,CD相交于点O.若∠1=40°,∠2=120°,则∠COM的度数为( )
A.70° B.80°
C.90° D.100°
7.在平面直角坐标系中,点A的坐标是(-7,11),则点A与下列哪个点组成的直线与x轴平行( )
A.(7,-11) B.(-11,11)
C.(-7,7) D.(-7,-11)
8.如图所示,将直角三角形ABC沿AC方向平移至三角形DEF,DE与BC相交于点G,BG=4,EF=10,三角形BEG的面积为4.下列结论:①∠A=∠BED;②三角形ABC平移的距离是4;③BE=CF.正确的有( )
A.①② B.②③
C.①③ D.①②③
9.在编程课中,小明通过程序控制机械狗在一个平面直角坐标系上走动,坐标变化为(1,1)→(2,3)→(3,7)→(4,15)→P,根据以上规律,得点P的坐标为( )
A.(5,30) B.(4,31)
C.(5,31) D.(4,29)
10.超市的小推车能更有效地增加角落的收纳空间,十分便捷.将它抽象出来的平面图形如图所示.已知AB∥CD,FD⊥CD.若∠1=75°,∠2=95°,则∠3的度数为( )
A.95° B.105°
C.110° D.115°
二、填空题(将结果填在题中横线上)
11.请将命题“对顶角相等”改写为“如果……,那么……”的形式: .
12.在平面直角坐标系中,点A(3,3-π)所在的象限是 .
13.比较大小:-1 2.(填“>”“<”或“=”)
14.观察下表:
n 0.04 4 400 40 000 ……
0.2 2 20 200 ……
已知≈1.435,≈5.539,运用你发现的规律,得≈ .
15.15名七年级学生关于交通安全知识竞赛和航天知识竞赛的成绩(单位:分)如图所示,每个小正方形的边长代表10分.例如:甲同学的交通安全知识竞赛成绩为40分,航天知识竞赛成绩为70分.在这15名学生中,交通安全知识竞赛成绩与航天知识竞赛成绩相等的有 人.
16.如图(1)所示,一张足够长的纸条,其中PN∥QM,点A,B分别在PN,QM上.如图(2)所示,将纸条折叠,使BM与BA重合,得折痕BR1,若记∠ABM=40°,则∠AR1N= .
图(1)
图(2)
三、解答题(解答应写出文字说明、证明过程或演算步骤)
17.(1)计算:-;
(2)若一个正数x的两个不同的平方根分别为3m+1和2m-6,求x和m的值.
18.求下列各式中x的值:
(1)2x2-8=0;
(2)-2(3x+1)3=54.
19.如图所示,若在象棋盘上建立平面直角坐标系(每个小正方形的边长为1个单位长度),使“帅”位于点(-2,-3),“马”位于点(1,-3),
(1)画出所建立的平面直角坐标系;
(2)分别写出“兵”和“炮”两点在你所建立的平面直角坐标系中的坐标.
20.如图所示,已知直线AB∥CD,点E,G在直线AB上,点F在直线CD上,FE平分∠GFD,∠1=50°,求∠BEF的度数.
解:因为AB∥CD(已知),
所以∠1=∠2( ).
因为∠1=50°(已知),
所以∠2=50°(等式性质).
因为∠2+∠GFD=180°( ),
所以∠GFD= °.
(下面补充完整求∠BEF的度数的解题过程)
21.在平面直角坐标系中,已知点A(1,3),B(2,1),C(4,4),其中点A的位置如图所示.
(1)在图中建立平面直角坐标系,并画出三角形ABC;
(2)平移三角形ABC,使点A的对应点A'落在y轴上,点B的对应点B'落在x轴上,求此时点C的对应点C'的坐标.
22.在平面直角坐标系中,点P的横、纵坐标分别为x,y,已知(x-1)2=1,(y+1)3=27.
(1)求点P(x,y)的坐标;
(2)若点P在坐标轴上,点Q是第二象限内的点,PQ∥x轴,且PQ=3,求出点Q的坐标.
23.在平面直角坐标系中,已知点P(2m-7,n-6)在第四象限,且点P到x轴和y轴的距离分别为3和1.
(1)求m+n的平方根;
(2)设4m+3n+2的立方根为t,在同一个平面直角坐标系中还有一点Q,点Q(t,t2-2),请指出点Q是怎样由点P平移得到的
24.如图所示,已知直线a∥b,直线c分别和直线a,b相交于点C,D.
(1)∠1,∠2,∠3有怎样的数量关系 说明你的理由.
(2)如果点M在C,D之间运动,这种关系是否会发生变化 (直接写出结果,不需说明理由)
答案:
1.C
2.B 解析:在x轴负半轴上的点的横坐标是负数,纵坐标是0.观察各选项,只有B选项符合.故选B.
3.C
4.C 解析:①0的平方根是0,正确;
②16的平方根是±4,正确;
③9的算术平方根是3,正确;
④=5,其平方根是±,则④错误.故选C.
5.C 解析:由题意得,2*4=2+2×2×42=2×2+2×2×16=68.故选C.
6.B 解析:∵∠2=∠BOC=∠COM+∠1,∴∠COM=∠2-∠1=120°-40°=80°.故选B.
7.B 解析:因为点A的坐标是(-7,11),与点A组成的直线与x轴平行,所以该点的纵坐标为11.故选B.
8.C 解析:①因为直角三角形ABC沿AC方向平移至三角形DEF,
所以AB∥DE,AC∥BE.
所以∠A=∠GDC,∠BED=∠GDC.
所以∠A=∠BED,故①正确,符合题意;
②三角形ABC平移的距离是BE的长度,由BE>BG,可知BE>4,
所以三角形ABC平移的距离大于4,故②错误,不符合题意;
③由平移前后的对应点的连线平行且相等,可知BE=CF,故③正确,符合题意.
故选C.
9.C 解析:由(1,1)→(2,3)→(3,7)→(4,15),发现规律:横坐标都加1,纵坐标分别为21-1,22-1,23-1,24-1.所以点P的坐标为(5,25-1),即为(5,31).故选C.
10.C 解析:如图所示,过点E和点F分别作EG∥AB,FH∥AB,
∵AB∥EG∥FH,
∴∠BEG=∠1=75°.
∴∠FEG=∠2-∠BEG=95°-75°=20°.
∴∠HFE=∠FEG=20°.
∵AB∥CD,∴FH∥CD.
∵FD⊥CD,∴∠CDF=90°.
∴∠HFD=180°-∠CDF=90°.
∴∠3=∠HFE+∠HFD=20°+90°=110°.
故选C.
11.如果两个角是对顶角,那么这两个角相等
12.第四象限 解析:因为点A(3,3-π)的横坐标为正,纵坐标为负,所以点A(3,3-π)所在的象限是第四象限.
13.< 解析:∵4<6<9,
∴.
∴2<<3.
∴1<-1<2.
14.143.5
15.2 解析:因为题图中横、纵坐标相同的点有(70,70),(100,100),
所以交通安全知识竞赛成绩与航天知识竞赛成绩相等的有2人.
16.140° 解析:如题图(1)所示,
∵PN∥QM,
∴∠PAB=∠ABM=40°.
∴在题图(2)中,∠MAR1=∠PAB=40°.
∵AM∥R1N,
∴∠AR1N=180°-∠MAR1=180°-40°=140°.
故答案为140°.
17.解:(1)原式=-3+2-×4
=-3+2-2
=-3.
(2)由题意得,3m+1+2m-6=0.
解得m=1.
3m+1=4.
x=4×4=16.
18.解:(1)2x2-8=0.
x2=4.
x=2或x=-2.
(2)(3x+1)3=-27.
3x+1=-3.
3x=-4.
x=-.
19.解:(1)由题意,建立平面直角坐标系,如图所示.
(2)如(1)中图所示,“兵”和“炮”两点的坐标是:兵(-4,0),炮(-1,-1).
20.解:两直线平行,同位角相等 平角的定义 130
补充解答过程:
因为FE平分∠GFD,
所以∠3=∠GFD=×130°=65°.
因为AB∥CD,
所以∠BEF=180°-∠3=180°-65°=115°.
21.解:(1)如图所示,平面直角坐标系和三角形ABC即为所作.
(2)如图所示,三角形A'B'C'即为所作.
点C'的坐标为(3,3).
22.解:(1)∵(x-1)2=1,(y+1)3=27,
∴x-1=±1,y+1=3.
∴x=0或x=2,y=2.
∴点P的坐标为(0,2)或(2,2).
(2)∵点P在坐标轴上,
∴点P的坐标为(0,2).
∵Q是第二象限内的点,PQ∥x轴,且PQ=3,
∴点Q的坐标为(-3,2).
23.解:(1)因为点P(2m-7,n-6)在第四象限,且点P到x轴和y轴的距离分别为3和1,
所以点P的坐标为P(1,-3).
所以2m-7=1,n-6=-3,解得m=4,n=3.
所以m+n的平方根为±=±.
(2)当m=4,n=3时,4m+3n+2=4×4+3×3+2=27,
所以4m+3n+2的立方根t==3.
当t=3时,t2-2=9-2=7.
所以Q(3,7).
所以点Q是由点P(1,-3)向右平移2个单位长度,向上平移10个单位长度得到的.
24.解:(1)∠2=∠1+∠3.理由如下:
如图所示,过点M作MN∥a.
∵a∥b,
∴MN∥a∥b.
∴∠1=∠AMN,∠3=∠BMN.
∵∠2=∠AMN+∠BMN,
∴∠2=∠1+∠3.
(2)如果点M在点C和点D之间运动,这种关系不会发生变化.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
