华师大版(2024)数学七下5.2.2解一元一次方程(第3课时) 同步教学课件(共30张PPT)
文档属性
| 名称 | 华师大版(2024)数学七下5.2.2解一元一次方程(第3课时) 同步教学课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 09:54:14 | ||
图片预览







文档简介
(共30张PPT)
(华师大版)七年级
下
5.2.2解一元一次方程(第3课时)
一元一次方程
第5章
“五”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.能根据具体问题中的等量关系准确列出方程;
2.进一步体会建模思想,并能检验结果是否合理.
新知导入
48位大学生暑假到水利工地做义工,若每人每天平均挖土5 m3或运土3 m3,他们如何配合,才能使挖出的土及时运走?
若设其中x人挖土,则运土的人数为 人,根据题意,可列方程 .
(48-x)
5x=3(48-x)
新知讲解
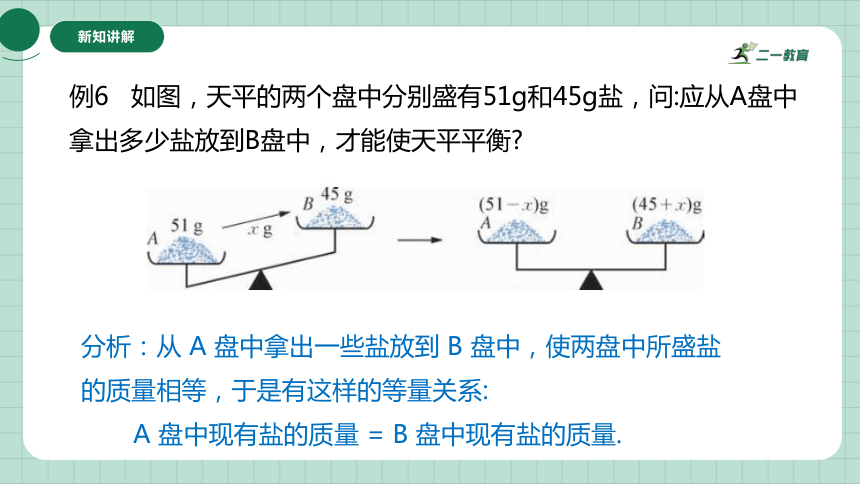
例6 如图,天平的两个盘中分别盛有51g和45g盐,问:应从A盘中拿出多少盐放到B盘中,才能使天平平衡
分析:从 A 盘中拿出一些盐放到 B 盘中,使两盘中所盛盐的质量相等,于是有这样的等量关系:
A 盘中现有盐的质量 = B 盘中现有盐的质量.
新知讲解
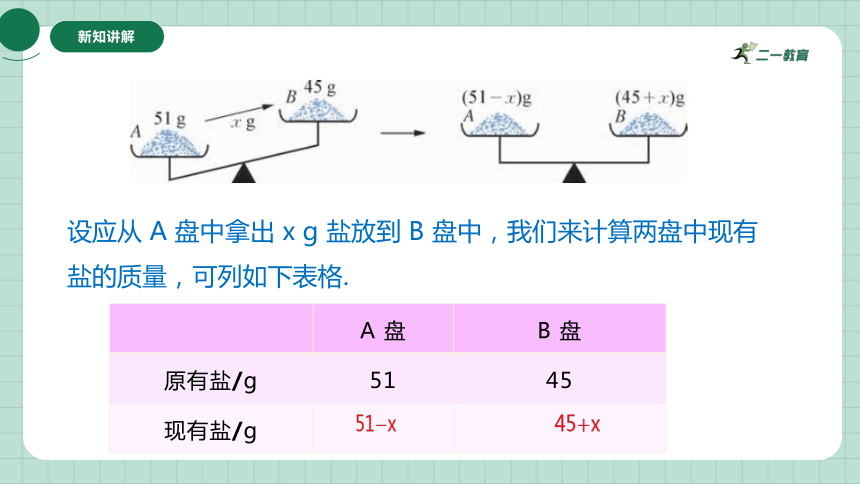
设应从 A 盘中拿出 x g 盐放到 B 盘中,我们来计算两盘中现有盐的质量,可列如下表格.
A 盘 B 盘
原有盐/g 51 45
现有盐/g
51x
45x
新知讲解
解:设应从 A 盘中拿出 x g 盐放到 B 盘中,则根据题意,得
51x=45x.
解这个方程,得
x=3.
经检验,符合题意.
答:应从 A 盘中拿出 3 g 盐放到 B 盘中,才能使天平平衡.
新知讲解
例7 新学期开学,学校团委组织八年级65位新团员将教科书从仓库搬到七年级新生教室·女同学每人每次搬3包,男同学每人每次搬4包,每位同学搬了2次,共搬了450包.问:这些新团员中有多少位男同学
分析:题目告诉了我们好几个等量关系,其中有这样的等量关系:
男同学搬书包数女同学搬书包数搬书总包数.
新知讲解
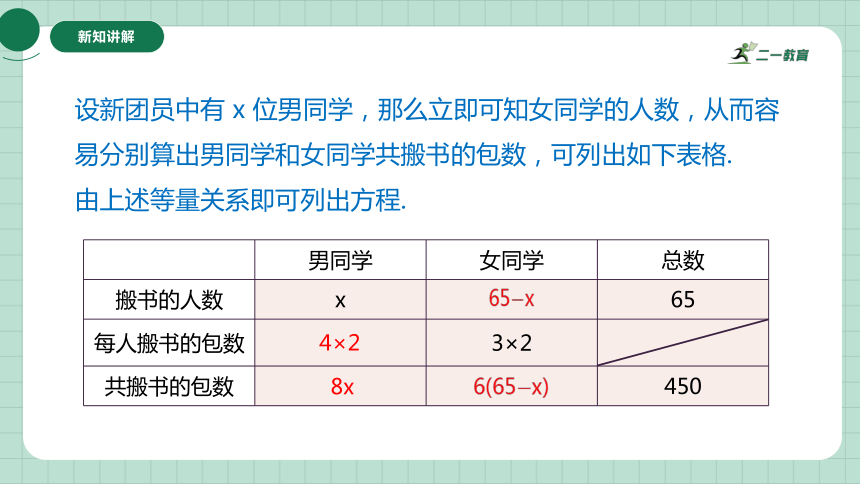
设新团员中有 x 位男同学,那么立即可知女同学的人数,从而容易分别算出男同学和女同学共搬书的包数,可列出如下表格.
由上述等量关系即可列出方程.
男同学 女同学 总数
搬书的人数 x 65
每人搬书的包数 3×2
共搬书的包数 450
4×2
8x
65x
6(65x)
新知讲解
解:设这些新团员中有 x 位男同学,根据题意,得 8x + 6(65x)= 450.
解这个方程,得
x = 30.
经检验,符合题意.
答:这些新团员中有30位男同学.
新知讲解
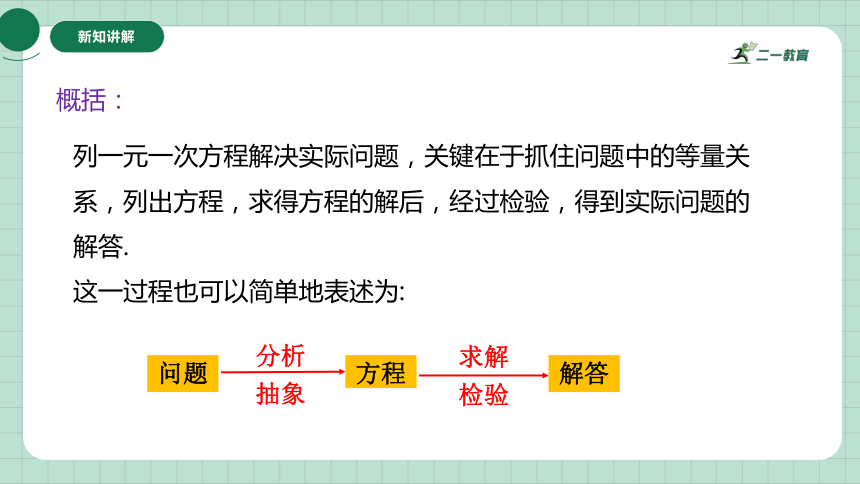
概括:
列一元一次方程解决实际问题,关键在于抓住问题中的等量关
系,列出方程,求得方程的解后,经过检验,得到实际问题的
解答.
这一过程也可以简单地表述为:
问题
方程
分析
抽象
解答
求解
检验
新知讲解
分析和抽象的过程通常包括:
(1)弄清题意和其中的数量关系,用字母表示适当的未知数(设元);
(2)找出问题中所给出的等量关系,它反映了未知量与已知量之间的关系;
(3)对这个等量关系中涉及的量,列出相关的代数式,根据等量关系,列出方程.
在设未知数和作出解答时,应注意量的单位.
新知讲解
列一元一次方程解决实际问题时需要注意以下几点:
1. 恰当地设未知数可以简化运算,且单位要统一;
2. 题中的相等关系不 一 定 只 有 一个,要根据具体情况选择;
3. 求出方程的解后要检验 .
新知讲解
试一试:
解答下面两个问题,注意比较这两个问题中的数量关系.
(1)小亮和老师一起整理了一篇教学材料,准备录入成电子稿. 按篇幅估计,老师单独录入需 4 h 完成,小亮单独录入需 6 h 完成. 小亮先录入了 1 h 后,老师开始一起录入,问:还需要多少小时完成?
分析:数量关系:小亮单独做的工作量+小亮和老师合作的工作量=总工作量,即小亮的工作效率×1+(老师的工作效率+小亮的工作效率)×x = 总工作量
设总工作量为 1 ,则老师的工作效率为 ,小亮的工作效率为 .
新知讲解
试一试:
解答下面两个问题,注意比较这两个问题中的数量关系.
(1)小亮和老师一起整理了一篇教学材料,准备录入成电子稿. 按篇幅估计,老师单独录入需 4 h 完成,小亮单独录入需 6 h 完成. 小亮先录入了 1 h 后,老师开始一起录入,问:还需要多少小时完成?
解:设还需 x 小时完成,总工作量为1,则有
×1+ ( + )x = 1,
解得 x = 2.
经检验,符合题意.
答:还需要 2 小时完成.
新知讲解
试一试:
(2)甲、乙两车分别从相距360 km的两地相向开出,已知甲车的速度为60 km/h,乙车的速度为90 km/h. 若甲车先开1 h,问:乙车开出多少小时后两车相遇?
分析:
数量关系: 甲先行驶的路程+甲、乙后行驶的路程=总路程 360 km
新知讲解
试一试:
(2)甲、乙两车分别从相距360 km的两地相向开出,已知甲车的速度为60 km/h,乙车的速度为90 km/h. 若甲车先开1 h,问:乙车开出多少小时后两车相遇?
解:设乙车开出 x 小时后两车相遇,则有
60×1+( 60+90 )x = 360,
解得 x = 2.
经检验,符合题意.
答:乙车开出 2 小时后两车相遇.
新知讲解
解一元一次方程的应用题的步骤:
审,认真审题,找数量关系
设,设未知数
列,列一元一次方程
解,解方程
检,检验答案是否符合题意
答,解答
【知识技能类作业】必做题:
课堂练习
1.某班学生分组,若每组7人,则有2人分不到组;若每组8人,则最后一组差4人.若设划分 组,则可列方程为( )
A. B.
C. D.
A
【知识技能类作业】必做题:
课堂练习
2.《九章算术》是我国古代重要的数学著作,其中记载了这样一个问题,大致意思为:现有田出租,第一年3亩1钱,第二年4亩1钱,第三年5亩1钱.三年共得100钱.问:出租的田有多少亩?设出租的田有 亩,可列方程为( )
A. B.
C. D.
B
3.小红在一家文具店买了一种大笔记本4本和一种小笔记本6本,共用了62元.已知她买的这种大笔记本的单价比这种小笔记本的单价贵3元,求该家文具店中这种大笔记本的单价.
【知识技能类作业】必做题:
课堂练习
解:设该家文具店中这种大笔记本的单价是x元,则小笔记本的单价是(x-3)元.
根据题意,得4x+6(x-3)=62,解得x=8.
经检验,符合题意.
所以该家文具店中这种大笔记本的单价是8元。
【知识技能类作业】选做题:
课堂练习
4.我国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关(里是古时距离单位).”其大意如下:“有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.”此人第三天走的路程是( )
A. 96里 B. 12里 C. 24里 D. 48里
D
5. 某校七年级(1)班学生开展分小组学习竞赛活动.原来每个小组8人,后来重新分组,每个小组6人,这样比原来增加2个小组,则七年级(1)班共有 人.
【知识技能类作业】选做题:
课堂练习
48
【综合拓展类作业】
课堂练习
6. 如图,数轴上的原点为O,A、B、C三点对应的数分别为-16、8和12,动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,同时,动点Q从点C出发,以每秒1个单位长度的速度沿数轴负方向运动.设点P的运动时间为t秒.
(1) 线段AB的长为 ,线段AC的长为 ;
(2) 当点P运动到与点A、B的距离相等的位置时,求点P对应的数;
(2) 设点P对应的数为x.由题意,得x-(-16)=
8-x,解得x=-4,即点P对应的数为-4
24
28
【综合拓展类作业】
课堂练习
(3) 当P、Q两点相遇时,求t的值;
(4) 当PO+QB=10时,直接写出t的值.
(3) 由题意,得2t+t=28,解得t=
(4) t=或t=10
课堂总结
1.列一元一次方程解决实际问题过程:
问题
方程
分析
抽象
解答
求解
检验
课堂总结
2.解一元一次方程的应用题的步骤:
审,认真审题,找数量关系
设,设未知数
列,列一元一次方程
解,解方程
检,检验答案是否符合题意
答,解答
板书设计
1.列一元一次方程解决实际问题过程:
2.解一元一次方程的应用题的步骤:
课题:5.2.2解一元一次方程(第3课时)
问题
方程
分析
抽象
解答
求解
检验
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
5.2.2解一元一次方程(第3课时)
一元一次方程
第5章
“五”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.能根据具体问题中的等量关系准确列出方程;
2.进一步体会建模思想,并能检验结果是否合理.
新知导入
48位大学生暑假到水利工地做义工,若每人每天平均挖土5 m3或运土3 m3,他们如何配合,才能使挖出的土及时运走?
若设其中x人挖土,则运土的人数为 人,根据题意,可列方程 .
(48-x)
5x=3(48-x)
新知讲解
例6 如图,天平的两个盘中分别盛有51g和45g盐,问:应从A盘中拿出多少盐放到B盘中,才能使天平平衡
分析:从 A 盘中拿出一些盐放到 B 盘中,使两盘中所盛盐的质量相等,于是有这样的等量关系:
A 盘中现有盐的质量 = B 盘中现有盐的质量.
新知讲解
设应从 A 盘中拿出 x g 盐放到 B 盘中,我们来计算两盘中现有盐的质量,可列如下表格.
A 盘 B 盘
原有盐/g 51 45
现有盐/g
51x
45x
新知讲解
解:设应从 A 盘中拿出 x g 盐放到 B 盘中,则根据题意,得
51x=45x.
解这个方程,得
x=3.
经检验,符合题意.
答:应从 A 盘中拿出 3 g 盐放到 B 盘中,才能使天平平衡.
新知讲解
例7 新学期开学,学校团委组织八年级65位新团员将教科书从仓库搬到七年级新生教室·女同学每人每次搬3包,男同学每人每次搬4包,每位同学搬了2次,共搬了450包.问:这些新团员中有多少位男同学
分析:题目告诉了我们好几个等量关系,其中有这样的等量关系:
男同学搬书包数女同学搬书包数搬书总包数.
新知讲解
设新团员中有 x 位男同学,那么立即可知女同学的人数,从而容易分别算出男同学和女同学共搬书的包数,可列出如下表格.
由上述等量关系即可列出方程.
男同学 女同学 总数
搬书的人数 x 65
每人搬书的包数 3×2
共搬书的包数 450
4×2
8x
65x
6(65x)
新知讲解
解:设这些新团员中有 x 位男同学,根据题意,得 8x + 6(65x)= 450.
解这个方程,得
x = 30.
经检验,符合题意.
答:这些新团员中有30位男同学.
新知讲解
概括:
列一元一次方程解决实际问题,关键在于抓住问题中的等量关
系,列出方程,求得方程的解后,经过检验,得到实际问题的
解答.
这一过程也可以简单地表述为:
问题
方程
分析
抽象
解答
求解
检验
新知讲解
分析和抽象的过程通常包括:
(1)弄清题意和其中的数量关系,用字母表示适当的未知数(设元);
(2)找出问题中所给出的等量关系,它反映了未知量与已知量之间的关系;
(3)对这个等量关系中涉及的量,列出相关的代数式,根据等量关系,列出方程.
在设未知数和作出解答时,应注意量的单位.
新知讲解
列一元一次方程解决实际问题时需要注意以下几点:
1. 恰当地设未知数可以简化运算,且单位要统一;
2. 题中的相等关系不 一 定 只 有 一个,要根据具体情况选择;
3. 求出方程的解后要检验 .
新知讲解
试一试:
解答下面两个问题,注意比较这两个问题中的数量关系.
(1)小亮和老师一起整理了一篇教学材料,准备录入成电子稿. 按篇幅估计,老师单独录入需 4 h 完成,小亮单独录入需 6 h 完成. 小亮先录入了 1 h 后,老师开始一起录入,问:还需要多少小时完成?
分析:数量关系:小亮单独做的工作量+小亮和老师合作的工作量=总工作量,即小亮的工作效率×1+(老师的工作效率+小亮的工作效率)×x = 总工作量
设总工作量为 1 ,则老师的工作效率为 ,小亮的工作效率为 .
新知讲解
试一试:
解答下面两个问题,注意比较这两个问题中的数量关系.
(1)小亮和老师一起整理了一篇教学材料,准备录入成电子稿. 按篇幅估计,老师单独录入需 4 h 完成,小亮单独录入需 6 h 完成. 小亮先录入了 1 h 后,老师开始一起录入,问:还需要多少小时完成?
解:设还需 x 小时完成,总工作量为1,则有
×1+ ( + )x = 1,
解得 x = 2.
经检验,符合题意.
答:还需要 2 小时完成.
新知讲解
试一试:
(2)甲、乙两车分别从相距360 km的两地相向开出,已知甲车的速度为60 km/h,乙车的速度为90 km/h. 若甲车先开1 h,问:乙车开出多少小时后两车相遇?
分析:
数量关系: 甲先行驶的路程+甲、乙后行驶的路程=总路程 360 km
新知讲解
试一试:
(2)甲、乙两车分别从相距360 km的两地相向开出,已知甲车的速度为60 km/h,乙车的速度为90 km/h. 若甲车先开1 h,问:乙车开出多少小时后两车相遇?
解:设乙车开出 x 小时后两车相遇,则有
60×1+( 60+90 )x = 360,
解得 x = 2.
经检验,符合题意.
答:乙车开出 2 小时后两车相遇.
新知讲解
解一元一次方程的应用题的步骤:
审,认真审题,找数量关系
设,设未知数
列,列一元一次方程
解,解方程
检,检验答案是否符合题意
答,解答
【知识技能类作业】必做题:
课堂练习
1.某班学生分组,若每组7人,则有2人分不到组;若每组8人,则最后一组差4人.若设划分 组,则可列方程为( )
A. B.
C. D.
A
【知识技能类作业】必做题:
课堂练习
2.《九章算术》是我国古代重要的数学著作,其中记载了这样一个问题,大致意思为:现有田出租,第一年3亩1钱,第二年4亩1钱,第三年5亩1钱.三年共得100钱.问:出租的田有多少亩?设出租的田有 亩,可列方程为( )
A. B.
C. D.
B
3.小红在一家文具店买了一种大笔记本4本和一种小笔记本6本,共用了62元.已知她买的这种大笔记本的单价比这种小笔记本的单价贵3元,求该家文具店中这种大笔记本的单价.
【知识技能类作业】必做题:
课堂练习
解:设该家文具店中这种大笔记本的单价是x元,则小笔记本的单价是(x-3)元.
根据题意,得4x+6(x-3)=62,解得x=8.
经检验,符合题意.
所以该家文具店中这种大笔记本的单价是8元。
【知识技能类作业】选做题:
课堂练习
4.我国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关(里是古时距离单位).”其大意如下:“有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地.”此人第三天走的路程是( )
A. 96里 B. 12里 C. 24里 D. 48里
D
5. 某校七年级(1)班学生开展分小组学习竞赛活动.原来每个小组8人,后来重新分组,每个小组6人,这样比原来增加2个小组,则七年级(1)班共有 人.
【知识技能类作业】选做题:
课堂练习
48
【综合拓展类作业】
课堂练习
6. 如图,数轴上的原点为O,A、B、C三点对应的数分别为-16、8和12,动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,同时,动点Q从点C出发,以每秒1个单位长度的速度沿数轴负方向运动.设点P的运动时间为t秒.
(1) 线段AB的长为 ,线段AC的长为 ;
(2) 当点P运动到与点A、B的距离相等的位置时,求点P对应的数;
(2) 设点P对应的数为x.由题意,得x-(-16)=
8-x,解得x=-4,即点P对应的数为-4
24
28
【综合拓展类作业】
课堂练习
(3) 当P、Q两点相遇时,求t的值;
(4) 当PO+QB=10时,直接写出t的值.
(3) 由题意,得2t+t=28,解得t=
(4) t=或t=10
课堂总结
1.列一元一次方程解决实际问题过程:
问题
方程
分析
抽象
解答
求解
检验
课堂总结
2.解一元一次方程的应用题的步骤:
审,认真审题,找数量关系
设,设未知数
列,列一元一次方程
解,解方程
检,检验答案是否符合题意
答,解答
板书设计
1.列一元一次方程解决实际问题过程:
2.解一元一次方程的应用题的步骤:
课题:5.2.2解一元一次方程(第3课时)
问题
方程
分析
抽象
解答
求解
检验
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
