新疆奎屯市第八中学人教版八年级数学下册:18.2.1矩形的性质 课件(共14张PPT)
文档属性
| 名称 | 新疆奎屯市第八中学人教版八年级数学下册:18.2.1矩形的性质 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 175.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-28 07:36:34 | ||
图片预览




文档简介
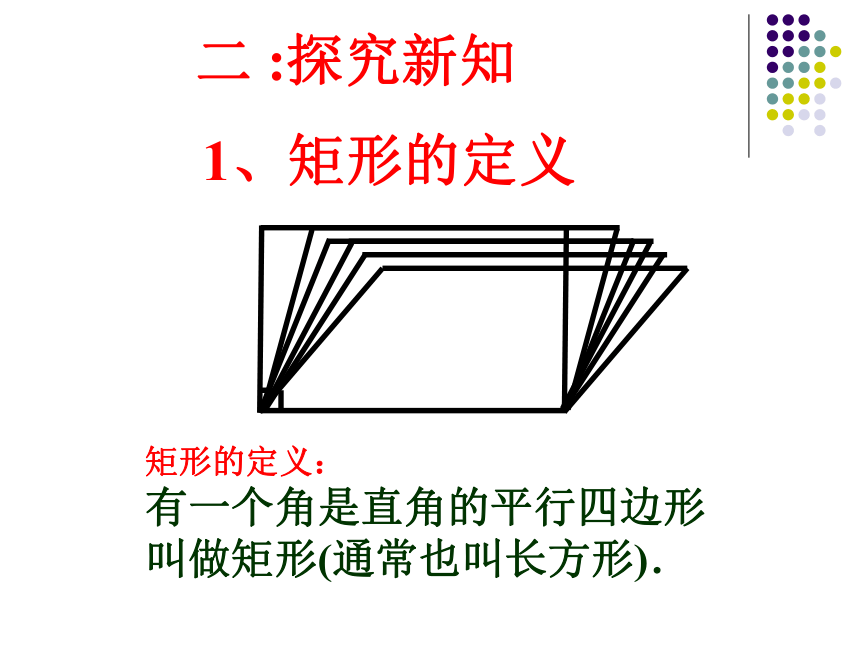
课件14张PPT。边:对边平行且相等.
角:对角相等邻角互补.对角线:对角线互相平分.平行四边形的性质ABCD一、知识回顾:O对称性:中心对称图形.生
活
中
的
矩
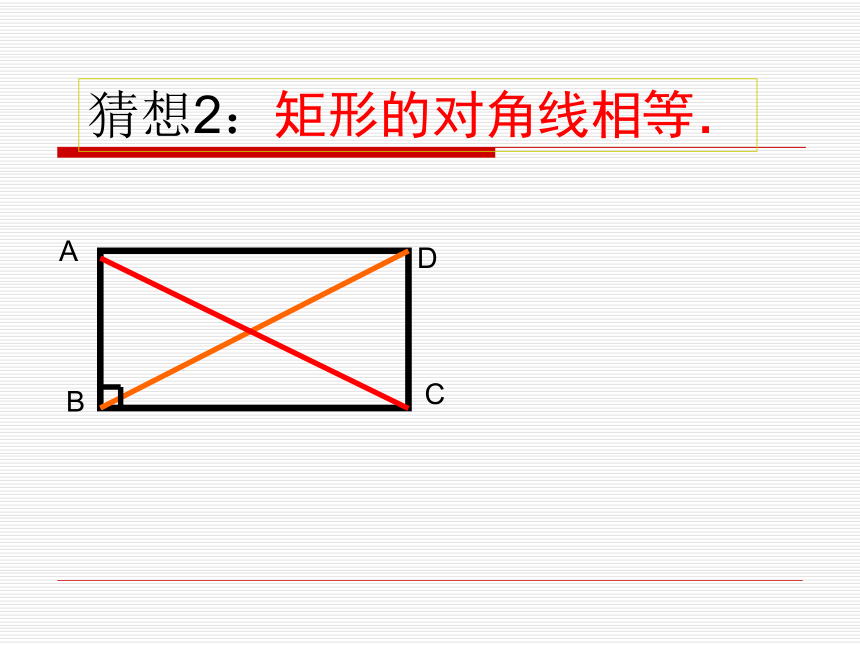
形1、矩形的定义矩形的定义:
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).二 :探究新知 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,猜想还有哪些特殊性质呢?猜想1:ABCD2、矩形的性质矩形的四个角都是直角. 1:矩形的四个角都是直角已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°DCBA证明:
∵矩形ABCD是平行四边形(已知)
∴ ∠B+∠C=180 °(平行四边形邻角互补)
又 ∵ ∠B=90° (已知)
∴ ∠C=90 °(等式的性质)
同理:∠D=90° ,∠A=90°
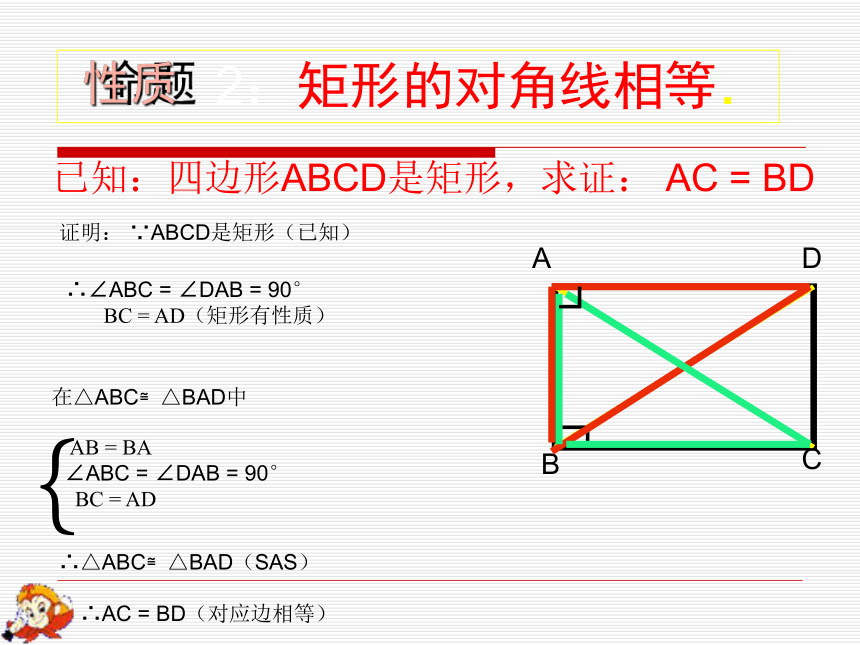
∴∠A=∠B=∠C=∠D=90°命题性质猜想2:矩形的对角线相等.ABCD已知:四边形ABCD是矩形,求证: AC = BD 证明: ∵ABCD是矩形(已知)∴∠ABC = ∠DAB = 90°
BC = AD(矩形有性质)∴△ABC≌△BAD(SAS)∴AC = BD(对应边相等) 2:矩形的对角线相等.命题性质在△ABC≌△BAD中 AB = BA
∠ABC = ∠DAB = 90°
BC = AD{矩形的对称性:O中心对称图形轴对称图形比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形ODCBA┛ 问题:提问:⑴如图,通过以上对矩形性质的探究,你能进一步发现图中有多少个直角三角形吗?有多少个等腰三角形吗?你能发现线段AO、CO、BO、DO之间的大小关系吗?这四条线段与AC、BD又是什么关系呢?如果只看直角三角形ABC, AO是BD边上的什么线?你能说说这个结论吗? ODCBA┛在Rt△ABD中,AO是斜边BD的中线直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。则有:AO= BD 试试:用文字叙述
直角三角形斜边上中线的性质 在矩形ABCD中
AO=CO=BO=DO= AC= BD
1、矩形具有而平行四边行不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等
2、矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
(A)20° (B)40° (C)60° (D)80°
3、两条直角边的长分别为12和5,则斜边上的中线( )(A)26 (B)13 (C)8。5 (D)6。5
4、已知:如图,矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,则矩形对角线的长为 cmBDD85、如果矩形的一条对角线的长为8 cm,两条对角线的一个交角为120°,求矩形的边长 6、如图:矩形ABCD的两条对角线
相交于点O,CE‖OB交AB的延长线
于点E,试证明AC与CE的大小关系。
B我的收获从一般到特殊边角对角线矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;
直角三角形斜边上的中线等于斜边的一半. 直角三角形斜边上的中线性质 矩形的定义:
有一个角是直角的平行四边形叫做矩形
角:对角相等邻角互补.对角线:对角线互相平分.平行四边形的性质ABCD一、知识回顾:O对称性:中心对称图形.生
活
中
的
矩
形1、矩形的定义矩形的定义:
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).二 :探究新知 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,猜想还有哪些特殊性质呢?猜想1:ABCD2、矩形的性质矩形的四个角都是直角. 1:矩形的四个角都是直角已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°DCBA证明:
∵矩形ABCD是平行四边形(已知)
∴ ∠B+∠C=180 °(平行四边形邻角互补)
又 ∵ ∠B=90° (已知)
∴ ∠C=90 °(等式的性质)
同理:∠D=90° ,∠A=90°
∴∠A=∠B=∠C=∠D=90°命题性质猜想2:矩形的对角线相等.ABCD已知:四边形ABCD是矩形,求证: AC = BD 证明: ∵ABCD是矩形(已知)∴∠ABC = ∠DAB = 90°
BC = AD(矩形有性质)∴△ABC≌△BAD(SAS)∴AC = BD(对应边相等) 2:矩形的对角线相等.命题性质在△ABC≌△BAD中 AB = BA
∠ABC = ∠DAB = 90°
BC = AD{矩形的对称性:O中心对称图形轴对称图形比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形ODCBA┛ 问题:提问:⑴如图,通过以上对矩形性质的探究,你能进一步发现图中有多少个直角三角形吗?有多少个等腰三角形吗?你能发现线段AO、CO、BO、DO之间的大小关系吗?这四条线段与AC、BD又是什么关系呢?如果只看直角三角形ABC, AO是BD边上的什么线?你能说说这个结论吗? ODCBA┛在Rt△ABD中,AO是斜边BD的中线直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。则有:AO= BD 试试:用文字叙述
直角三角形斜边上中线的性质 在矩形ABCD中
AO=CO=BO=DO= AC= BD
1、矩形具有而平行四边行不具有的的性质是( )
(A)对角相等 (B)对角线相等
(C)对角线互相平分 (D)对边平行且相等
2、矩形的一条对角线与一边的夹角为40°,则两条对角线相交所成的锐角是( )
(A)20° (B)40° (C)60° (D)80°
3、两条直角边的长分别为12和5,则斜边上的中线( )(A)26 (B)13 (C)8。5 (D)6。5
4、已知:如图,矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,则矩形对角线的长为 cmBDD85、如果矩形的一条对角线的长为8 cm,两条对角线的一个交角为120°,求矩形的边长 6、如图:矩形ABCD的两条对角线
相交于点O,CE‖OB交AB的延长线
于点E,试证明AC与CE的大小关系。
B我的收获从一般到特殊边角对角线矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;
直角三角形斜边上的中线等于斜边的一半. 直角三角形斜边上的中线性质 矩形的定义:
有一个角是直角的平行四边形叫做矩形
