2025年山东省济宁市中考数学模拟试题(含详解)
文档属性
| 名称 | 2025年山东省济宁市中考数学模拟试题(含详解) |  | |
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 23:05:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年山东省济宁市中考数学模拟试题
考试时间:120分钟;总分:100分
学校:___________姓名:___________班级:___________考号:___________
1. 选择题(共10小题,满分30分,每小题3分)
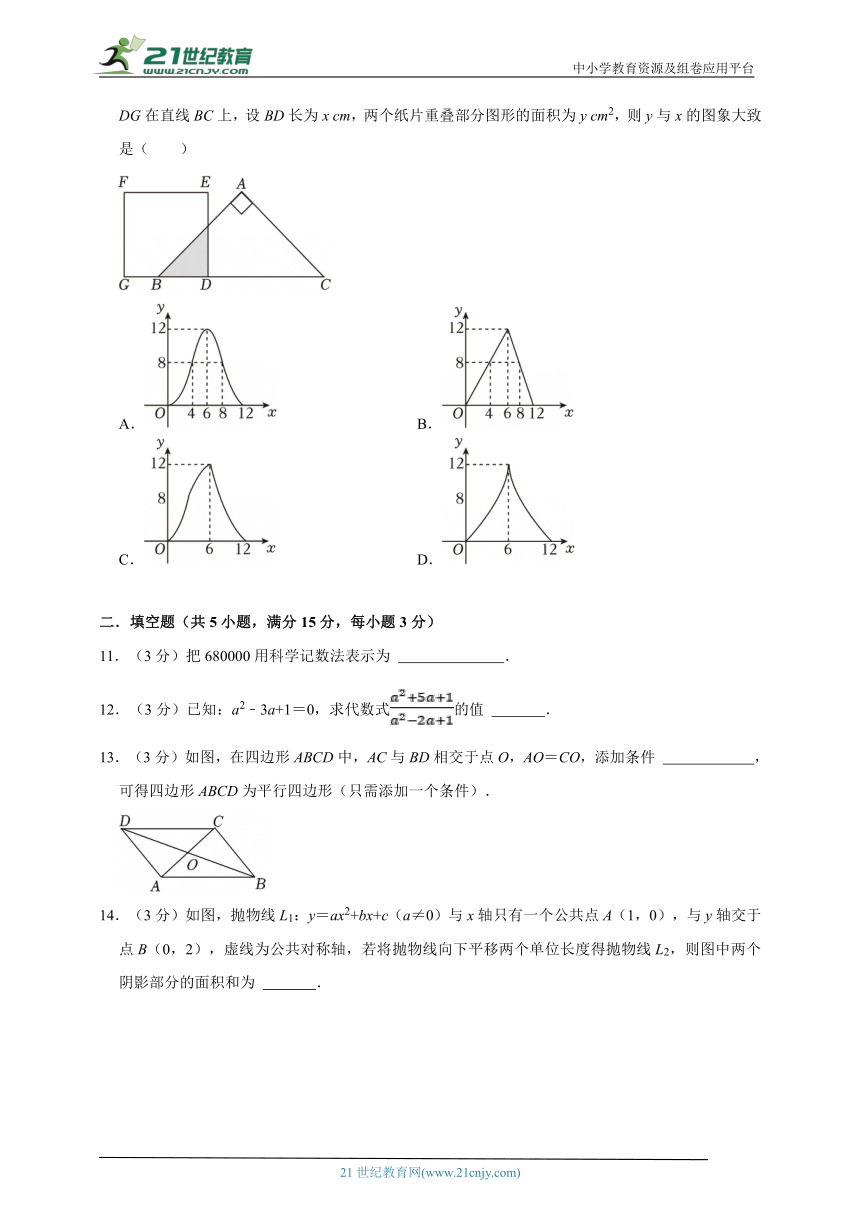
1.(3分)自然数2的相反数是( )
A.1 B.﹣1 C.﹣2 D.2
2.(3分)一个几何体如图1放置,如图2可能是它的( )
A.主视图 B.左视图 C.俯视图 D.不能确定
3.(3分)“一方有难,八方支援”,各省市都斥资到抗疫前线,据有关部门初步统计,国家已经投入资金1390亿元用于抗疫防控.将139000000000用科学记数法表示为( )
A.1.39×108 B.1.39×109 C.1.39×1010 D.1.39×1011
4.(3分)如图,点A是半径为5的⊙O上任意一点,以点A为圆心,OA为半径画弧,交⊙O于点B,以点B为圆心,OA为半径画弧交⊙O于点C,同上述作图方法逆时针作出点D,E,F,依次连接A→B→C→D→E→F→A,则这个多边形的内角和度数为( )
A.720° B.540° C.120° D.60°
5.(3分)如图,△ABC≌△A′B′C′,则∠B的度数为( )
A.30° B.50° C.90° D.100°
6.(3分)下列计算正确的是( )
A.2a+3a2=5a2 B.(﹣3a)2=6a2
C.2(a﹣b)=2a﹣b D.a2 a5=a7
7.(3分)一元二次方程﹣x2+2022x+2035=0的根的情况是( )
A.没有实数根
B.有两个相等的实数根
C.只有一个实数根
D.有两个不相等的实数根
8.(3分)如图,电路图有4只未闭合的开关,一个电源和一个小灯泡,已知电路图上的每个部分都能正常工作,任意闭合其中两只开关,使得小灯泡发光的概率为( )
A. B. C. D.
9.(3分)已知在正方形ABCD中,AB长为6,分别以A,B为圆心,以大于AB长度的一半为半径作弧,两弧交于M、N两点,作直线MN,交CD于点E,再分别以A,E为圆心,以大于AE长的一半为半径作弧,两弧交于P、Q两点,作直线PQ,分别与AD,BC交于点F、G,那么四边形AFGB的面积为( )
A.18 B. C. D.
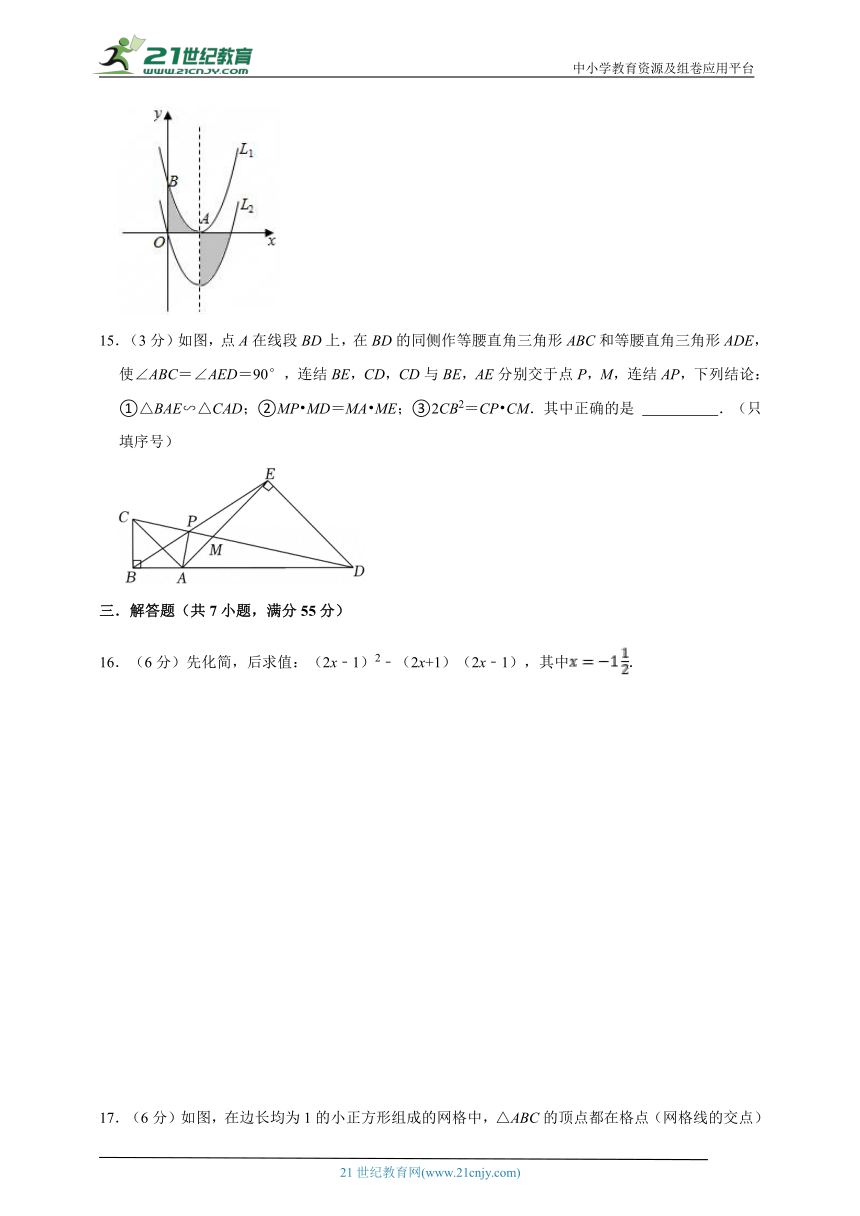
10.(3分)如图,等腰直角三角形纸片ABC,底边BC长为8cm,边长为4cm的正方形纸片的边DG在直线BC上,设BD长为x cm,两个纸片重叠部分图形的面积为y cm2,则y与x的图象大致是( )
A. B.
C. D.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)把680000用科学记数法表示为 .
12.(3分)已知:a2﹣3a+1=0,求代数式的值 .
13.(3分)如图,在四边形ABCD中,AC与BD相交于点O,AO=CO,添加条件 ,可得四边形ABCD为平行四边形(只需添加一个条件).
14.(3分)如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为公共对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为 .
15.(3分)如图,点A在线段BD上,在BD的同侧作等腰直角三角形ABC和等腰直角三角形ADE,使∠ABC=∠AED=90°,连结BE,CD,CD与BE,AE分别交于点P,M,连结AP,下列结论:①△BAE∽△CAD;②MP MD=MA ME;③2CB2=CP CM.其中正确的是 .(只填序号)
三.解答题(共7小题,满分55分)
16.(6分)先化简,后求值:(2x﹣1)2﹣(2x+1)(2x﹣1),其中.
17.(6分)如图,在边长均为1的小正方形组成的网格中,△ABC的顶点都在格点(网格线的交点)上.
(1)将△ABC向右平移4个单位长度,再向下平移3个单位长度,得到△A1B1C1,画出△A1B1C1.
(2)将△ABC绕点C顺时针旋转90°,得到△A2B2C,画出△A2B2C.
(3)在(2)的旋转过程中,点A经过的路径长是 .
18.(8分)某学校射击队计划从甲、乙两名运动员中选取一名队员代表该校参加比赛,在选拔过程中,每名选手射击10次,根据甲、乙队员成绩绘制了如图1、图2所示的统计图;并求得了乙队员10次射击成绩的平均数和方差:7环,s乙2[3×(6﹣7)2+(5﹣7)2+(4﹣7)2+(7﹣7)2+2×(9﹣7)2+(10﹣7)2+(8﹣7)2]=3.4.
(1)甲队员选拔赛成绩的众数是 环,乙队员选拔赛成绩的中位数是 环;
(2)求甲队员10次射击成绩的平均数和方差,根据甲、乙两名队员的选拔赛成绩,你推荐谁代表学校参加比赛,并说明理由;
(3)为提升射击队技战术水平,学校决定除甲、乙外,再从射击队其他4名队员(三名男生,一名女生)中随机选出两名队员一同前往观看比赛,用列表或画树形图的方法求出恰好选出一名男生利一名女生的概率.
19.(8分)小邕做数学题时遇到了如下问题:如图1,△ABD是⊙O的内接三角形,直线l经过点A,点E是直线l上的一点且∠ABD=∠DAE.求证:直线l是⊙O的切线.小邕添加了适当的辅助线后,得到了图2的图形,并利用它解决了问题.
(1)请你根据小邕的思考,写出解决这一问题的过程;
(2)在图3中,作直径BC,连接CD,得到图3.若∠DAE=30°,AD=2,AB=8,求CD的长.
20.(8分)某商家销售一种糕点,每盒进价为40元.在销售过程中发现,周销量y(盒)与销售单价x(元)之间满足一次函数关系,其部分对应数据如表所示:
销售单价x(元) … 60 65 70 …
周销量y(盒) … 240 210 180 …
(1)求y关于x的函数表达式.
(2)当销售单价定为多少元时,每周出售这种糕点所获利润最大?最大利润为多少元?
(3)若规定销售单价需满足50≤x≤80,则每周至少可获得多少利润?
21.(9分)在矩形ABCD中,AB=4,BC=2,动点P从A出发,以1个单位每秒速度,沿射线AB方向运动,同时,动点Q从点C出发,以2个单位每秒速度,沿射线BC方向运动,设运动时间为t秒,连结DP,DQ.
(1)如图1.证明:DP⊥DQ.
(2)作∠PDQ平分线交直线BC于点E;
①图2,当点E与点B重合时,求t的值.
②连结PE,PQ,当△PBE与△PDQ相似时,求t的值.
22.(10分)如图,抛物线y=ax2+bx﹣6与x轴交于点A(﹣6,0)和点B(2,0).与y轴交于点C,连接AC,BC.
(1)求该抛物线的函数解析式.
(2)点P是直线AC下方抛物线上的一个动点,过点P作BC的平行线l,交线段AC于D.
①试探究:在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,求出点E的坐标;若不存在,请说明理由;
②设抛物线的对称轴与直线l交于点M,与直线AC交于点N.当S△DMN=S△AOC时,请直接写出DM的长.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:2的相反数是﹣2.
选:C.
2.解:从图1的左面看到的图形与图2相同,因此图2可能是它的左视图,B正确.
选:B.
3.解:139000000000=1.39×1011.
选:D.
4.解:由题意可得六边形ABCDEF是⊙O的内接正六边形,
所以六边形的内角和为(6﹣2)×180°=720°,
选:A.
5.解:∵△ABC≌△A′B′C′,∠C'=30°,
∴∠C=∠C′=30°,
在△ABC中,∠A=50°,∠C=30°,
∴∠B=180°﹣(∠A+∠C)=180°﹣(50°+30°)=100°;
选:D.
6.解:A、2a与3a2不是同类项,不能合并,此选项不符合题意;
B、(﹣3a)2=9a2,此选项不符合题意;
C、2(a﹣b)=2a﹣2b,此选项不符合题意;
D、a2 a5=a7,此选项符合题意;
选:D.
7.解:∵Δ=b2﹣4ac=20222﹣4×(﹣1)×2035>0,
∴一元二次方程﹣x2+2022x+2035=0有两个不相等的实数根,
选:D.
8.解:将4只未闭合的开关从上到下分别记为A,B,C,D,
则闭合开关A和D或闭合开关B和D时,小灯泡发光.
列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
共有12种等可能的结果,其中使得小灯泡发光的结果有:(A,D),(B,D),(D,A),(D,B),共4种,
∴使得小灯泡发光的概率为.
选:B.
9.解:如图,过点F作FH⊥BC于点H.则四边形CDFH是矩形,设AE交BF于点J.
∵四边形ABCD是正方形,
∴AB=AD=CD=BC=6,∠ADE=90°,
由作图可知MN垂直平分AB,FG垂直平分线段AE,
∴MN是正方形ABCD的对称轴,
∴DE=EC=3,
在Rt△ADE中,AE3,
∴AJ=JE,
∵cos∠DAE,
∴,
∴AF,
∵∠DAE+∠AFJ=90°,∠HFG+∠AFJ=90°,
∴∠DAE=∠HFG,
∵∠ADE=∠FHG=90°,FH=CD=AD,
∴△ADE≌△FHG(ASA),
∴DE=GH=3,
∵AF=BH,
∴BG=BH=GH3,
∴四边形AFGB的面积()×6.
选:B.
10.解:∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∵四边形CDEF是边长为4的正方形,且边DG在直线BC上,
∴∠CDE=∠DCF=90°,DG=4cm,
当0≤x≤4时,如图,DE交AB于点H,
则△BDH为等腰直角三角形,
∴BD=DH=x cm,
∴y=S△BDH( cm2);
当4<x≤8时,如图,过A作AO⊥BC于点O,CF交AB于点M,DE交AC于点N,
则△BMG和△CDN为等腰三角形,AOBC=4cm,
∴GM=BG=BD﹣DG=(x﹣4)cm,DN=CD=BC﹣BD=(8﹣x)cm,
∴y=S△ABC﹣S△BCM﹣S△CDN(x﹣6)2+12;
当8<x≤12时,如图,CF交AC于点P,
则△CGP为等腰直角三角形,
∵CD=BD﹣BC=(x﹣8)cm,
∴PG=CG=DG﹣CD=(12﹣x)cm,
∴y=S△CGP.
综上,.
选:A.
二.填空题(共5小题,满分15分,每小题3分)
11.解:680000=6.8×105.
答案为:6.8×105.
12.解:∵a2﹣3a+1=0,
∴a2=3a﹣1,
∴
=8,
答案为:8.
13.解:添加条件DO=BO,
证明:∵AO=CO,DO=BO,
∴四边形ABCD为平行四边形,
答案为:DO=BO.
14.解:过抛物线L2的顶点D作CD∥x轴,与y轴交于点C,如图所示:
则四边形OCDA是矩形,
∵抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),
∴OB=2,OA=1,
将抛物线L1向下平移两个单位长度得抛物线L2,则AD=OC=2,
由图可知,阴影部分的面积等于矩形OCDA的面积,
∴S阴影部分=S矩形OCDA=OA AD=1×2=2.
答案为:2.
15.解:∵△ABC和△ADE是等腰直角三角形,
∴ACABCB,ADAE,
∴.
∵∠BAC=∠EAD=45°,
∴∠BAE=∠CAD,
∴△BAE∽△CAD,①正确.
∵△BAE∽△CAD,
∴∠BEA=∠CDA.
∵∠PME=∠AMD,
∴△PME∽△AMD,
∴,
∴MP MD=MA ME,②正确.
由②得MP MD=MA ME,
∴.
∵∠PMA=∠EMD,
∴△PMA∽△EMD,
∴∠APD=∠AED=90°.
∵∠CAE=180°﹣∠BAC﹣∠EAD=90°,
∴∠APD=∠CAE.
∵∠APD=∠CAE,∠C是公共角,
∴△CAP∽△CMA,
∴,
∴AC2=CP CM.
∵ACCB,
∴2CB2=CP CM,③正确.
答案为:①②③.
三.解答题(共7小题,满分55分)
16.解:原式=4x2﹣4x+1﹣[(2x)2﹣1]
=4x2﹣4x+1﹣4x2+1
=2﹣4x,
当时,原式.
17.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C即为所求.
(3)由勾股定理得,AC,
∴点A经过的路径长是.
答案为:.
18.解:(1)甲的成绩中,7环与8环都出现了3次,次数最多,众数为7环与8环;
把乙队员选拔赛成绩按从小到大的顺序排列,中位数是第5、第6个数的平均数,
则乙队员选拔赛成绩的中位数是6.5(环);
答案为:7与8,6.5;
(2)推荐甲队代表学校参加比赛.理由如下:
甲队的平均数是(环),
甲队的方差是:;
∵8>7,1.6<3.4,
∴甲以代表学校参加比赛;
(3)列表如下:
男1 男2 男3 女
男1 (男1,男2) (男1,男3) (男1,女)
男2 (男2,男1) (男2,男3) (男2,女)
男3 (男3,男1) (男3,男2) (男3,女)
女 (女,男1) (女,男2) (女,男3)
共有12种等可能的情况数,其中恰好选出一名男生和一名女生的有6种,
则恰好选出一名男生和一名女生的概率是.
19.(1)证明:如图2,作直径AF,连接DF,
则∠ADF=90°,
∴∠DAF+∠AFD=90°,
由圆周角定理得:∠ABD=∠AFD,
∵∠ABD=∠DAE,
∴∠DAE=∠AFD,
∴∠DAF+∠DAE=90°,
∴∠FAE=90°,
∵AF是⊙O的直径,
∴直线l是⊙O的切线;
(2)解:如图3,过点A作AH⊥BD于H,
∵∠DAE=30°,∠ABD=∠DAE,
∴∠ABD=∠DAE=30°,AF=2AD=4,
∴AHAB=4,BHAB=4,
由勾股定理得:DH2,
∴BD=BH+DH=6,
∴CD2.
20.解:(1)由题意,设y关于x的函数表达式为y=kx+b,
∴.
∴.
∴y关于x的函数表达式为y=﹣6x+600.
(2)由题意,可得每周出售这种糕点所获利润=(x﹣40)(﹣6x+600)
=﹣6x2+840x﹣24000
=﹣6(x﹣70)2+5400.
∵﹣6<0,
∴当x=70时,每周出售这种糕点所获利润最大,最大利润为5400元.
(3)由(2)每周出售这种糕点所获利润=﹣6(x﹣70)2+5400.
又∵50≤x≤80,
∴当x=50时,所获利润最小为3000元;当x=70时,所获利润最大为5400元.
∴销售单价需满足50≤x≤80,则每周至少可获得3000元的利润.
21.(1)证明:∵四边形ABCD是矩形,AB=4,BC=2,
∴∠A=∠DCQ=∠ADC=90°,
∴∠ADP+∠CDP=90°,
∵AB=CD=4,BC=AD=2,
∵AP=t,CQ=2t,
∴,
∴△ADP∽△CDQ,
∴∠ADP=∠CDQ,
∴∠CDQ+∠CDP=90°,即∠PDQ=90°,
∴DP⊥DQ;
(2)①解:∵DB平分∠PDQ,
∴∠PDB=∠BDQ=45°,
过点P作PF⊥BD交于点F,
∴PF=DF,
∵AP=t,AD=2,
∴DP,
∴PF,
∵sin∠ABD,
解得t或t=﹣6(舍);
②解:当P与A点重合时,△PBE≌△QDP,t=0;
以B为坐标原点,BC所在的直线为x轴,AB所在的直线为y轴,建立了直角坐标系,
∵AB=6,BC=2,
∴A(0,6),B(2,0),
∴D(2,6),
∵AP=t,CQ=2t,
∴P(0,4﹣t),Q(2+2t,0),
取DQ的中点M,连接EM,
∴M(2+t,2),
∵DE平分∠PDQ,
∴∠PDE=∠QDE,
∵CD=2AD,CQ=2AP,∠PDQ=90°,
∴△ADP∽△CDQ,
∴DQ=2AP,
∴DM=PD,
∴△PDE≌△MDE(SAS),
∴EP=EM,
当E点在C点左侧时,如图3﹣1﹣1,此时△PBE∽△QDP,
∴PB=BE,
∵PB=4﹣t,
∴BE=2t,
∴E(2t,0),
∴(4﹣t)2+(2t)2=(2t﹣2﹣t)2+4,
解得t=﹣5或t=﹣5(舍);
当E点在C点右侧,P点在BC上方时,如图3﹣2,△PBE∽△PDQ,
此时E(8﹣2t,0),
∴(6﹣3t)2+4=(4﹣t)2+(8﹣2t)2,
解得t或t(舍);
当E点在C点右侧,P点在BC下方时,如图3﹣3,△PBE∽△PDQ,
此时E(2t﹣8,0),P(4﹣t,0),
∴(4﹣t)2+(8﹣2t)2=(t﹣10)2+4,
解得t=1(舍)或t=6;
当E点在C点右侧,P点在BC下方时,如图3﹣4,△PBE∽△QDP,
此时E(t﹣2,0),P(4﹣t,0),
∴(4﹣t)2+(t﹣2)2=(t+4)2+4,
解得t=0(舍)或t=14;
综上所述:t的值为0或6或14或或﹣5.
22.解:(1)把点A(﹣6,0)和点B(2,0)代入抛物线y=ax2+bx﹣6得,
解得,
∴抛物线的函数解析式yx2+2x﹣6;
(2)①存在:
∵抛物线的函数解析式yx2+2x﹣6交y轴于C,
∴C(0,﹣6),
∵A(﹣6,0),
∴直线AC的解析式为y=﹣x﹣6,
设点D的坐标为(m,﹣m﹣6),其中﹣6<m<0,
∵B(2,0),C(0,﹣6),
∴BD2=(m﹣2)2+(m+6)2,BC2=22+62=40,DC2=m2+(﹣m﹣6+6)2=2m2,
∵DE∥BC,
∴当DE=BC时,以点D,C,B,E为顶点的四边形为平行四边形,
分两种情况:
如图,当BD=BC时,四边形BDEC为菱形,
∴BD2=BC2,
∴(m﹣2)2+(m+6)2=40,
解得:m1=﹣4,m2=0(舍去),
∴点D的坐标为(﹣4,﹣2),
∵点D向左移动2各单位长度,向下移动6个单位长度得到点E,
∴点E的坐标为(﹣6,﹣8);
如图,当CD=CB时,四边形CBED为菱形,
∴CD2=CB2,
∴2m2=40,
解得:m1=﹣2,m2=2(舍去),
∴点D的坐标为(﹣2,26),
∵点D向右移动2个单位长度,向上移动6个单位长度得到点E,
∴点E的坐标为(2﹣2,2);
综上,存在点E,使得以点D,C,B,E为顶点的四边形为菱形,点E的坐标为(﹣6,﹣8)或(2﹣2,2);
②设点D的坐标为(m,﹣m﹣6),其中﹣6<m<0,
∵A(﹣6,0),B(2,0),
∴抛物线的对称轴为直线x=﹣2,
∵直线BC的函数表达式为y=3x﹣6,直线l∥BC,
∴设直线l的解析式为y=3x+b,
∵点D的坐标(m,﹣m﹣6),
∴b=﹣4m﹣6,
∴M(﹣2,﹣4m﹣12),
∵抛物线的对称轴与直线AC交于点N,
∴N(﹣2,﹣4),
∴MN=﹣4m﹣12+4=﹣4m﹣8,
∵S△DMN=S△AOC,
∴(﹣4m﹣8)(﹣2﹣m)6×6,
整理得:m2+4m﹣5=0,
解得:m1=﹣5,m2=1(舍去),
∴点D的坐标为(﹣5,﹣1),
∴点M的坐标为(﹣2,8),
∴DM3,
答:DM的长为3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025年山东省济宁市中考数学模拟试题
考试时间:120分钟;总分:100分
学校:___________姓名:___________班级:___________考号:___________
1. 选择题(共10小题,满分30分,每小题3分)
1.(3分)自然数2的相反数是( )
A.1 B.﹣1 C.﹣2 D.2
2.(3分)一个几何体如图1放置,如图2可能是它的( )
A.主视图 B.左视图 C.俯视图 D.不能确定
3.(3分)“一方有难,八方支援”,各省市都斥资到抗疫前线,据有关部门初步统计,国家已经投入资金1390亿元用于抗疫防控.将139000000000用科学记数法表示为( )
A.1.39×108 B.1.39×109 C.1.39×1010 D.1.39×1011
4.(3分)如图,点A是半径为5的⊙O上任意一点,以点A为圆心,OA为半径画弧,交⊙O于点B,以点B为圆心,OA为半径画弧交⊙O于点C,同上述作图方法逆时针作出点D,E,F,依次连接A→B→C→D→E→F→A,则这个多边形的内角和度数为( )
A.720° B.540° C.120° D.60°
5.(3分)如图,△ABC≌△A′B′C′,则∠B的度数为( )
A.30° B.50° C.90° D.100°
6.(3分)下列计算正确的是( )
A.2a+3a2=5a2 B.(﹣3a)2=6a2
C.2(a﹣b)=2a﹣b D.a2 a5=a7
7.(3分)一元二次方程﹣x2+2022x+2035=0的根的情况是( )
A.没有实数根
B.有两个相等的实数根
C.只有一个实数根
D.有两个不相等的实数根
8.(3分)如图,电路图有4只未闭合的开关,一个电源和一个小灯泡,已知电路图上的每个部分都能正常工作,任意闭合其中两只开关,使得小灯泡发光的概率为( )
A. B. C. D.
9.(3分)已知在正方形ABCD中,AB长为6,分别以A,B为圆心,以大于AB长度的一半为半径作弧,两弧交于M、N两点,作直线MN,交CD于点E,再分别以A,E为圆心,以大于AE长的一半为半径作弧,两弧交于P、Q两点,作直线PQ,分别与AD,BC交于点F、G,那么四边形AFGB的面积为( )
A.18 B. C. D.
10.(3分)如图,等腰直角三角形纸片ABC,底边BC长为8cm,边长为4cm的正方形纸片的边DG在直线BC上,设BD长为x cm,两个纸片重叠部分图形的面积为y cm2,则y与x的图象大致是( )
A. B.
C. D.
二.填空题(共5小题,满分15分,每小题3分)
11.(3分)把680000用科学记数法表示为 .
12.(3分)已知:a2﹣3a+1=0,求代数式的值 .
13.(3分)如图,在四边形ABCD中,AC与BD相交于点O,AO=CO,添加条件 ,可得四边形ABCD为平行四边形(只需添加一个条件).
14.(3分)如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),虚线为公共对称轴,若将抛物线向下平移两个单位长度得抛物线L2,则图中两个阴影部分的面积和为 .
15.(3分)如图,点A在线段BD上,在BD的同侧作等腰直角三角形ABC和等腰直角三角形ADE,使∠ABC=∠AED=90°,连结BE,CD,CD与BE,AE分别交于点P,M,连结AP,下列结论:①△BAE∽△CAD;②MP MD=MA ME;③2CB2=CP CM.其中正确的是 .(只填序号)
三.解答题(共7小题,满分55分)
16.(6分)先化简,后求值:(2x﹣1)2﹣(2x+1)(2x﹣1),其中.
17.(6分)如图,在边长均为1的小正方形组成的网格中,△ABC的顶点都在格点(网格线的交点)上.
(1)将△ABC向右平移4个单位长度,再向下平移3个单位长度,得到△A1B1C1,画出△A1B1C1.
(2)将△ABC绕点C顺时针旋转90°,得到△A2B2C,画出△A2B2C.
(3)在(2)的旋转过程中,点A经过的路径长是 .
18.(8分)某学校射击队计划从甲、乙两名运动员中选取一名队员代表该校参加比赛,在选拔过程中,每名选手射击10次,根据甲、乙队员成绩绘制了如图1、图2所示的统计图;并求得了乙队员10次射击成绩的平均数和方差:7环,s乙2[3×(6﹣7)2+(5﹣7)2+(4﹣7)2+(7﹣7)2+2×(9﹣7)2+(10﹣7)2+(8﹣7)2]=3.4.
(1)甲队员选拔赛成绩的众数是 环,乙队员选拔赛成绩的中位数是 环;
(2)求甲队员10次射击成绩的平均数和方差,根据甲、乙两名队员的选拔赛成绩,你推荐谁代表学校参加比赛,并说明理由;
(3)为提升射击队技战术水平,学校决定除甲、乙外,再从射击队其他4名队员(三名男生,一名女生)中随机选出两名队员一同前往观看比赛,用列表或画树形图的方法求出恰好选出一名男生利一名女生的概率.
19.(8分)小邕做数学题时遇到了如下问题:如图1,△ABD是⊙O的内接三角形,直线l经过点A,点E是直线l上的一点且∠ABD=∠DAE.求证:直线l是⊙O的切线.小邕添加了适当的辅助线后,得到了图2的图形,并利用它解决了问题.
(1)请你根据小邕的思考,写出解决这一问题的过程;
(2)在图3中,作直径BC,连接CD,得到图3.若∠DAE=30°,AD=2,AB=8,求CD的长.
20.(8分)某商家销售一种糕点,每盒进价为40元.在销售过程中发现,周销量y(盒)与销售单价x(元)之间满足一次函数关系,其部分对应数据如表所示:
销售单价x(元) … 60 65 70 …
周销量y(盒) … 240 210 180 …
(1)求y关于x的函数表达式.
(2)当销售单价定为多少元时,每周出售这种糕点所获利润最大?最大利润为多少元?
(3)若规定销售单价需满足50≤x≤80,则每周至少可获得多少利润?
21.(9分)在矩形ABCD中,AB=4,BC=2,动点P从A出发,以1个单位每秒速度,沿射线AB方向运动,同时,动点Q从点C出发,以2个单位每秒速度,沿射线BC方向运动,设运动时间为t秒,连结DP,DQ.
(1)如图1.证明:DP⊥DQ.
(2)作∠PDQ平分线交直线BC于点E;
①图2,当点E与点B重合时,求t的值.
②连结PE,PQ,当△PBE与△PDQ相似时,求t的值.
22.(10分)如图,抛物线y=ax2+bx﹣6与x轴交于点A(﹣6,0)和点B(2,0).与y轴交于点C,连接AC,BC.
(1)求该抛物线的函数解析式.
(2)点P是直线AC下方抛物线上的一个动点,过点P作BC的平行线l,交线段AC于D.
①试探究:在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,求出点E的坐标;若不存在,请说明理由;
②设抛物线的对称轴与直线l交于点M,与直线AC交于点N.当S△DMN=S△AOC时,请直接写出DM的长.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:2的相反数是﹣2.
选:C.
2.解:从图1的左面看到的图形与图2相同,因此图2可能是它的左视图,B正确.
选:B.
3.解:139000000000=1.39×1011.
选:D.
4.解:由题意可得六边形ABCDEF是⊙O的内接正六边形,
所以六边形的内角和为(6﹣2)×180°=720°,
选:A.
5.解:∵△ABC≌△A′B′C′,∠C'=30°,
∴∠C=∠C′=30°,
在△ABC中,∠A=50°,∠C=30°,
∴∠B=180°﹣(∠A+∠C)=180°﹣(50°+30°)=100°;
选:D.
6.解:A、2a与3a2不是同类项,不能合并,此选项不符合题意;
B、(﹣3a)2=9a2,此选项不符合题意;
C、2(a﹣b)=2a﹣2b,此选项不符合题意;
D、a2 a5=a7,此选项符合题意;
选:D.
7.解:∵Δ=b2﹣4ac=20222﹣4×(﹣1)×2035>0,
∴一元二次方程﹣x2+2022x+2035=0有两个不相等的实数根,
选:D.
8.解:将4只未闭合的开关从上到下分别记为A,B,C,D,
则闭合开关A和D或闭合开关B和D时,小灯泡发光.
列表如下:
A B C D
A (A,B) (A,C) (A,D)
B (B,A) (B,C) (B,D)
C (C,A) (C,B) (C,D)
D (D,A) (D,B) (D,C)
共有12种等可能的结果,其中使得小灯泡发光的结果有:(A,D),(B,D),(D,A),(D,B),共4种,
∴使得小灯泡发光的概率为.
选:B.
9.解:如图,过点F作FH⊥BC于点H.则四边形CDFH是矩形,设AE交BF于点J.
∵四边形ABCD是正方形,
∴AB=AD=CD=BC=6,∠ADE=90°,
由作图可知MN垂直平分AB,FG垂直平分线段AE,
∴MN是正方形ABCD的对称轴,
∴DE=EC=3,
在Rt△ADE中,AE3,
∴AJ=JE,
∵cos∠DAE,
∴,
∴AF,
∵∠DAE+∠AFJ=90°,∠HFG+∠AFJ=90°,
∴∠DAE=∠HFG,
∵∠ADE=∠FHG=90°,FH=CD=AD,
∴△ADE≌△FHG(ASA),
∴DE=GH=3,
∵AF=BH,
∴BG=BH=GH3,
∴四边形AFGB的面积()×6.
选:B.
10.解:∵△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∵四边形CDEF是边长为4的正方形,且边DG在直线BC上,
∴∠CDE=∠DCF=90°,DG=4cm,
当0≤x≤4时,如图,DE交AB于点H,
则△BDH为等腰直角三角形,
∴BD=DH=x cm,
∴y=S△BDH( cm2);
当4<x≤8时,如图,过A作AO⊥BC于点O,CF交AB于点M,DE交AC于点N,
则△BMG和△CDN为等腰三角形,AOBC=4cm,
∴GM=BG=BD﹣DG=(x﹣4)cm,DN=CD=BC﹣BD=(8﹣x)cm,
∴y=S△ABC﹣S△BCM﹣S△CDN(x﹣6)2+12;
当8<x≤12时,如图,CF交AC于点P,
则△CGP为等腰直角三角形,
∵CD=BD﹣BC=(x﹣8)cm,
∴PG=CG=DG﹣CD=(12﹣x)cm,
∴y=S△CGP.
综上,.
选:A.
二.填空题(共5小题,满分15分,每小题3分)
11.解:680000=6.8×105.
答案为:6.8×105.
12.解:∵a2﹣3a+1=0,
∴a2=3a﹣1,
∴
=8,
答案为:8.
13.解:添加条件DO=BO,
证明:∵AO=CO,DO=BO,
∴四边形ABCD为平行四边形,
答案为:DO=BO.
14.解:过抛物线L2的顶点D作CD∥x轴,与y轴交于点C,如图所示:
则四边形OCDA是矩形,
∵抛物线L1:y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1,0),与y轴交于点B(0,2),
∴OB=2,OA=1,
将抛物线L1向下平移两个单位长度得抛物线L2,则AD=OC=2,
由图可知,阴影部分的面积等于矩形OCDA的面积,
∴S阴影部分=S矩形OCDA=OA AD=1×2=2.
答案为:2.
15.解:∵△ABC和△ADE是等腰直角三角形,
∴ACABCB,ADAE,
∴.
∵∠BAC=∠EAD=45°,
∴∠BAE=∠CAD,
∴△BAE∽△CAD,①正确.
∵△BAE∽△CAD,
∴∠BEA=∠CDA.
∵∠PME=∠AMD,
∴△PME∽△AMD,
∴,
∴MP MD=MA ME,②正确.
由②得MP MD=MA ME,
∴.
∵∠PMA=∠EMD,
∴△PMA∽△EMD,
∴∠APD=∠AED=90°.
∵∠CAE=180°﹣∠BAC﹣∠EAD=90°,
∴∠APD=∠CAE.
∵∠APD=∠CAE,∠C是公共角,
∴△CAP∽△CMA,
∴,
∴AC2=CP CM.
∵ACCB,
∴2CB2=CP CM,③正确.
答案为:①②③.
三.解答题(共7小题,满分55分)
16.解:原式=4x2﹣4x+1﹣[(2x)2﹣1]
=4x2﹣4x+1﹣4x2+1
=2﹣4x,
当时,原式.
17.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C即为所求.
(3)由勾股定理得,AC,
∴点A经过的路径长是.
答案为:.
18.解:(1)甲的成绩中,7环与8环都出现了3次,次数最多,众数为7环与8环;
把乙队员选拔赛成绩按从小到大的顺序排列,中位数是第5、第6个数的平均数,
则乙队员选拔赛成绩的中位数是6.5(环);
答案为:7与8,6.5;
(2)推荐甲队代表学校参加比赛.理由如下:
甲队的平均数是(环),
甲队的方差是:;
∵8>7,1.6<3.4,
∴甲以代表学校参加比赛;
(3)列表如下:
男1 男2 男3 女
男1 (男1,男2) (男1,男3) (男1,女)
男2 (男2,男1) (男2,男3) (男2,女)
男3 (男3,男1) (男3,男2) (男3,女)
女 (女,男1) (女,男2) (女,男3)
共有12种等可能的情况数,其中恰好选出一名男生和一名女生的有6种,
则恰好选出一名男生和一名女生的概率是.
19.(1)证明:如图2,作直径AF,连接DF,
则∠ADF=90°,
∴∠DAF+∠AFD=90°,
由圆周角定理得:∠ABD=∠AFD,
∵∠ABD=∠DAE,
∴∠DAE=∠AFD,
∴∠DAF+∠DAE=90°,
∴∠FAE=90°,
∵AF是⊙O的直径,
∴直线l是⊙O的切线;
(2)解:如图3,过点A作AH⊥BD于H,
∵∠DAE=30°,∠ABD=∠DAE,
∴∠ABD=∠DAE=30°,AF=2AD=4,
∴AHAB=4,BHAB=4,
由勾股定理得:DH2,
∴BD=BH+DH=6,
∴CD2.
20.解:(1)由题意,设y关于x的函数表达式为y=kx+b,
∴.
∴.
∴y关于x的函数表达式为y=﹣6x+600.
(2)由题意,可得每周出售这种糕点所获利润=(x﹣40)(﹣6x+600)
=﹣6x2+840x﹣24000
=﹣6(x﹣70)2+5400.
∵﹣6<0,
∴当x=70时,每周出售这种糕点所获利润最大,最大利润为5400元.
(3)由(2)每周出售这种糕点所获利润=﹣6(x﹣70)2+5400.
又∵50≤x≤80,
∴当x=50时,所获利润最小为3000元;当x=70时,所获利润最大为5400元.
∴销售单价需满足50≤x≤80,则每周至少可获得3000元的利润.
21.(1)证明:∵四边形ABCD是矩形,AB=4,BC=2,
∴∠A=∠DCQ=∠ADC=90°,
∴∠ADP+∠CDP=90°,
∵AB=CD=4,BC=AD=2,
∵AP=t,CQ=2t,
∴,
∴△ADP∽△CDQ,
∴∠ADP=∠CDQ,
∴∠CDQ+∠CDP=90°,即∠PDQ=90°,
∴DP⊥DQ;
(2)①解:∵DB平分∠PDQ,
∴∠PDB=∠BDQ=45°,
过点P作PF⊥BD交于点F,
∴PF=DF,
∵AP=t,AD=2,
∴DP,
∴PF,
∵sin∠ABD,
解得t或t=﹣6(舍);
②解:当P与A点重合时,△PBE≌△QDP,t=0;
以B为坐标原点,BC所在的直线为x轴,AB所在的直线为y轴,建立了直角坐标系,
∵AB=6,BC=2,
∴A(0,6),B(2,0),
∴D(2,6),
∵AP=t,CQ=2t,
∴P(0,4﹣t),Q(2+2t,0),
取DQ的中点M,连接EM,
∴M(2+t,2),
∵DE平分∠PDQ,
∴∠PDE=∠QDE,
∵CD=2AD,CQ=2AP,∠PDQ=90°,
∴△ADP∽△CDQ,
∴DQ=2AP,
∴DM=PD,
∴△PDE≌△MDE(SAS),
∴EP=EM,
当E点在C点左侧时,如图3﹣1﹣1,此时△PBE∽△QDP,
∴PB=BE,
∵PB=4﹣t,
∴BE=2t,
∴E(2t,0),
∴(4﹣t)2+(2t)2=(2t﹣2﹣t)2+4,
解得t=﹣5或t=﹣5(舍);
当E点在C点右侧,P点在BC上方时,如图3﹣2,△PBE∽△PDQ,
此时E(8﹣2t,0),
∴(6﹣3t)2+4=(4﹣t)2+(8﹣2t)2,
解得t或t(舍);
当E点在C点右侧,P点在BC下方时,如图3﹣3,△PBE∽△PDQ,
此时E(2t﹣8,0),P(4﹣t,0),
∴(4﹣t)2+(8﹣2t)2=(t﹣10)2+4,
解得t=1(舍)或t=6;
当E点在C点右侧,P点在BC下方时,如图3﹣4,△PBE∽△QDP,
此时E(t﹣2,0),P(4﹣t,0),
∴(4﹣t)2+(t﹣2)2=(t+4)2+4,
解得t=0(舍)或t=14;
综上所述:t的值为0或6或14或或﹣5.
22.解:(1)把点A(﹣6,0)和点B(2,0)代入抛物线y=ax2+bx﹣6得,
解得,
∴抛物线的函数解析式yx2+2x﹣6;
(2)①存在:
∵抛物线的函数解析式yx2+2x﹣6交y轴于C,
∴C(0,﹣6),
∵A(﹣6,0),
∴直线AC的解析式为y=﹣x﹣6,
设点D的坐标为(m,﹣m﹣6),其中﹣6<m<0,
∵B(2,0),C(0,﹣6),
∴BD2=(m﹣2)2+(m+6)2,BC2=22+62=40,DC2=m2+(﹣m﹣6+6)2=2m2,
∵DE∥BC,
∴当DE=BC时,以点D,C,B,E为顶点的四边形为平行四边形,
分两种情况:
如图,当BD=BC时,四边形BDEC为菱形,
∴BD2=BC2,
∴(m﹣2)2+(m+6)2=40,
解得:m1=﹣4,m2=0(舍去),
∴点D的坐标为(﹣4,﹣2),
∵点D向左移动2各单位长度,向下移动6个单位长度得到点E,
∴点E的坐标为(﹣6,﹣8);
如图,当CD=CB时,四边形CBED为菱形,
∴CD2=CB2,
∴2m2=40,
解得:m1=﹣2,m2=2(舍去),
∴点D的坐标为(﹣2,26),
∵点D向右移动2个单位长度,向上移动6个单位长度得到点E,
∴点E的坐标为(2﹣2,2);
综上,存在点E,使得以点D,C,B,E为顶点的四边形为菱形,点E的坐标为(﹣6,﹣8)或(2﹣2,2);
②设点D的坐标为(m,﹣m﹣6),其中﹣6<m<0,
∵A(﹣6,0),B(2,0),
∴抛物线的对称轴为直线x=﹣2,
∵直线BC的函数表达式为y=3x﹣6,直线l∥BC,
∴设直线l的解析式为y=3x+b,
∵点D的坐标(m,﹣m﹣6),
∴b=﹣4m﹣6,
∴M(﹣2,﹣4m﹣12),
∵抛物线的对称轴与直线AC交于点N,
∴N(﹣2,﹣4),
∴MN=﹣4m﹣12+4=﹣4m﹣8,
∵S△DMN=S△AOC,
∴(﹣4m﹣8)(﹣2﹣m)6×6,
整理得:m2+4m﹣5=0,
解得:m1=﹣5,m2=1(舍去),
∴点D的坐标为(﹣5,﹣1),
∴点M的坐标为(﹣2,8),
∴DM3,
答:DM的长为3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
