3.1.1 条件概率 课件(共15张PPT) 2024-2025学年湘教版(2019)高中数学选择性必修第二册
文档属性
| 名称 | 3.1.1 条件概率 课件(共15张PPT) 2024-2025学年湘教版(2019)高中数学选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 224.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 10:30:50 | ||
图片预览






文档简介
(共15张PPT)
3.1.1 条件概率
1.结合古典概型,了解条件概率,能计算简单随机事件的条件概率.
已知某班级中,有女生16人,男生14人,而且女生中喜欢长跑的有10人,男生中喜欢长跑的有8人.现从这个班级中随机抽出一名学生:
(1)求所抽到的学生喜欢长跑的概率;
(2)若已知抽到的是男生,求所抽到的学生喜欢长跑的概率.
思考:借助古典概型来处理,那么问题(1)中样本空间由什么组成?所抽到的学生喜欢长跑有几个样本点?其概率为多少?
样本空间Ω是由班级中所有学生组成的集合,共包含14+16=30个样本点.
记A:“所抽到的学生喜欢长跑”,其中包含10+8=18个样本点;
所抽到的学生喜欢长跑的概率为:
思考:借助古典概型来处理,那么问题(1)中样本空间由什么组成?所抽到的学生喜欢长跑有几个样本点?其概率为多少?
讨论:问题(2)中存在哪几个事件?事件之间有什么联系?如何求解问题(2)?
记A:“所抽到的学生喜欢长跑”, B:“抽到的学生是男生”,
已知抽到的是男生,求所抽到的学生喜欢长跑的概率即在事件B发生的条件下求事件A发生的概率.
其中样本空间Ω1是由班级中所有男生组成的集合,共包含14个样本点,事件AB(即)包含8个样本点.
因此,已知抽到的是男生,所抽到的学生喜欢长跑的概率为 .
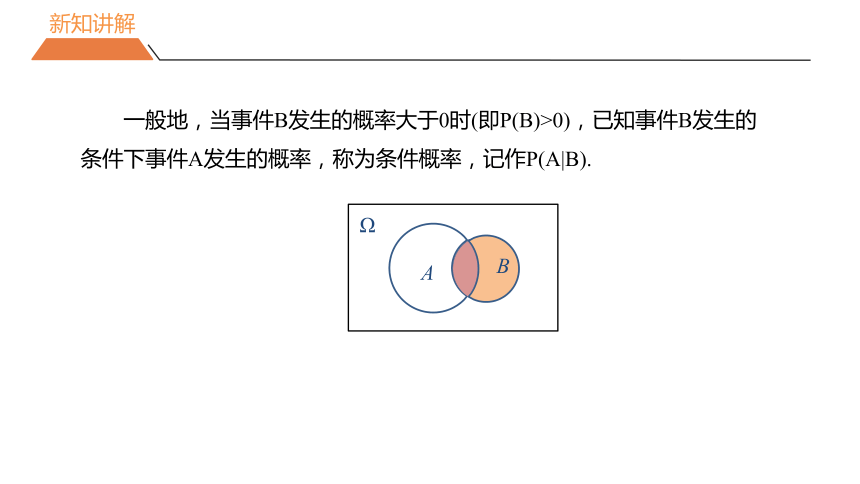
一般地,当事件B发生的概率大于0时(即P(B)>0),已知事件B发生的条件下事件A发生的概率,称为条件概率,记作P(A|B).
A
B
Ω
例1 某校高中三个年级各派一名男生和一名女生参加市里的中学生运动会 ,每人参加一个不同的项目,且每人能否获得冠军是等可能的.已知只有一名女生获得冠军,求高一女生获得冠军的概率.
解:设A=“一名女生获得冠军”,B=“高一女生获得冠军”,
已知A发生的条件下,A成为试验的样本空间,A中样本点具有等可能性,B是A的子集,A中样本点个数为3,B中样本点个数为1.
因此 .
例1中因为 所以 .
例2 从一副扑克的52张牌(去掉两张王牌后)中任取1张,求抽到梅花的条件下,抽到的是梅花5的概率.
解 设A=“抽到梅花”,B=“抽到梅花5”. 已知A发生的条件下,A成为试验的样本空间,A中的样本点具有等可能性,B是 A的子集,
因此 .
例2中因为 所以也有 .
条件概率计算公式:
归纳总结
我们可以借助下图来理解上述计算公式.
若已知事件 A 发生,则 A 成为样本空间.此时,事件 B 发生的概率是 AB 包含的样本点数与 A 包含的样本点数的比值,即
因为
所以,在事件 A 发生的条件下事件 B 发生的概率还可以通过 来计算.
问题1. 如何判断条件概率
题目中出现“在已知……前提下(或条件下)”“在A发生的条件下”等关键词,表明这个前提已成立或条件已发生,此时通常涉及条件概率.
问题2. P(B|A)与P(A|B)的区别是什么
P(B|A)表示在事件A发生的条件下,B发生的概率.
P(A|B)表示在事件B发生的条件下,A发生的概率.
例3 有圆形零件100个,其中有98 个直径合格,有96个光洁度合格,两个 指标都合格的有94个.从这100个零件中 任意抽取1个 .
(1)如果此零件光洁度合格,求直径也合格的概率(结果保留三位小数);
(2)如果此零件直径合格,求光洁度合格的概率(结果保留三位小数)
解:设A={直径合格},B={光洁度合格},则
(1)在光洁度合格的条件下直径也合格的概率是
(2)在直径合格的条件下光洁度也合格的概率是
归纳总结
用定义求条件概率的一般步骤:
1.某班有6名班干部,其中4名男生,2名女生.从中选出3人参加学校组织的社会实践活动,在男生甲被选中的情况下,女生乙也被选中的概率为( )
A. B. C. D.
2.抛掷骰子2次,每次结果用表示,其中分别表示第一次、第二次骰子的点数.若设,则________.
B
1. 条件概率的定义.
2. 条件概率的计算方法.
(古典概型)
(一般概型)
3. 求解条件概率的一般步骤
用字母表示有关事件
求相关量
代入公式求P(B|A)
3.1.1 条件概率
1.结合古典概型,了解条件概率,能计算简单随机事件的条件概率.
已知某班级中,有女生16人,男生14人,而且女生中喜欢长跑的有10人,男生中喜欢长跑的有8人.现从这个班级中随机抽出一名学生:
(1)求所抽到的学生喜欢长跑的概率;
(2)若已知抽到的是男生,求所抽到的学生喜欢长跑的概率.
思考:借助古典概型来处理,那么问题(1)中样本空间由什么组成?所抽到的学生喜欢长跑有几个样本点?其概率为多少?
样本空间Ω是由班级中所有学生组成的集合,共包含14+16=30个样本点.
记A:“所抽到的学生喜欢长跑”,其中包含10+8=18个样本点;
所抽到的学生喜欢长跑的概率为:
思考:借助古典概型来处理,那么问题(1)中样本空间由什么组成?所抽到的学生喜欢长跑有几个样本点?其概率为多少?
讨论:问题(2)中存在哪几个事件?事件之间有什么联系?如何求解问题(2)?
记A:“所抽到的学生喜欢长跑”, B:“抽到的学生是男生”,
已知抽到的是男生,求所抽到的学生喜欢长跑的概率即在事件B发生的条件下求事件A发生的概率.
其中样本空间Ω1是由班级中所有男生组成的集合,共包含14个样本点,事件AB(即)包含8个样本点.
因此,已知抽到的是男生,所抽到的学生喜欢长跑的概率为 .
一般地,当事件B发生的概率大于0时(即P(B)>0),已知事件B发生的条件下事件A发生的概率,称为条件概率,记作P(A|B).
A
B
Ω
例1 某校高中三个年级各派一名男生和一名女生参加市里的中学生运动会 ,每人参加一个不同的项目,且每人能否获得冠军是等可能的.已知只有一名女生获得冠军,求高一女生获得冠军的概率.
解:设A=“一名女生获得冠军”,B=“高一女生获得冠军”,
已知A发生的条件下,A成为试验的样本空间,A中样本点具有等可能性,B是A的子集,A中样本点个数为3,B中样本点个数为1.
因此 .
例1中因为 所以 .
例2 从一副扑克的52张牌(去掉两张王牌后)中任取1张,求抽到梅花的条件下,抽到的是梅花5的概率.
解 设A=“抽到梅花”,B=“抽到梅花5”. 已知A发生的条件下,A成为试验的样本空间,A中的样本点具有等可能性,B是 A的子集,
因此 .
例2中因为 所以也有 .
条件概率计算公式:
归纳总结
我们可以借助下图来理解上述计算公式.
若已知事件 A 发生,则 A 成为样本空间.此时,事件 B 发生的概率是 AB 包含的样本点数与 A 包含的样本点数的比值,即
因为
所以,在事件 A 发生的条件下事件 B 发生的概率还可以通过 来计算.
问题1. 如何判断条件概率
题目中出现“在已知……前提下(或条件下)”“在A发生的条件下”等关键词,表明这个前提已成立或条件已发生,此时通常涉及条件概率.
问题2. P(B|A)与P(A|B)的区别是什么
P(B|A)表示在事件A发生的条件下,B发生的概率.
P(A|B)表示在事件B发生的条件下,A发生的概率.
例3 有圆形零件100个,其中有98 个直径合格,有96个光洁度合格,两个 指标都合格的有94个.从这100个零件中 任意抽取1个 .
(1)如果此零件光洁度合格,求直径也合格的概率(结果保留三位小数);
(2)如果此零件直径合格,求光洁度合格的概率(结果保留三位小数)
解:设A={直径合格},B={光洁度合格},则
(1)在光洁度合格的条件下直径也合格的概率是
(2)在直径合格的条件下光洁度也合格的概率是
归纳总结
用定义求条件概率的一般步骤:
1.某班有6名班干部,其中4名男生,2名女生.从中选出3人参加学校组织的社会实践活动,在男生甲被选中的情况下,女生乙也被选中的概率为( )
A. B. C. D.
2.抛掷骰子2次,每次结果用表示,其中分别表示第一次、第二次骰子的点数.若设,则________.
B
1. 条件概率的定义.
2. 条件概率的计算方法.
(古典概型)
(一般概型)
3. 求解条件概率的一般步骤
用字母表示有关事件
求相关量
代入公式求P(B|A)
同课章节目录
