3.2.1 离散型随机变量及其分布 课件(共20张PPT) 2024-2025学年湘教版(2019)高中数学选择性必修第二册
文档属性
| 名称 | 3.2.1 离散型随机变量及其分布 课件(共20张PPT) 2024-2025学年湘教版(2019)高中数学选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 772.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 10:32:08 | ||
图片预览






文档简介
(共20张PPT)
3.2.1 离散型随机变量及其分布
1.通过具体实例,了解随机变量,离散型随机变量的概念.
2.理解随机变量的分布列,会求一些离散型随机变量的分布列.
1.掷一枚骰子,出现的点数可能为 .
{1,2,3,4,5,6}
2.掷一枚硬币,可能会出现哪几种结果?
{正面向上,反面向上}
随机变量的概念
一般地,如果随机试验的样本空间为Ω,而且对于Ω中的每一个样本点,变量X都对应有唯一确定的实数值,就称X为一个随机变量.
表示:
①大写英文字母X,Y,Z,…
②小写希腊字母ξ,η,ζ,…
取值范围:随机变量所有可能的取值组成的集合.
如果随机变量X的所有取值都可以逐个列举出来,则称X为离散型随机变量.
例1 (多选)下面给出四个随机变量,其中是离散型随机变量的是( )
A.某高速公路上某收费站在未来1小时内经过的车辆数X是一个随机变量
B.一个沿直线y=x进行随机运动的质点,它在该直线上的位置Y是一个随机变量
C.某网站未来1小时内的点击量
D.一天内的温度η
AC
归纳总结
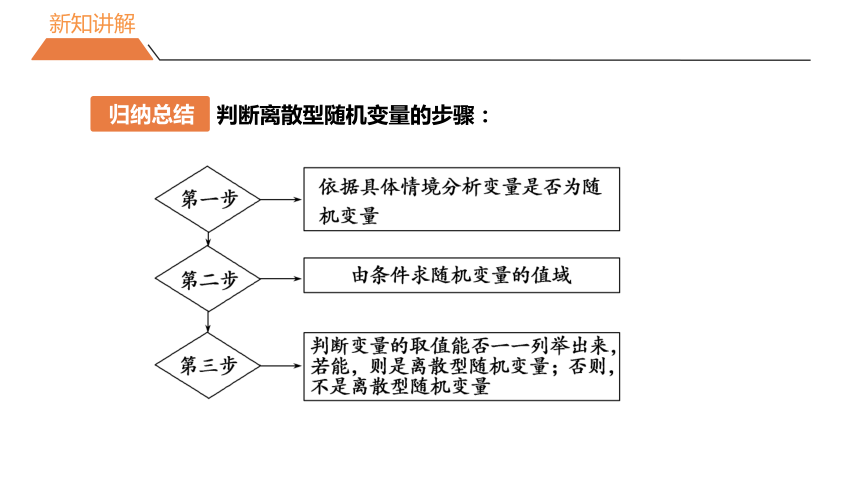
判断离散型随机变量的步骤:
在课堂提问环节,四川汶川的一位小学生向航天员提问了4个问题,记王亚平老师回答问题个数为随机变量X.
问题1:随机变量X的取值是 .
问题2:设王亚平老师回答每个问题的概率是P(X=0)=0.1,P(X=1)=0.3,P(X=2)=0.4,P(X=3)=0.1,P(X=4)=0.1,求出P(-1≤X≤1),P(1≤X≤3),P(0≤X≤4)的值?
问题3:如果是给定的实数,则P(a≤X≤b)一定可以算出来吗?
问题4:对于问题2中的随机变量和对应的概率有没有更直观的表示方法.
0,1,2,3,4
0.4
0.8
P(0≤X≤4)=1
X 0 1 2 3 4
P 0.1 0.3 0.4 0.1 0.1
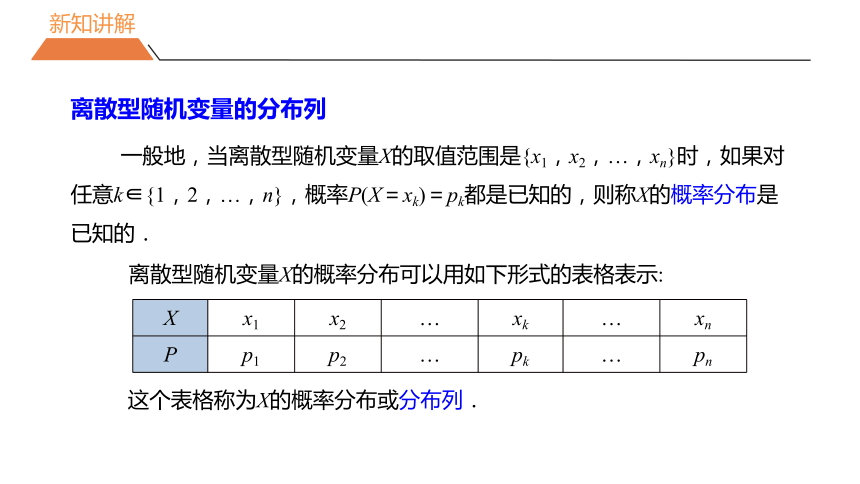
一般地,当离散型随机变量X的取值范围是{x1,x2,…,xn}时,如果对任意k∈{1,2,…,n},概率P(X=xk)=pk都是已知的,则称X的概率分布是已知的.
离散型随机变量X的概率分布可以用如下形式的表格表示:
X x1 x2 … xk … xn
P p1 p2 … pk … pn
离散型随机变量的分布列
这个表格称为X的概率分布或分布列.
例2 抛掷一枚质地均匀的骰子,用X表示骰子向上一面的点数,那么
(1)所有随机事件X的取值范围是什么?
(2)求X的分布列.
(1)X的取值范围:{1,2,3,4,5,6};
X 1 2 3 4 5 6
P
(2)当X分别为1,2,3,4,5,6时,其概率相等,都为.
其分布列为
抛掷一枚质地均匀的骰子,用X表示骰子向上一面的点数,那么
(3)分布列中X=1与X=2对应的随机事件之间有什么关系?X=3与X=4呢?
彼此互斥;
必然事件.
随机变量X=1,2,3,4,5,6对应的概率之和为1.
Ω=(X=1)∪(X=2)∪(X=3)∪(X=4)∪(X=5)∪(X=6),
P(Ω)=P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)+P(X=6),
符号语言:
1=p1+p2+p3+p4+p5+p6
(4)X=1,2,3,4,5,6对应的随机事件的和事件是什么事件?从概率角度如何解释?
离散型随机变量的分布列必须满足:
离散型随机变量的分布列的性质
X x1 x2 … xk … xn
P p1 p2 … pk … pn
②
① pk≥0,k=1,2,…,n;
归纳总结
离散型随机变量的分布列还可以用图象来近似表示.
例如,在掷骰子实验中,得到的点数X的分布列的图象如图所示.
从图中可以看出,X的取值范围是{1,2,3,4,5,6},它取每个值的概率均为.
例3 某班有学生45人,其中O型血的有10人,A型血的有12人,B型血的有8人,AB型血的有15人.现从中抽1人,其血型为随机变量X,求X的分布列.
解:将O,A,B,AB四种血型分别编号为1,2,3,4,
则X的可能取值为1,2,3,4.
P(X=1)==,P(X=2)==,P(X=3)==,P(X=4)==.
故X的分布列为
X 1 2 3 4
P
求离散型随机变量分布列的一般步骤
归纳总结
例4 已知离散型随机变量X的分布列P(X=) =ak(k=1,2,3,4,5).
(1)求常数a的值;(2)求P(X≥);(3)求P(解:(1)由题意得随机变量X的分布列如下表所示.
由分布列的性质得,a+2a+3a+4a+5a=1,解得a=.
X 1
P a 2a 3a 4a 5a
(2)P=P+P+P==.
(3)∵∴P=P+P==.
X 1
P
离散型随机变量分布列的性质的三个应用:
归纳总结
1.先后抛掷一枚质地均匀的骰子5次,那么不能作为随机变量的是( )
A.出现7点的次数
B.出现偶数点的次数
C.出现2点的次数
D.出现的点数大于2小于6的次数
A
2.下列表格中,不是某个随机变量的分布列的是( )
A. B.
C. D.
C
X 0 1 2
P 0.7 0.15 0.15
X -2 0 2 4
P 0.5 0.2 0.3 0
X 1 2 3
P lg 1 lg 2 lg 5
随机变量
离散型随机变量的概念
离散型随机变量的分布列
概念
性质
3.2.1 离散型随机变量及其分布
1.通过具体实例,了解随机变量,离散型随机变量的概念.
2.理解随机变量的分布列,会求一些离散型随机变量的分布列.
1.掷一枚骰子,出现的点数可能为 .
{1,2,3,4,5,6}
2.掷一枚硬币,可能会出现哪几种结果?
{正面向上,反面向上}
随机变量的概念
一般地,如果随机试验的样本空间为Ω,而且对于Ω中的每一个样本点,变量X都对应有唯一确定的实数值,就称X为一个随机变量.
表示:
①大写英文字母X,Y,Z,…
②小写希腊字母ξ,η,ζ,…
取值范围:随机变量所有可能的取值组成的集合.
如果随机变量X的所有取值都可以逐个列举出来,则称X为离散型随机变量.
例1 (多选)下面给出四个随机变量,其中是离散型随机变量的是( )
A.某高速公路上某收费站在未来1小时内经过的车辆数X是一个随机变量
B.一个沿直线y=x进行随机运动的质点,它在该直线上的位置Y是一个随机变量
C.某网站未来1小时内的点击量
D.一天内的温度η
AC
归纳总结
判断离散型随机变量的步骤:
在课堂提问环节,四川汶川的一位小学生向航天员提问了4个问题,记王亚平老师回答问题个数为随机变量X.
问题1:随机变量X的取值是 .
问题2:设王亚平老师回答每个问题的概率是P(X=0)=0.1,P(X=1)=0.3,P(X=2)=0.4,P(X=3)=0.1,P(X=4)=0.1,求出P(-1≤X≤1),P(1≤X≤3),P(0≤X≤4)的值?
问题3:如果是给定的实数,则P(a≤X≤b)一定可以算出来吗?
问题4:对于问题2中的随机变量和对应的概率有没有更直观的表示方法.
0,1,2,3,4
0.4
0.8
P(0≤X≤4)=1
X 0 1 2 3 4
P 0.1 0.3 0.4 0.1 0.1
一般地,当离散型随机变量X的取值范围是{x1,x2,…,xn}时,如果对任意k∈{1,2,…,n},概率P(X=xk)=pk都是已知的,则称X的概率分布是已知的.
离散型随机变量X的概率分布可以用如下形式的表格表示:
X x1 x2 … xk … xn
P p1 p2 … pk … pn
离散型随机变量的分布列
这个表格称为X的概率分布或分布列.
例2 抛掷一枚质地均匀的骰子,用X表示骰子向上一面的点数,那么
(1)所有随机事件X的取值范围是什么?
(2)求X的分布列.
(1)X的取值范围:{1,2,3,4,5,6};
X 1 2 3 4 5 6
P
(2)当X分别为1,2,3,4,5,6时,其概率相等,都为.
其分布列为
抛掷一枚质地均匀的骰子,用X表示骰子向上一面的点数,那么
(3)分布列中X=1与X=2对应的随机事件之间有什么关系?X=3与X=4呢?
彼此互斥;
必然事件.
随机变量X=1,2,3,4,5,6对应的概率之和为1.
Ω=(X=1)∪(X=2)∪(X=3)∪(X=4)∪(X=5)∪(X=6),
P(Ω)=P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)+P(X=6),
符号语言:
1=p1+p2+p3+p4+p5+p6
(4)X=1,2,3,4,5,6对应的随机事件的和事件是什么事件?从概率角度如何解释?
离散型随机变量的分布列必须满足:
离散型随机变量的分布列的性质
X x1 x2 … xk … xn
P p1 p2 … pk … pn
②
① pk≥0,k=1,2,…,n;
归纳总结
离散型随机变量的分布列还可以用图象来近似表示.
例如,在掷骰子实验中,得到的点数X的分布列的图象如图所示.
从图中可以看出,X的取值范围是{1,2,3,4,5,6},它取每个值的概率均为.
例3 某班有学生45人,其中O型血的有10人,A型血的有12人,B型血的有8人,AB型血的有15人.现从中抽1人,其血型为随机变量X,求X的分布列.
解:将O,A,B,AB四种血型分别编号为1,2,3,4,
则X的可能取值为1,2,3,4.
P(X=1)==,P(X=2)==,P(X=3)==,P(X=4)==.
故X的分布列为
X 1 2 3 4
P
求离散型随机变量分布列的一般步骤
归纳总结
例4 已知离散型随机变量X的分布列P(X=) =ak(k=1,2,3,4,5).
(1)求常数a的值;(2)求P(X≥);(3)求P(
由分布列的性质得,a+2a+3a+4a+5a=1,解得a=.
X 1
P a 2a 3a 4a 5a
(2)P=P+P+P==.
(3)∵
X 1
P
离散型随机变量分布列的性质的三个应用:
归纳总结
1.先后抛掷一枚质地均匀的骰子5次,那么不能作为随机变量的是( )
A.出现7点的次数
B.出现偶数点的次数
C.出现2点的次数
D.出现的点数大于2小于6的次数
A
2.下列表格中,不是某个随机变量的分布列的是( )
A. B.
C. D.
C
X 0 1 2
P 0.7 0.15 0.15
X -2 0 2 4
P 0.5 0.2 0.3 0
X 1 2 3
P lg 1 lg 2 lg 5
随机变量
离散型随机变量的概念
离散型随机变量的分布列
概念
性质
同课章节目录
