3.2.3 离散型随机变量的数学期望 课件(共18张PPT) 2024-2025学年湘教版(2019)高中数学选择性必修第二册
文档属性
| 名称 | 3.2.3 离散型随机变量的数学期望 课件(共18张PPT) 2024-2025学年湘教版(2019)高中数学选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 10:32:45 | ||
图片预览






文档简介
(共18张PPT)
3.2.3 离散型随机变量的数学期望
1.通过具体实例,理解离散型随机变量的数学期望(均值).
2.掌握二项分布的均值,了解超几何分布的均值.
3.掌握离散型随机变量的数学期望(均值)的性质,能用数学期望(均值)解决一些简单的实际问题.
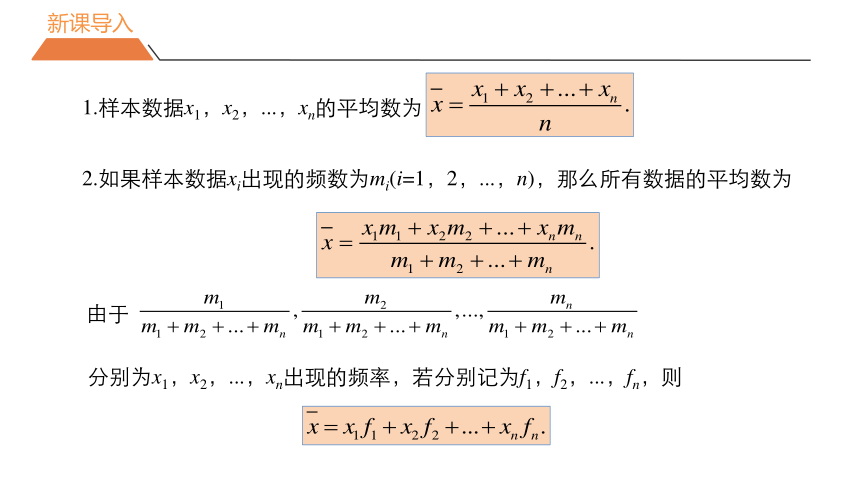
1.样本数据x1,x2,...,xn的平均数为
2.如果样本数据xi出现的频数为mi(i=1,2,...,n),那么所有数据的平均数为
分别为x1,x2,...,xn出现的频率,若分别记为f1,f2,...,fn,则
由于
情境:一家投资公司在决定是否对某创业项目进行资助时,经过评估后发现:如果项目成功,将获利5000万元;如果项目失败,将损失3000万元.
设这个项目成功的概率为p,而你是投资公司的负责人,如果仅从平均收益方面考虑,则p满足什么条件时,你才会对该项目进行资助?为什么
问题:1.如果重复这个创业项目n次,那么成功和失败的次数分别是多少?平均收益是多少?此时p满足什么条件时,你才会对该项目进行资助?
项目成功的概率为p,则成功次数估计为np,失败次数估计为n-np=n(1-p).
因此在这n次试验中,投资方收益(单位:万元)的n个数据可以估计为
这一组数的平均数为
因为上述平均数体现的是平均收益,所以当
5000p+(-3000)(1-p)>0,
即p>0.375时,就应该对创业项目进行资助.
2.设投资公司的收益为X,试列出随机变量X的分布列.你有什么发现?
随机变量X的分布列如下
X 5000 -3000
P p 1-p
从上面分析可知,式子5000p+(-3000)(1-p)刻画了X取值的平均水平.
离散型随机变量的数学期望
一般地,如果离散型随机变量X的分布列如下表所示.
X x1 x2 ... xk ... xn
P p1 p2 ... pk ... pn
则称
为离散型随机变量X的均值或数学期望(简称为期望)
说明:离散型随机变量X的均值E(X)也可以用EX表示,它刻画了X的平均取值.
例1 盒中装有5节同牌号的五号电池,其中混有两节废电池.现在无放回地每次取一节电池检验,直到取到好电池为止,求抽取次数X的分布列及均值.
解:(1)X的所有可能取值为1,2,3,则
抽取次数X的分布列为
X 1 2 3
P
所以
方法归纳
求离散型随机变量X的均值的步骤:
(1)确定随机变量X的所有可能的取值;
(2)求出随机变量取各个值时对应的概率;
(3)利用公式 求出均值.
思考:已知随机变量X服从参数为p的两点分布,求E(X).
解:随机变量X服从参数为p的两点分布,其分布列如下
X 1 0
P p 1-p
所以E(X)=1×p+0×(1-p)=p.
常见分布的均值
名称 两点分布 二项分布 X~B(n,p) 超几何分布
X~H(N,n,M)
公式 E(X)=p
E(X)=np
思考:若X,Y都是离散型随机变量,且Y=aX+b(其中a,b是常数),那么E(Y)与E(X)有怎样的关系?
分析:将白球和黑球视为“正品”,红球视为“次品”,则所求问题转化为100件产品中有5件次品,随机从中抽取20件产品,则取出次品件数5服从超几何分布.
例2 一袋中装有50个白球,45个黑球,5个红球,现从中随机抽取20个球,求取出的红球个数ξ的数学期望.
解:袋中球的总数为50+45+5=100,由已知可得ξ服从超几何分布,即ξ~(100,5,20),
∴随机变量ξ的数学期望E(ξ)=n=20×=1.
例3 体检时,为了确定体检人员是否患有某种疾病,需要对其血液进行化验,若结果呈阳性,则患有该疾病;若结果呈阴性,则未患有该疾病.已知每位体检人患有该疾病的概率均为0.1,化验结果不会出错,而且体检人是否患有该疾病相互独立.现有5位体检人的血液待检查,有以下两种化验方案:
方案甲:逐个检查每位体检人的血液;
方案乙:先将5位体检人的血液混在一起化验一次,若呈阳性,则再逐个化验;若呈阴性,则说明每位体检人均未患有该疾病,化验结束.
(1)哪种化验方案更好?
(2)如果每次化验的费用为100元,求方案乙的平均化验费用.
解:(1)方案甲中,化验的次数一定为5次.
方案乙中,若化验次数为X,则X的取值范围是{1,6},
因为5人都不患病的概率为(1-0.1)5=0.59049,
所以
P(X=1)=0.59049,
P(X=6)=1-0.59049=0.40951,
从而
E(X)=1×0.59049+6×0.40951=3.04755.
方案乙的平均检查次数不到5次,因此方案乙更好.
(2)如果每次化验的费用为100元,求方案乙的平均化验费用.
若记方案乙中,检查费用为Y元,则Y=100X,则
E(Y)=100E(X)=304.755.
即方案乙的平均化验费用为304.755元.
1.若随机变量X~B(6,),则数学期望E(X)=( )
A.6 B.3 C. D.
2.设ξ的分布列为
又设η=2ξ+5,则E(η)等于( )
ξ 1 2 3 4
P
A. B. C. D.
B
D
根据今天所学,回答下列问题:
1.求离散型随机变量均值的步骤分为哪几步?
2.离散型随机变量的均值有什么性质?
3.2.3 离散型随机变量的数学期望
1.通过具体实例,理解离散型随机变量的数学期望(均值).
2.掌握二项分布的均值,了解超几何分布的均值.
3.掌握离散型随机变量的数学期望(均值)的性质,能用数学期望(均值)解决一些简单的实际问题.
1.样本数据x1,x2,...,xn的平均数为
2.如果样本数据xi出现的频数为mi(i=1,2,...,n),那么所有数据的平均数为
分别为x1,x2,...,xn出现的频率,若分别记为f1,f2,...,fn,则
由于
情境:一家投资公司在决定是否对某创业项目进行资助时,经过评估后发现:如果项目成功,将获利5000万元;如果项目失败,将损失3000万元.
设这个项目成功的概率为p,而你是投资公司的负责人,如果仅从平均收益方面考虑,则p满足什么条件时,你才会对该项目进行资助?为什么
问题:1.如果重复这个创业项目n次,那么成功和失败的次数分别是多少?平均收益是多少?此时p满足什么条件时,你才会对该项目进行资助?
项目成功的概率为p,则成功次数估计为np,失败次数估计为n-np=n(1-p).
因此在这n次试验中,投资方收益(单位:万元)的n个数据可以估计为
这一组数的平均数为
因为上述平均数体现的是平均收益,所以当
5000p+(-3000)(1-p)>0,
即p>0.375时,就应该对创业项目进行资助.
2.设投资公司的收益为X,试列出随机变量X的分布列.你有什么发现?
随机变量X的分布列如下
X 5000 -3000
P p 1-p
从上面分析可知,式子5000p+(-3000)(1-p)刻画了X取值的平均水平.
离散型随机变量的数学期望
一般地,如果离散型随机变量X的分布列如下表所示.
X x1 x2 ... xk ... xn
P p1 p2 ... pk ... pn
则称
为离散型随机变量X的均值或数学期望(简称为期望)
说明:离散型随机变量X的均值E(X)也可以用EX表示,它刻画了X的平均取值.
例1 盒中装有5节同牌号的五号电池,其中混有两节废电池.现在无放回地每次取一节电池检验,直到取到好电池为止,求抽取次数X的分布列及均值.
解:(1)X的所有可能取值为1,2,3,则
抽取次数X的分布列为
X 1 2 3
P
所以
方法归纳
求离散型随机变量X的均值的步骤:
(1)确定随机变量X的所有可能的取值;
(2)求出随机变量取各个值时对应的概率;
(3)利用公式 求出均值.
思考:已知随机变量X服从参数为p的两点分布,求E(X).
解:随机变量X服从参数为p的两点分布,其分布列如下
X 1 0
P p 1-p
所以E(X)=1×p+0×(1-p)=p.
常见分布的均值
名称 两点分布 二项分布 X~B(n,p) 超几何分布
X~H(N,n,M)
公式 E(X)=p
E(X)=np
思考:若X,Y都是离散型随机变量,且Y=aX+b(其中a,b是常数),那么E(Y)与E(X)有怎样的关系?
分析:将白球和黑球视为“正品”,红球视为“次品”,则所求问题转化为100件产品中有5件次品,随机从中抽取20件产品,则取出次品件数5服从超几何分布.
例2 一袋中装有50个白球,45个黑球,5个红球,现从中随机抽取20个球,求取出的红球个数ξ的数学期望.
解:袋中球的总数为50+45+5=100,由已知可得ξ服从超几何分布,即ξ~(100,5,20),
∴随机变量ξ的数学期望E(ξ)=n=20×=1.
例3 体检时,为了确定体检人员是否患有某种疾病,需要对其血液进行化验,若结果呈阳性,则患有该疾病;若结果呈阴性,则未患有该疾病.已知每位体检人患有该疾病的概率均为0.1,化验结果不会出错,而且体检人是否患有该疾病相互独立.现有5位体检人的血液待检查,有以下两种化验方案:
方案甲:逐个检查每位体检人的血液;
方案乙:先将5位体检人的血液混在一起化验一次,若呈阳性,则再逐个化验;若呈阴性,则说明每位体检人均未患有该疾病,化验结束.
(1)哪种化验方案更好?
(2)如果每次化验的费用为100元,求方案乙的平均化验费用.
解:(1)方案甲中,化验的次数一定为5次.
方案乙中,若化验次数为X,则X的取值范围是{1,6},
因为5人都不患病的概率为(1-0.1)5=0.59049,
所以
P(X=1)=0.59049,
P(X=6)=1-0.59049=0.40951,
从而
E(X)=1×0.59049+6×0.40951=3.04755.
方案乙的平均检查次数不到5次,因此方案乙更好.
(2)如果每次化验的费用为100元,求方案乙的平均化验费用.
若记方案乙中,检查费用为Y元,则Y=100X,则
E(Y)=100E(X)=304.755.
即方案乙的平均化验费用为304.755元.
1.若随机变量X~B(6,),则数学期望E(X)=( )
A.6 B.3 C. D.
2.设ξ的分布列为
又设η=2ξ+5,则E(η)等于( )
ξ 1 2 3 4
P
A. B. C. D.
B
D
根据今天所学,回答下列问题:
1.求离散型随机变量均值的步骤分为哪几步?
2.离散型随机变量的均值有什么性质?
同课章节目录
