2025年山东泰安中考数学模拟测试题(含答案)
文档属性
| 名称 | 2025年山东泰安中考数学模拟测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 11:57:05 | ||
图片预览



文档简介
2025年山东泰安中考数学模拟测试题(含答案)
考试时间:120分钟;总分:150分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共12小题,满分48分,每小题4分)
1.(4分)若m的相反数是,则m的值为( )
A. B.﹣2023 C. D.2023
2.(4分)下列计算正确的是( )
A.x2 x3=x6
B.(﹣3x)2=6x2
C.8x4÷2x2=4x2
D.(x﹣2y)(x+2y)=x2﹣2y2
3.(4分)下列图形中,中心对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
4.(4分)据遵义市文化旅游局发布称:今年春节长假期间,遵义市累计实现旅游收入约为16.3亿元,数据16.3亿用科学记数法表示为( )
A.0.163×1010 B.1.63×1010
C.1.63×109 D.1.63×108
5.(4分)如图,已知直线m∥n,△ABC是等边三角形,顶点A在直线m上,顶点B在直线n上.若∠1=45°,则∠2的度数是( )
A.85° B.75° C.60° D.45°
6.(4分)如图,在⊙O内,若圆周角∠D=130°,则圆心角∠AOC的度数是( )
A.130° B.100° C.65° D.50°
7.(4分)已知方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值( )
A. k<﹣1 B.k>1 C. k<1且k≠0 D.k>﹣1且k≠0
8.(4分)小明买了两种不同的笔共8支,单价分别是1元和2元,共10元.设1元笔买了x支、2元笔买了y支,则可列方程组为( )
A. B.
C. D.
9.(4分)如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于D,下列三个结论:
①AD是∠BAC的平分线;
②∠ADC=60°;
③S△NCD:S△ACB=1:3.
其中正确的有( )
A.只有① B.只有①② C.只有①③ D.①②③
10.(4分)如图,这是一把2024年长寿区冬季运动会开幕式中一个表演节目的道具.它是以A为圆心,AB,AC为半径的扇形,其展开后夹角为120°,若AB的长为45cm,扇面BD的长为30cm,则展开后的扇面面积为( )
A.375πcm2 B.450πcm2 C.600πcm2 D.750πcm2
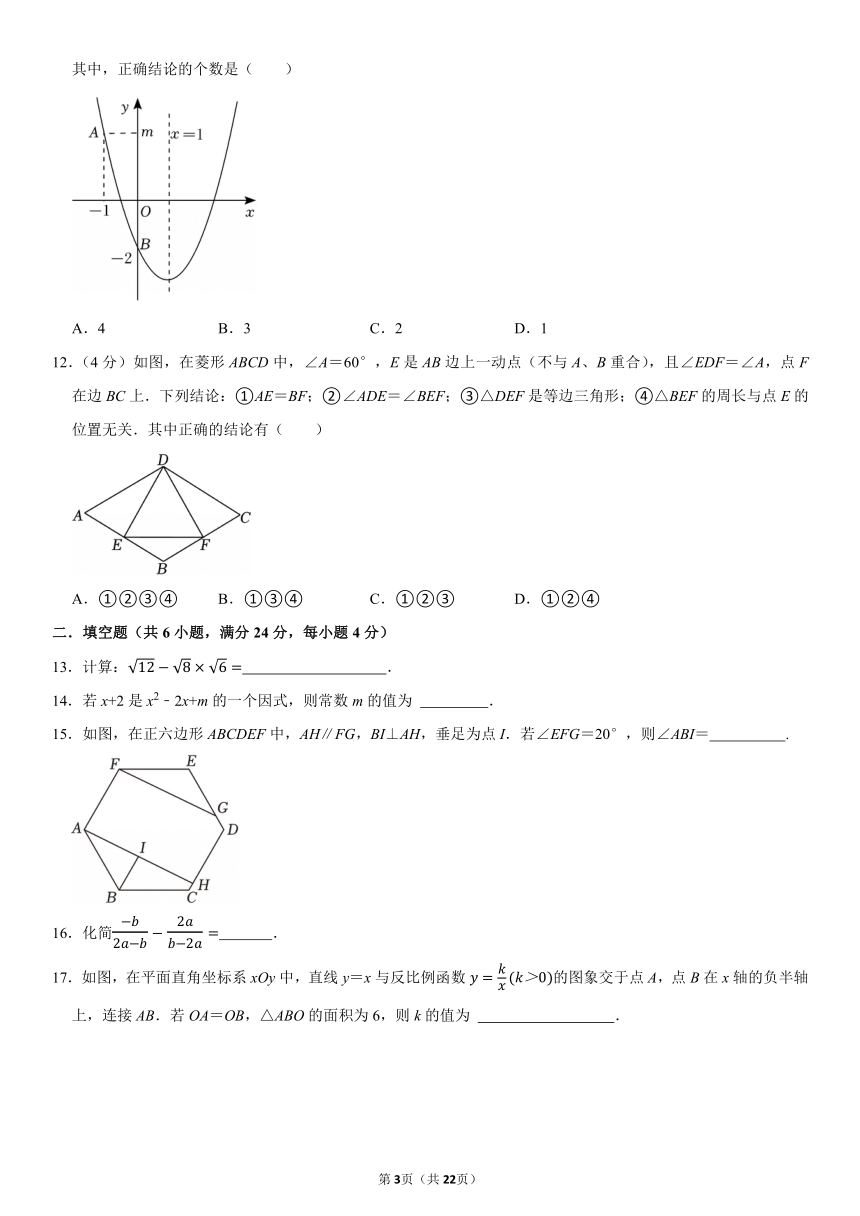
11.(4分)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与y轴交于点B(0,﹣2),点A(﹣1,m)在抛物线上,有下列结论:
①ab<0;
②一元二次方程ax2+bx+c=0的正实数根在2和3之间;
③;
④点P1(t,y1),P2(t+1,y2)在抛物线上,当实数时,y1<y2.
其中,正确结论的个数是( )
A.4 B.3 C.2 D.1
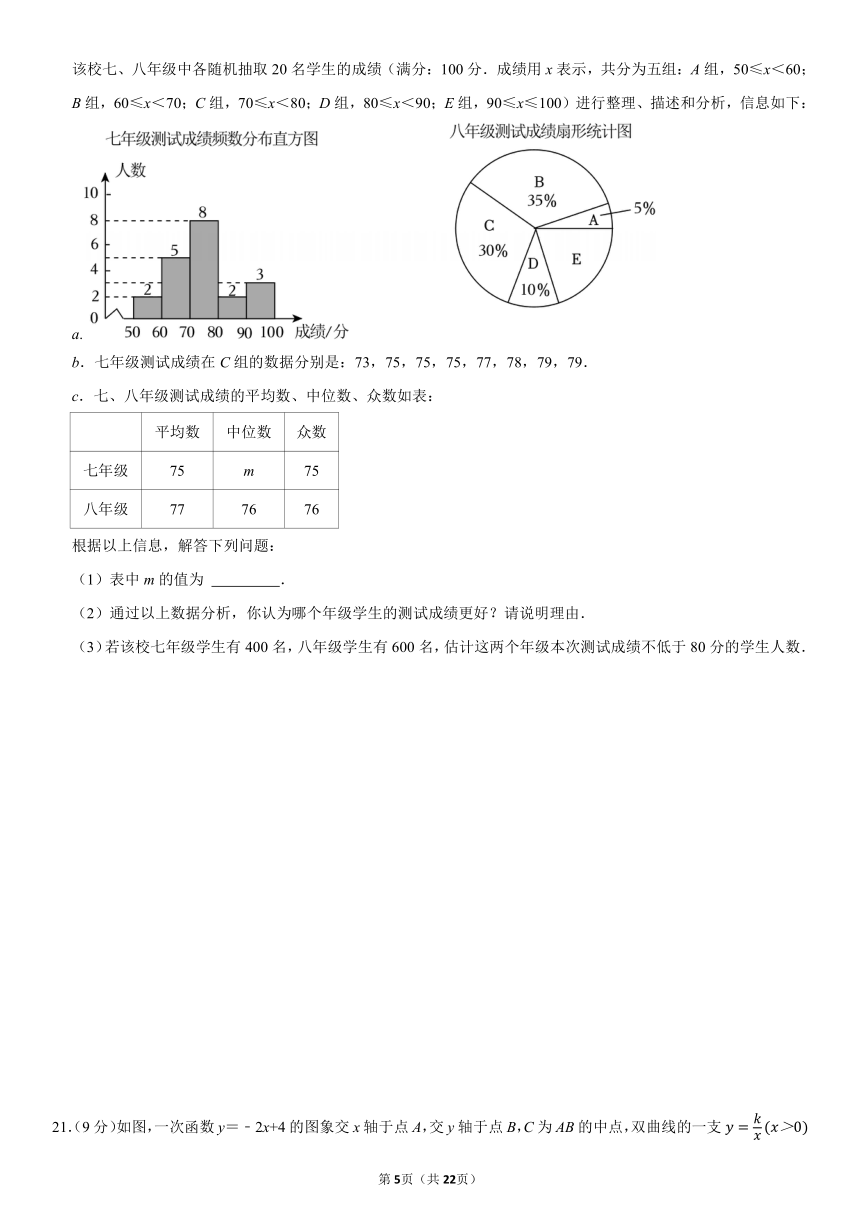
12.(4分)如图,在菱形ABCD中,∠A=60°,E是AB边上一动点(不与A、B重合),且∠EDF=∠A,点F在边BC上.下列结论:①AE=BF;②∠ADE=∠BEF;③△DEF是等边三角形;④△BEF的周长与点E的位置无关.其中正确的结论有( )
A.①②③④ B.①③④ C.①②③ D.①②④
二.填空题(共6小题,满分24分,每小题4分)
13.计算: .
14.若x+2是x2﹣2x+m的一个因式,则常数m的值为 .
15.如图,在正六边形ABCDEF中,AH∥FG,BI⊥AH,垂足为点I.若∠EFG=20°,则∠ABI= .
16.化简 .
17.如图,在平面直角坐标系xOy中,直线y=x与反比例函数的图象交于点A,点B在x轴的负半轴上,连接AB.若OA=OB,△ABO的面积为6,则k的值为 .
18.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形EFGH.若AB=4,BC=6,且AH<DH,则AH的长为 .
三.解答题(共7小题,满分78分)
19.(10分)计算
(1)
(2)
20.(11分)自2024年1月1日起,《未成年人网络保护条例》正式施行,这是我国出台的第一部专门性的未成年人网络保护综合立法.某校政教处组织七、八年级学生学习《未成年人网络保护条例》,并进行了相关知识测试.从该校七、八年级中各随机抽取20名学生的成绩(满分:100分.成绩用x表示,共分为五组:A组,50≤x<60;B组,60≤x<70;C组,70≤x<80;D组,80≤x<90;E组,90≤x≤100)进行整理、描述和分析,信息如下:
a.
b.七年级测试成绩在C组的数据分别是:73,75,75,75,77,78,79,79.
c.七、八年级测试成绩的平均数、中位数、众数如表:
平均数 中位数 众数
七年级 75 m 75
八年级 77 76 76
根据以上信息,解答下列问题:
(1)表中m的值为 .
(2)通过以上数据分析,你认为哪个年级学生的测试成绩更好?请说明理由.
(3)若该校七年级学生有400名,八年级学生有600名,估计这两个年级本次测试成绩不低于80分的学生人数.
21.(9分)如图,一次函数y=﹣2x+4的图象交x轴于点A,交y轴于点B,C为AB的中点,双曲线的一支过C,连接OC,将OC向右平移至PD,线段PD交于点E.
(1)求k的值;
(2)若PE:ED=1:3,求点E的坐标.
22.(10分)列分式方程解应用题:
节能降碳是积极稳妥推进碳达峰碳中和、全面推进美丽中国建设、促进经济社会发展全面绿色转型的重要举措.某公司积极响应节能降碳号召,决定采购新能源A型和B型两款汽车,已知每辆A型汽车的进价是每辆B型汽车的进价的1.5倍,若用1500万元购进A型汽车的数量比用1200万元购进B型汽车的数量少10辆.求A型和B型汽车的进价分别为每辆多少万元?
23.(12分)如图1,在正方形ABCD的BC边的延长线上取点G,以CG为边作正方形CGFE,连接AF,取AF的中点M,连接DM,EM.
(1)请说明线段DM,EM的关系,不必说理;
(2)如图2,把正方形CGFE绕点C顺时针旋转,当点G在BC上时,(1)中结论是否仍然成立?若成立,请说明理由;
(3)在旋转过程中,当D,E,F三点在一条直线上时,若AB=13,CE=5,请直接写出MF的长.
24.(13分)如图1,在等腰Rt△ABC中,∠ABC=90°,AB=CB,点D,E分别在AB,CB上,DB=EB,连结AE,CD,取AE中点F,连结BF.
(1)求证:CD=2BF,CD⊥BF;
(2)将△DBE绕点B顺时针旋转到图2的位置.
①请直接写出BF与CD的位置关系: ;
②求证:CD=2BF.
25.(13分)如图,抛物线y=ax2+3x+c与x轴交于A(﹣1,0),B两点,与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)P是第一象限内抛物线上的一点且横坐标为m.连接AP与BC相交于点Q,求的最大值;
(3)过点C作CM∥x轴交抛物线于点M,点E在x轴上,点N在抛物线上,是否存在点E和N,使∠MEN=90°,且EM=EN,若存在,求出点E的坐标,若不存在,请说明理由.
参考答案
一.选择题(共12小题,满分48分,每小题4分)
1.解:若m的相反数是,则m的值为.
选:A.
2.解:A.x2 x3=x5,A选项不符合题意;
B.(﹣3x)2=9x2,B不选项符合题意;
C.8x4÷2x2=4x2,C选项符合题意;
D.(x﹣2y)(x+2y)=x2﹣4y2,D选项不符合题意.
选:C.
3.解:第一个不是中心对称图形;
第二个是中心对称图形;
第三个是中心对称图形;
第四个是中心对称图形.
综上可得中心对称图形有3个.
选:C.
4.解:16.3亿=1630000000=1.63×109.
选:C.
5.解:∵m∥n,
∴∠3=∠1=45°.
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠2=180°﹣∠CAB﹣∠3=180°﹣60°﹣45°=75°.
选:B.
6.解:如图:
∵圆周角∠D=130°,
∴∠1=2∠D=260°,
∴∠AOC=360°﹣∠1=100°,
选:B.
7.解:根据题意得k≠0且Δ=22﹣4×k×(﹣1)>0,
所以k>﹣1且k≠0.
选:D.
8.解:设单价1元的笔买了x支,单价2元的笔买了y支,
由题意得:.
选:C.
9.解:由作法得AD平分∠BAC,所以①正确;
∴∠BAD=∠CAD,
∵∠C=90°,∠B=30°,
∴∠BAC=60°,
∴∠BAD=∠CAD=30°,
∴∠ADC=∠B+∠BAD=60°,所以②正确;
∵∠BAD=∠B,
∴DA=DB,
在Rt△ACD中,∵∠CAD=∠BAD=30°,
∴AD=2CD,
∴BD=2CD,
∴BC=3CD,
∴S△ACD:S△ABC=1:3,所以③错误.
选:B.
10.解:展开后的扇面面积S=S大扇形﹣S小扇形
=600π(cm2),
选:C.
11.解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x1,
∴b=﹣2a<0,
∴ab<0,所以结论①正确;
∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点坐标在(0,0)与(﹣1,0)之间,
∴抛物线与x轴的另一个交点坐标在(2,0)与(3,0)之间,
∴一元二次方程ax2+bx+c=0的正实数根在2和3之间,所以结论②正确;
把B(0,﹣2),A(﹣1,m)代入抛物线得c=﹣2,a﹣b+c=m,
而b=﹣2a,
∴a+2a﹣2=m,
∴,所以结论③正确;
∵点P1(t,y1),P2(t+1,y2)在抛物线上,
∴当点P1、P2都在直线x=1的右侧时,y1<y2,此时t≥1;
当点P1在直线x=1的左侧,点P2在直线x=1的右侧时,y1<y2,此时0<t<1且t+1﹣1>1﹣t,即t<1,
∴当t时,y1<y2,所以结论④错误.
选:B.
12.解:①连接BD,如图1所示:
∵四边形ABCD为菱形,∠A=60°,
∴AB=BC=CD=DA,∠A=∠C=60°,
∴△ABC和△BCD均为等边三角形,
∴AD=BD,∠ADB=∠ADE+∠EDB=60°,∠DBC=60°,
∴∠A=∠DBC=60°,
∵∠EDF=∠A=60°,
∴∠EDB+∠BDF=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,
,
∴△ADE≌△BDF(ASA),
∴AE=BF,DE=DF,
结论①正确;
②∵∠EDF=∠A=60°,DE=DF,
∴△DEF为等边三角形,
∴∠DEF=60°,
∴∠AED+∠BEF=120°,
∵∠A=60°,
∴∠AED+∠ADE=120°,
∴∠ADE=∠BEF,
结论②正确;
③由②可知:△DEF为等边三角形,
结论③正确;
④∵△DEF为等边三角形,
∴EF=DE,
∵AE=BF,
∴△BEF的周长=BE+BF+EF=BE+AE+EF=AB+DE,
∵点E在AB边上的位置不同,DE的长也不同,即DE的长随点E位置的变化而变化,
∴△BEF的周长=AB+DE也随点E位置的变化而变化,
即△BEF的周长与点E的位置有关,
结论④不正确,
综上所述:正确的结论是①②③.
选:C.
二.填空题(共6小题,满分24分,每小题4分)
13.解:原式
,
故答案为:.
14.解:设该多项式的另一个因式是x+n.
得(x+2)(x+n)=x2+(n+2)x+2n,
∴n+2=﹣2,
解得n=﹣4,
∴m=2n=2×(﹣4)=﹣8,
故答案为:﹣8.
15.解:∵六边形ABCDEF是正六边形,
∴∠AFE=∠BAF120°,
∵∠EFG=20°,
∴∠AFG=120°﹣20°=100°,
∵AH∥FG,
∴∠FAH=180°﹣100°=80°,
∴∠BAI=120°﹣80°=40°,
∵BI⊥AH,
∴∠ABI=90°﹣40°=50°,
故答案为:50°.
16.解:
=1.
故答案为:1.
17.解:作AD⊥x轴于点D,
∵直线y=x与反比例函数的图象交于点A,
∴设A(m,m),则AD=OD=m,k=m2,
∴OA,
∵OA=OB,
∴OB,
∵S△ABO6,
∴,
∴m2=6,
∴k=6,
故答案为:6.
18.解:作HP⊥BC于点P,则∠FPH=∠BPH=90°,
∵四边形ABCD是矩形,AB=4,BC=6,
∴∠A=∠B=∠C=90°,AD∥BC,
∴四边形ABPH是矩形,
∴PH=AB=4,AH=BP,
由折叠得∠EHJ=∠EHA∠AHF,∠GHK=∠GHD∠DHF,
∴∠EHG=∠EHJ+∠GHK(∠AHF+∠DHF)180°=90°,
同理∠FEH=∠GFE=90°,
∴四边形EFGH是矩形,
∴EH=GF,
∵∠EHJ=∠EHA∠AHF,∠GFK=∠GFC∠CFH,且∠AHF=∠CFH,
∴∠EHA=∠GFC,
在△EHA和△GFC中,
,
∴△EHA≌△GFC(AAS),
∴AH=CF,
∴BP=CF,
∵JH=AH=CF,JF=BF,
∴FH=JH+JF=CF+BF=BC=6,
∴PF2,
∴BP+CF=2AH=6﹣2,
∴AH=3,
故答案为:3.
三.解答题(共7小题,满分78分)
19.解:(1)原式
=2+1﹣1
=2;
(2)原式
=a﹣2.
20.解:(1)由题意得:m75.
答案为:75;
(2)八年级学生的测试成绩更好,理由如下:
因为八年级学生的测试成绩的平均数和中位数均高于七年级,所以八年级学生的测试成绩更好;
(3)400600×(1﹣5%﹣35%﹣30%)=100+180=280(人),
答:估计这两个年级本次测试成绩不低于80分的学生人数大约为280人.
21.解:(1)把x=0代入y=﹣2x+4得:
y=4,
∴点B的坐标为(0,4),
把y=0代入y=﹣2x+4得:
﹣2x+4=0,
解得:x=2,
∴点A的坐标为(2,0),
∵C为AB的中点,
∴点C的坐标为(1,2),
把(1,2)代入得:
k=1×2=2.
(2)过点E作EF⊥x轴于点F,过点D作DG⊥x轴于点G,如图所示:
∵将OC向右平移至PD,点C的坐标为(1,2),
∴DG=2,
∵PE:ED=1:3,
∴,
∵DG⊥x轴,EF⊥x轴,
∴EF∥DG,
∴△PEF∽△PDG,
∴,
∴,
∴E点的纵坐标为,
把代入得:
,
解得:x=4,
∴点E的坐标为.
22.解:设B型汽车的进价为每辆x万元,则A型汽车的进价为每辆1.5x万元,
依题意得10,
解得:x=20,
经检验,x=20是方程的解,1.5x=1.5×20=30,
答:A型汽车的进价为每辆30万元,B型汽车的进价为每辆20万元.
23.解:(1)DM=EM,DM⊥EM,理由如下:
如图,延长EM交AD于点K,
∵EF∥CG∥AD,
∴∠MAK=∠MFE,∠MKA=∠MEF,
∵M是AF的中点,
∴AM=FM,
∴△AMK≌△FME(AAS),
∴AK=EF=EC,KM=EM,
∵AD=CD,
∴AD﹣AK=CD﹣CE,即DK=DE,
∵∠KDE=90°,
∴△KDE是等腰直角三角形,
而KM=EM,
∴DM=EM,DM⊥EM.
(2)(1)中结论仍然成立,理由如下:
如图,延长EM,DA交于点T,
∵EF∥CG∥AD,
∴∠MAT=∠MFE,∠MTA=∠MEF,
∵M是AF的中点,
∴AM=FM,
∴△AMT≌△FME(AAS),
∴AT=EF=EC,TM=EM,
∵AD=CD,
∴AD+AT=CD+CE,即DT=DE,
∵∠TDE=90°,
∴△TDE是等腰直角三角形,
而TM=EM,
∴DM=EM,DM⊥EM.
(3)连接DE,过点M作MR⊥DE于点R,延长EM至H,使MH=ME,连接AH,DH,
当F在DC右侧时,如图,
∵MH=ME,∠AMH=∠EMF,AM=FM,
∴△AMH≌△FME(SAS),
∴AH=EF=EC,∠MAH=∠MFE,
∴AH∥DF,
∴∠DAH+∠ADE=180°,
∴∠DAH+∠CDE=90°,
∴∠DCE+∠CDE=90°,
∴∠DAH=∠DCE,
∵DA=DC,
∴△DAH≌△DCE(SAS),
∴DH=DE,∠ADH=∠CDE,
∴∠HDE=∠ADC=90°,
∵ME=MH,
∴DH⊥EH,DM=MH=EM,
在Rt△CDE中,DE,
∵DM=ME,DM⊥ME,MR⊥DE,
∴MRDE=6=DR=RE,
∴FR=EF+RE=11,
在Rt△RMF中,MF;
当F在DC左侧时,如图,
同法可得DE=12,MR=6=DR=RE,
∴FR=ER﹣FE=6﹣5=1,
在Rt△RMF中,MF,
综上,MF的长为或.
答:MF的长为或.
24.(1)证明:在△ABE和△CBD中,
∵AB=BC,∠ABE=∠CBD,BE=BD,
∴△ABE≌△CBD(SAS),
∴AE=CD,∠FAB=∠BCD.
∵F是Rt△ABE斜边AE的中点,
∴AE=2BF,
∴CD=2BF,
∵,
∴∠FAB=∠FBA.
∴∠FBA=∠BCD,
∵∠FBA+∠FBC=90°,
∴∠FBC+∠BCD=90°.
∴BF⊥CD;
(2)①BF⊥CD;
理由如下:延长BF到点G,使FG=BF,连结AG.延长EB到M,使BE=BM,连接AM并延长交CD于点N.
证△AGB≌△BDC(具体证法过程跟②一样).
∴∠ABG=∠BCD,
∵F是AE中点,B是EM中点,
∴BF是△ABM中位线,
∴BF∥AN,
∴∠ABG=∠BAN=∠BCD,
∴∠ABC=∠ANC=90°,
∴AN⊥CD,
∵BF∥AN,
∴BF⊥CD.
答案为:BF⊥CD;
②证明:延长BF到点G,使FG=BF,连结AG.
∵AF=EF,FG=BF,∠AFG=∠EFB,
∴△AGF≌△EBF(SAS),
∴∠FAG=∠FEB,AG=BE.
∴AG∥BE.
∴∠GAB+∠ABE=180°,
∵∠ABC=∠EBD=90°,
∴∠ABE+∠DBC=180°,
∴∠GAB=∠DBC.
∵BE=BD,
∴AG=BD.
在△AGB和△BDC中,
∵AG=BD,∠GAB=∠DBC,AB=CB,
∴△AGB≌△BDC(SAS),
∴CD=BG.
∵BG=2BF,
∴CD=2BF,
25.解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣x2+3x+4;
(2)令y=﹣x2+3x+4,则x=﹣1或4,
则点B(4,0),
过点A、P分别作y轴的平行线交BC于点N、H,
由点B、C的坐标得,直线BC的表达式为:y=﹣x+4,
当x=﹣1时,y=﹣x+4=5,即点N(﹣1,5),则AN=5,
设点P(x,﹣x2+3x+4),则点H(x,﹣x+4),
则PH=(﹣x2+3x+4)﹣(﹣x+4)=﹣x2+4x,
∵AN∥y轴∥PH,
则△AQN∽△PQH,
∴(x2﹣4x)(x﹣2)2,
即的最大值为;
(3)设E(t,0),当点E在点B的左侧时,若t<3,如图,
过点E作y轴的平行线交CM于点H,过点N作x轴的平行线交EH于点T,
∵∠HEM+∠HME=90°,∠HEM+∠NET=90°,
∴∠HEM=∠ENT,
∵∠EHM=∠NTE=90°,EM=EN,
∴△EHM≌△NTE(AAS),
∴HM=ET=3﹣t,HE=4=TN,
则点N(t+4,t﹣3),
将点N的坐标代入抛物线表达式得:t﹣3=﹣(t+4)2+3(t+4)+4,
解得:t=﹣3±2,
即点E的坐标为:(﹣3+2,0)或(﹣3﹣2,0);
若t=3时,如图,
当点N与点A重合时,EM=EN,∠MEN=90°,
∴E(3,0);
当点E在点B的右侧时,
同理可得,点N的坐标为:(t﹣4,3﹣t),
将点N的坐标代入抛物线表达式得:3﹣t=﹣(t﹣4)2+3(t﹣4)+4,
解得:t=3(舍去)或t=9,
∴E(9,0);
综上,点E的坐标为:(3+2,0)或(3﹣2,0)或(3,0)或(9,0).
第2页(共22页)
考试时间:120分钟;总分:150分
学校:___________姓名:___________班级:___________考号:___________
一.选择题(共12小题,满分48分,每小题4分)
1.(4分)若m的相反数是,则m的值为( )
A. B.﹣2023 C. D.2023
2.(4分)下列计算正确的是( )
A.x2 x3=x6
B.(﹣3x)2=6x2
C.8x4÷2x2=4x2
D.(x﹣2y)(x+2y)=x2﹣2y2
3.(4分)下列图形中,中心对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
4.(4分)据遵义市文化旅游局发布称:今年春节长假期间,遵义市累计实现旅游收入约为16.3亿元,数据16.3亿用科学记数法表示为( )
A.0.163×1010 B.1.63×1010
C.1.63×109 D.1.63×108
5.(4分)如图,已知直线m∥n,△ABC是等边三角形,顶点A在直线m上,顶点B在直线n上.若∠1=45°,则∠2的度数是( )
A.85° B.75° C.60° D.45°
6.(4分)如图,在⊙O内,若圆周角∠D=130°,则圆心角∠AOC的度数是( )
A.130° B.100° C.65° D.50°
7.(4分)已知方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值( )
A. k<﹣1 B.k>1 C. k<1且k≠0 D.k>﹣1且k≠0
8.(4分)小明买了两种不同的笔共8支,单价分别是1元和2元,共10元.设1元笔买了x支、2元笔买了y支,则可列方程组为( )
A. B.
C. D.
9.(4分)如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于D,下列三个结论:
①AD是∠BAC的平分线;
②∠ADC=60°;
③S△NCD:S△ACB=1:3.
其中正确的有( )
A.只有① B.只有①② C.只有①③ D.①②③
10.(4分)如图,这是一把2024年长寿区冬季运动会开幕式中一个表演节目的道具.它是以A为圆心,AB,AC为半径的扇形,其展开后夹角为120°,若AB的长为45cm,扇面BD的长为30cm,则展开后的扇面面积为( )
A.375πcm2 B.450πcm2 C.600πcm2 D.750πcm2
11.(4分)如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与y轴交于点B(0,﹣2),点A(﹣1,m)在抛物线上,有下列结论:
①ab<0;
②一元二次方程ax2+bx+c=0的正实数根在2和3之间;
③;
④点P1(t,y1),P2(t+1,y2)在抛物线上,当实数时,y1<y2.
其中,正确结论的个数是( )
A.4 B.3 C.2 D.1
12.(4分)如图,在菱形ABCD中,∠A=60°,E是AB边上一动点(不与A、B重合),且∠EDF=∠A,点F在边BC上.下列结论:①AE=BF;②∠ADE=∠BEF;③△DEF是等边三角形;④△BEF的周长与点E的位置无关.其中正确的结论有( )
A.①②③④ B.①③④ C.①②③ D.①②④
二.填空题(共6小题,满分24分,每小题4分)
13.计算: .
14.若x+2是x2﹣2x+m的一个因式,则常数m的值为 .
15.如图,在正六边形ABCDEF中,AH∥FG,BI⊥AH,垂足为点I.若∠EFG=20°,则∠ABI= .
16.化简 .
17.如图,在平面直角坐标系xOy中,直线y=x与反比例函数的图象交于点A,点B在x轴的负半轴上,连接AB.若OA=OB,△ABO的面积为6,则k的值为 .
18.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形EFGH.若AB=4,BC=6,且AH<DH,则AH的长为 .
三.解答题(共7小题,满分78分)
19.(10分)计算
(1)
(2)
20.(11分)自2024年1月1日起,《未成年人网络保护条例》正式施行,这是我国出台的第一部专门性的未成年人网络保护综合立法.某校政教处组织七、八年级学生学习《未成年人网络保护条例》,并进行了相关知识测试.从该校七、八年级中各随机抽取20名学生的成绩(满分:100分.成绩用x表示,共分为五组:A组,50≤x<60;B组,60≤x<70;C组,70≤x<80;D组,80≤x<90;E组,90≤x≤100)进行整理、描述和分析,信息如下:
a.
b.七年级测试成绩在C组的数据分别是:73,75,75,75,77,78,79,79.
c.七、八年级测试成绩的平均数、中位数、众数如表:
平均数 中位数 众数
七年级 75 m 75
八年级 77 76 76
根据以上信息,解答下列问题:
(1)表中m的值为 .
(2)通过以上数据分析,你认为哪个年级学生的测试成绩更好?请说明理由.
(3)若该校七年级学生有400名,八年级学生有600名,估计这两个年级本次测试成绩不低于80分的学生人数.
21.(9分)如图,一次函数y=﹣2x+4的图象交x轴于点A,交y轴于点B,C为AB的中点,双曲线的一支过C,连接OC,将OC向右平移至PD,线段PD交于点E.
(1)求k的值;
(2)若PE:ED=1:3,求点E的坐标.
22.(10分)列分式方程解应用题:
节能降碳是积极稳妥推进碳达峰碳中和、全面推进美丽中国建设、促进经济社会发展全面绿色转型的重要举措.某公司积极响应节能降碳号召,决定采购新能源A型和B型两款汽车,已知每辆A型汽车的进价是每辆B型汽车的进价的1.5倍,若用1500万元购进A型汽车的数量比用1200万元购进B型汽车的数量少10辆.求A型和B型汽车的进价分别为每辆多少万元?
23.(12分)如图1,在正方形ABCD的BC边的延长线上取点G,以CG为边作正方形CGFE,连接AF,取AF的中点M,连接DM,EM.
(1)请说明线段DM,EM的关系,不必说理;
(2)如图2,把正方形CGFE绕点C顺时针旋转,当点G在BC上时,(1)中结论是否仍然成立?若成立,请说明理由;
(3)在旋转过程中,当D,E,F三点在一条直线上时,若AB=13,CE=5,请直接写出MF的长.
24.(13分)如图1,在等腰Rt△ABC中,∠ABC=90°,AB=CB,点D,E分别在AB,CB上,DB=EB,连结AE,CD,取AE中点F,连结BF.
(1)求证:CD=2BF,CD⊥BF;
(2)将△DBE绕点B顺时针旋转到图2的位置.
①请直接写出BF与CD的位置关系: ;
②求证:CD=2BF.
25.(13分)如图,抛物线y=ax2+3x+c与x轴交于A(﹣1,0),B两点,与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)P是第一象限内抛物线上的一点且横坐标为m.连接AP与BC相交于点Q,求的最大值;
(3)过点C作CM∥x轴交抛物线于点M,点E在x轴上,点N在抛物线上,是否存在点E和N,使∠MEN=90°,且EM=EN,若存在,求出点E的坐标,若不存在,请说明理由.
参考答案
一.选择题(共12小题,满分48分,每小题4分)
1.解:若m的相反数是,则m的值为.
选:A.
2.解:A.x2 x3=x5,A选项不符合题意;
B.(﹣3x)2=9x2,B不选项符合题意;
C.8x4÷2x2=4x2,C选项符合题意;
D.(x﹣2y)(x+2y)=x2﹣4y2,D选项不符合题意.
选:C.
3.解:第一个不是中心对称图形;
第二个是中心对称图形;
第三个是中心对称图形;
第四个是中心对称图形.
综上可得中心对称图形有3个.
选:C.
4.解:16.3亿=1630000000=1.63×109.
选:C.
5.解:∵m∥n,
∴∠3=∠1=45°.
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠2=180°﹣∠CAB﹣∠3=180°﹣60°﹣45°=75°.
选:B.
6.解:如图:
∵圆周角∠D=130°,
∴∠1=2∠D=260°,
∴∠AOC=360°﹣∠1=100°,
选:B.
7.解:根据题意得k≠0且Δ=22﹣4×k×(﹣1)>0,
所以k>﹣1且k≠0.
选:D.
8.解:设单价1元的笔买了x支,单价2元的笔买了y支,
由题意得:.
选:C.
9.解:由作法得AD平分∠BAC,所以①正确;
∴∠BAD=∠CAD,
∵∠C=90°,∠B=30°,
∴∠BAC=60°,
∴∠BAD=∠CAD=30°,
∴∠ADC=∠B+∠BAD=60°,所以②正确;
∵∠BAD=∠B,
∴DA=DB,
在Rt△ACD中,∵∠CAD=∠BAD=30°,
∴AD=2CD,
∴BD=2CD,
∴BC=3CD,
∴S△ACD:S△ABC=1:3,所以③错误.
选:B.
10.解:展开后的扇面面积S=S大扇形﹣S小扇形
=600π(cm2),
选:C.
11.解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x1,
∴b=﹣2a<0,
∴ab<0,所以结论①正确;
∵抛物线的对称轴为直线x=1,抛物线与x轴的一个交点坐标在(0,0)与(﹣1,0)之间,
∴抛物线与x轴的另一个交点坐标在(2,0)与(3,0)之间,
∴一元二次方程ax2+bx+c=0的正实数根在2和3之间,所以结论②正确;
把B(0,﹣2),A(﹣1,m)代入抛物线得c=﹣2,a﹣b+c=m,
而b=﹣2a,
∴a+2a﹣2=m,
∴,所以结论③正确;
∵点P1(t,y1),P2(t+1,y2)在抛物线上,
∴当点P1、P2都在直线x=1的右侧时,y1<y2,此时t≥1;
当点P1在直线x=1的左侧,点P2在直线x=1的右侧时,y1<y2,此时0<t<1且t+1﹣1>1﹣t,即t<1,
∴当t时,y1<y2,所以结论④错误.
选:B.
12.解:①连接BD,如图1所示:
∵四边形ABCD为菱形,∠A=60°,
∴AB=BC=CD=DA,∠A=∠C=60°,
∴△ABC和△BCD均为等边三角形,
∴AD=BD,∠ADB=∠ADE+∠EDB=60°,∠DBC=60°,
∴∠A=∠DBC=60°,
∵∠EDF=∠A=60°,
∴∠EDB+∠BDF=60°,
∴∠ADE=∠BDF,
在△ADE和△BDF中,
,
∴△ADE≌△BDF(ASA),
∴AE=BF,DE=DF,
结论①正确;
②∵∠EDF=∠A=60°,DE=DF,
∴△DEF为等边三角形,
∴∠DEF=60°,
∴∠AED+∠BEF=120°,
∵∠A=60°,
∴∠AED+∠ADE=120°,
∴∠ADE=∠BEF,
结论②正确;
③由②可知:△DEF为等边三角形,
结论③正确;
④∵△DEF为等边三角形,
∴EF=DE,
∵AE=BF,
∴△BEF的周长=BE+BF+EF=BE+AE+EF=AB+DE,
∵点E在AB边上的位置不同,DE的长也不同,即DE的长随点E位置的变化而变化,
∴△BEF的周长=AB+DE也随点E位置的变化而变化,
即△BEF的周长与点E的位置有关,
结论④不正确,
综上所述:正确的结论是①②③.
选:C.
二.填空题(共6小题,满分24分,每小题4分)
13.解:原式
,
故答案为:.
14.解:设该多项式的另一个因式是x+n.
得(x+2)(x+n)=x2+(n+2)x+2n,
∴n+2=﹣2,
解得n=﹣4,
∴m=2n=2×(﹣4)=﹣8,
故答案为:﹣8.
15.解:∵六边形ABCDEF是正六边形,
∴∠AFE=∠BAF120°,
∵∠EFG=20°,
∴∠AFG=120°﹣20°=100°,
∵AH∥FG,
∴∠FAH=180°﹣100°=80°,
∴∠BAI=120°﹣80°=40°,
∵BI⊥AH,
∴∠ABI=90°﹣40°=50°,
故答案为:50°.
16.解:
=1.
故答案为:1.
17.解:作AD⊥x轴于点D,
∵直线y=x与反比例函数的图象交于点A,
∴设A(m,m),则AD=OD=m,k=m2,
∴OA,
∵OA=OB,
∴OB,
∵S△ABO6,
∴,
∴m2=6,
∴k=6,
故答案为:6.
18.解:作HP⊥BC于点P,则∠FPH=∠BPH=90°,
∵四边形ABCD是矩形,AB=4,BC=6,
∴∠A=∠B=∠C=90°,AD∥BC,
∴四边形ABPH是矩形,
∴PH=AB=4,AH=BP,
由折叠得∠EHJ=∠EHA∠AHF,∠GHK=∠GHD∠DHF,
∴∠EHG=∠EHJ+∠GHK(∠AHF+∠DHF)180°=90°,
同理∠FEH=∠GFE=90°,
∴四边形EFGH是矩形,
∴EH=GF,
∵∠EHJ=∠EHA∠AHF,∠GFK=∠GFC∠CFH,且∠AHF=∠CFH,
∴∠EHA=∠GFC,
在△EHA和△GFC中,
,
∴△EHA≌△GFC(AAS),
∴AH=CF,
∴BP=CF,
∵JH=AH=CF,JF=BF,
∴FH=JH+JF=CF+BF=BC=6,
∴PF2,
∴BP+CF=2AH=6﹣2,
∴AH=3,
故答案为:3.
三.解答题(共7小题,满分78分)
19.解:(1)原式
=2+1﹣1
=2;
(2)原式
=a﹣2.
20.解:(1)由题意得:m75.
答案为:75;
(2)八年级学生的测试成绩更好,理由如下:
因为八年级学生的测试成绩的平均数和中位数均高于七年级,所以八年级学生的测试成绩更好;
(3)400600×(1﹣5%﹣35%﹣30%)=100+180=280(人),
答:估计这两个年级本次测试成绩不低于80分的学生人数大约为280人.
21.解:(1)把x=0代入y=﹣2x+4得:
y=4,
∴点B的坐标为(0,4),
把y=0代入y=﹣2x+4得:
﹣2x+4=0,
解得:x=2,
∴点A的坐标为(2,0),
∵C为AB的中点,
∴点C的坐标为(1,2),
把(1,2)代入得:
k=1×2=2.
(2)过点E作EF⊥x轴于点F,过点D作DG⊥x轴于点G,如图所示:
∵将OC向右平移至PD,点C的坐标为(1,2),
∴DG=2,
∵PE:ED=1:3,
∴,
∵DG⊥x轴,EF⊥x轴,
∴EF∥DG,
∴△PEF∽△PDG,
∴,
∴,
∴E点的纵坐标为,
把代入得:
,
解得:x=4,
∴点E的坐标为.
22.解:设B型汽车的进价为每辆x万元,则A型汽车的进价为每辆1.5x万元,
依题意得10,
解得:x=20,
经检验,x=20是方程的解,1.5x=1.5×20=30,
答:A型汽车的进价为每辆30万元,B型汽车的进价为每辆20万元.
23.解:(1)DM=EM,DM⊥EM,理由如下:
如图,延长EM交AD于点K,
∵EF∥CG∥AD,
∴∠MAK=∠MFE,∠MKA=∠MEF,
∵M是AF的中点,
∴AM=FM,
∴△AMK≌△FME(AAS),
∴AK=EF=EC,KM=EM,
∵AD=CD,
∴AD﹣AK=CD﹣CE,即DK=DE,
∵∠KDE=90°,
∴△KDE是等腰直角三角形,
而KM=EM,
∴DM=EM,DM⊥EM.
(2)(1)中结论仍然成立,理由如下:
如图,延长EM,DA交于点T,
∵EF∥CG∥AD,
∴∠MAT=∠MFE,∠MTA=∠MEF,
∵M是AF的中点,
∴AM=FM,
∴△AMT≌△FME(AAS),
∴AT=EF=EC,TM=EM,
∵AD=CD,
∴AD+AT=CD+CE,即DT=DE,
∵∠TDE=90°,
∴△TDE是等腰直角三角形,
而TM=EM,
∴DM=EM,DM⊥EM.
(3)连接DE,过点M作MR⊥DE于点R,延长EM至H,使MH=ME,连接AH,DH,
当F在DC右侧时,如图,
∵MH=ME,∠AMH=∠EMF,AM=FM,
∴△AMH≌△FME(SAS),
∴AH=EF=EC,∠MAH=∠MFE,
∴AH∥DF,
∴∠DAH+∠ADE=180°,
∴∠DAH+∠CDE=90°,
∴∠DCE+∠CDE=90°,
∴∠DAH=∠DCE,
∵DA=DC,
∴△DAH≌△DCE(SAS),
∴DH=DE,∠ADH=∠CDE,
∴∠HDE=∠ADC=90°,
∵ME=MH,
∴DH⊥EH,DM=MH=EM,
在Rt△CDE中,DE,
∵DM=ME,DM⊥ME,MR⊥DE,
∴MRDE=6=DR=RE,
∴FR=EF+RE=11,
在Rt△RMF中,MF;
当F在DC左侧时,如图,
同法可得DE=12,MR=6=DR=RE,
∴FR=ER﹣FE=6﹣5=1,
在Rt△RMF中,MF,
综上,MF的长为或.
答:MF的长为或.
24.(1)证明:在△ABE和△CBD中,
∵AB=BC,∠ABE=∠CBD,BE=BD,
∴△ABE≌△CBD(SAS),
∴AE=CD,∠FAB=∠BCD.
∵F是Rt△ABE斜边AE的中点,
∴AE=2BF,
∴CD=2BF,
∵,
∴∠FAB=∠FBA.
∴∠FBA=∠BCD,
∵∠FBA+∠FBC=90°,
∴∠FBC+∠BCD=90°.
∴BF⊥CD;
(2)①BF⊥CD;
理由如下:延长BF到点G,使FG=BF,连结AG.延长EB到M,使BE=BM,连接AM并延长交CD于点N.
证△AGB≌△BDC(具体证法过程跟②一样).
∴∠ABG=∠BCD,
∵F是AE中点,B是EM中点,
∴BF是△ABM中位线,
∴BF∥AN,
∴∠ABG=∠BAN=∠BCD,
∴∠ABC=∠ANC=90°,
∴AN⊥CD,
∵BF∥AN,
∴BF⊥CD.
答案为:BF⊥CD;
②证明:延长BF到点G,使FG=BF,连结AG.
∵AF=EF,FG=BF,∠AFG=∠EFB,
∴△AGF≌△EBF(SAS),
∴∠FAG=∠FEB,AG=BE.
∴AG∥BE.
∴∠GAB+∠ABE=180°,
∵∠ABC=∠EBD=90°,
∴∠ABE+∠DBC=180°,
∴∠GAB=∠DBC.
∵BE=BD,
∴AG=BD.
在△AGB和△BDC中,
∵AG=BD,∠GAB=∠DBC,AB=CB,
∴△AGB≌△BDC(SAS),
∴CD=BG.
∵BG=2BF,
∴CD=2BF,
25.解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣x2+3x+4;
(2)令y=﹣x2+3x+4,则x=﹣1或4,
则点B(4,0),
过点A、P分别作y轴的平行线交BC于点N、H,
由点B、C的坐标得,直线BC的表达式为:y=﹣x+4,
当x=﹣1时,y=﹣x+4=5,即点N(﹣1,5),则AN=5,
设点P(x,﹣x2+3x+4),则点H(x,﹣x+4),
则PH=(﹣x2+3x+4)﹣(﹣x+4)=﹣x2+4x,
∵AN∥y轴∥PH,
则△AQN∽△PQH,
∴(x2﹣4x)(x﹣2)2,
即的最大值为;
(3)设E(t,0),当点E在点B的左侧时,若t<3,如图,
过点E作y轴的平行线交CM于点H,过点N作x轴的平行线交EH于点T,
∵∠HEM+∠HME=90°,∠HEM+∠NET=90°,
∴∠HEM=∠ENT,
∵∠EHM=∠NTE=90°,EM=EN,
∴△EHM≌△NTE(AAS),
∴HM=ET=3﹣t,HE=4=TN,
则点N(t+4,t﹣3),
将点N的坐标代入抛物线表达式得:t﹣3=﹣(t+4)2+3(t+4)+4,
解得:t=﹣3±2,
即点E的坐标为:(﹣3+2,0)或(﹣3﹣2,0);
若t=3时,如图,
当点N与点A重合时,EM=EN,∠MEN=90°,
∴E(3,0);
当点E在点B的右侧时,
同理可得,点N的坐标为:(t﹣4,3﹣t),
将点N的坐标代入抛物线表达式得:3﹣t=﹣(t﹣4)2+3(t﹣4)+4,
解得:t=3(舍去)或t=9,
∴E(9,0);
综上,点E的坐标为:(3+2,0)或(3﹣2,0)或(3,0)或(9,0).
第2页(共22页)
同课章节目录
