5.6 函数y=Asin(ωx φ)的图像 课件(共20张PPT)
文档属性
| 名称 | 5.6 函数y=Asin(ωx φ)的图像 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 686.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-09 23:15:02 | ||
图片预览







文档简介
(共20张PPT)
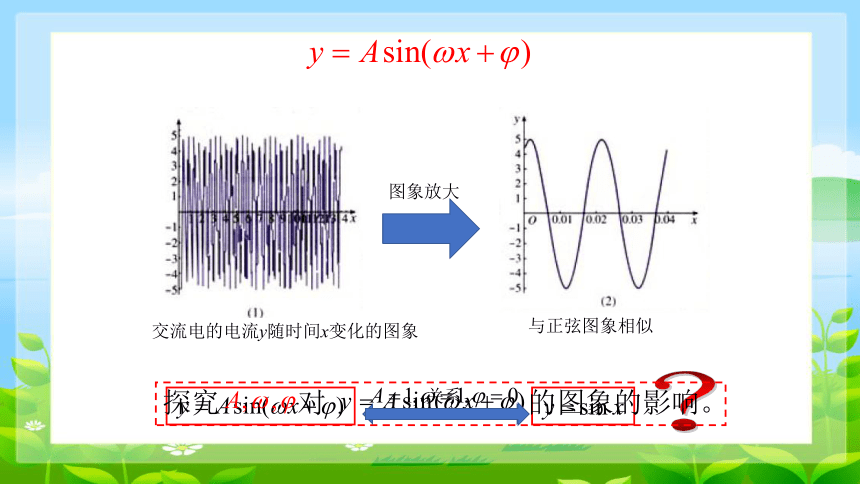
函数 的图象
图象放大
与正弦图象相似
交流电的电流y随时间x变化的图象
关系
探究 对 的图象的影响。
观察 和 的图象关系.
探究 对函数图象的影响
(一)探究 对 的图象的影响
函数 y=sin(x+ )( 0) 的图象可以看作是把y=sinx 的图象上所有的点 (当 >0时)或 (当 <0时)平行移动 个单位而得到的。
所有的点向左( >0)
或向右( <0)平移
| | 个单位
y=sinx
y=sin(x+ )
向左
向右
| |
(左加右减)
观察 和 的图象关系.
(二)探究 对 的图象的影响
函数 y=sin( x+ ) ( >0且 0) 的图象可以看作是把 y=sin (x+ )的图象上所有点的横坐标 (当 >1时)或 (当0< <1时)到原来的 倍(纵坐标不变)而得到的.
伸长
缩短
所有的点横坐标缩短( >1)或伸长(0< <1) 1/ 倍
y=sin(x+ )
y=sin( x+ )
纵坐标不变
探究 对函数图象的影响
(三)探究 对 的图象的影响
观察 和 的图象关系.
函数 y=Asin( x+ ) (A>0且A 1) 的图象可以看作是把y=sin( x+ )的图象上所有点的纵坐标 (当A>1时)或 (当0< A<1时)到原来的 倍(横坐标不变)而得到的.
伸长
缩短
A
y=sin( x+ )
y=Asin( x+ )
所有的点纵坐标伸长(A>1)或缩短(0< A<1) A倍
横坐标不变
y=Asin( x+ ) ,x R的值域是[-A, A],最大值是A,最小值是-A.
探究 对函数图象的影响
思考:函数 的图象经过怎样的变换得到函数的图象?
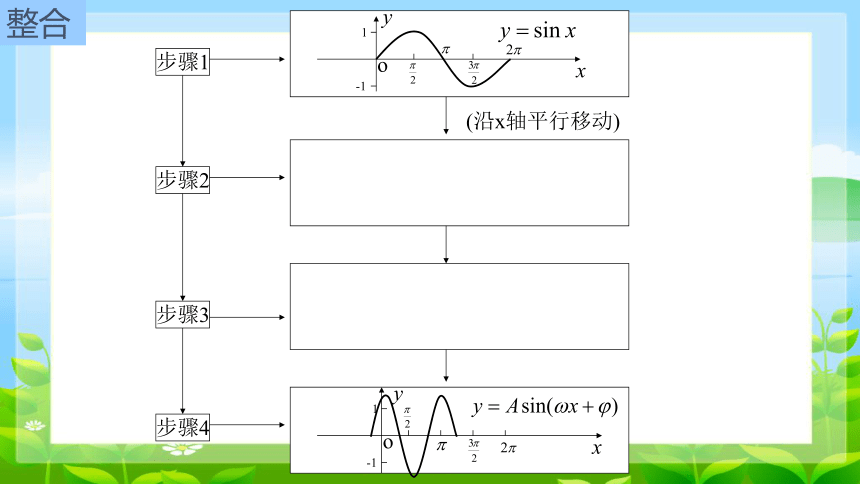
整合
的图象
的图象
的图象
(2)所有的点横坐标缩短 倍
纵坐标不变
(3)所有的点纵坐标伸长3倍
横坐标不变
问题:怎样由 的图象得到
的图象?
整合
步骤1
步骤2
步骤3
步骤4
x
y
o
-1
1
x
y
o
-1
1
(沿x轴平行移动)
整合
问题:怎样由 的图象得到
的图象?
整合
还有别的变换方法吗
函数________
函数
函数________
问题:怎样由 的图象得到
的图象?
整合
*
1、把函数 的图象向右平移 个单位长
度,可得到函数( )的图象。
A、
B、
C、
D、
C
2、为了得到函数 的图象,只要把
函数 的图象上所有的点( )
A、横坐标伸长到原来的4倍,纵坐标不变;
B、横坐标缩短到原来的 倍,纵坐标不变;
C、纵坐标伸长到原来的3倍,横坐标不变;
D、纵坐标缩短到原来的 倍,横坐标不变。
B
3、为了得到函数 的图象,只要把
函数 的图象上所有的点( )
A、向右平行移动 个单位长度;
B、向左平行移动 个单位长度;
C、向右平行移动 个单位长度;
D、向左平行移动 个单位长度;
C
4、为了得到函数 的图象,只要把函数
的图象上所有的点( )
A、向右平行移动 个单位长度;
B、向左平行移动 个单位长度
C、向右平行移动 个单位长度
D、向左平行移动 个单位长度
D
5、先将函数 的图象向右平移 个单位
长度后,再将所得的函数图象上所有点的横坐
标伸长到原来的2倍,可得到函数( )的图象。
A、
B、
C、
D、
C
6、为了得到函数 的图象,只要把
函数 的图象上所有的点( )
A、横坐标伸长到原来的 倍,纵坐标不变;
B、横坐标缩短到原来的 倍,纵坐标不变;
C、纵坐标伸长到原来的 倍,横坐标不变;
D、纵坐标缩短到原来的 倍,横坐标不变。
D
7、先将函数 的图象向右平移 个单位长
度后,再将所得的函数图象上所有点的横坐标
伸长到原来的2倍,最后将所得的函数图象上所
有点的纵坐标伸长到原来的2倍,可得到函数
( )的图象。
A、 B、
C、 D、
A
活动收获
1、知识的收获。
2、数学思想方法的收获。
3、你还有那些困惑吗?
谈谈这节课的收获和遗憾
课后探究
函数 的图象,除了用变换的方法作图外,还可用什么方法作图呢?
课后作业
教材P57:习题第1,2题。
函数 的图象
图象放大
与正弦图象相似
交流电的电流y随时间x变化的图象
关系
探究 对 的图象的影响。
观察 和 的图象关系.
探究 对函数图象的影响
(一)探究 对 的图象的影响
函数 y=sin(x+ )( 0) 的图象可以看作是把y=sinx 的图象上所有的点 (当 >0时)或 (当 <0时)平行移动 个单位而得到的。
所有的点向左( >0)
或向右( <0)平移
| | 个单位
y=sinx
y=sin(x+ )
向左
向右
| |
(左加右减)
观察 和 的图象关系.
(二)探究 对 的图象的影响
函数 y=sin( x+ ) ( >0且 0) 的图象可以看作是把 y=sin (x+ )的图象上所有点的横坐标 (当 >1时)或 (当0< <1时)到原来的 倍(纵坐标不变)而得到的.
伸长
缩短
所有的点横坐标缩短( >1)或伸长(0< <1) 1/ 倍
y=sin(x+ )
y=sin( x+ )
纵坐标不变
探究 对函数图象的影响
(三)探究 对 的图象的影响
观察 和 的图象关系.
函数 y=Asin( x+ ) (A>0且A 1) 的图象可以看作是把y=sin( x+ )的图象上所有点的纵坐标 (当A>1时)或 (当0< A<1时)到原来的 倍(横坐标不变)而得到的.
伸长
缩短
A
y=sin( x+ )
y=Asin( x+ )
所有的点纵坐标伸长(A>1)或缩短(0< A<1) A倍
横坐标不变
y=Asin( x+ ) ,x R的值域是[-A, A],最大值是A,最小值是-A.
探究 对函数图象的影响
思考:函数 的图象经过怎样的变换得到函数的图象?
整合
的图象
的图象
的图象
(2)所有的点横坐标缩短 倍
纵坐标不变
(3)所有的点纵坐标伸长3倍
横坐标不变
问题:怎样由 的图象得到
的图象?
整合
步骤1
步骤2
步骤3
步骤4
x
y
o
-1
1
x
y
o
-1
1
(沿x轴平行移动)
整合
问题:怎样由 的图象得到
的图象?
整合
还有别的变换方法吗
函数________
函数
函数________
问题:怎样由 的图象得到
的图象?
整合
*
1、把函数 的图象向右平移 个单位长
度,可得到函数( )的图象。
A、
B、
C、
D、
C
2、为了得到函数 的图象,只要把
函数 的图象上所有的点( )
A、横坐标伸长到原来的4倍,纵坐标不变;
B、横坐标缩短到原来的 倍,纵坐标不变;
C、纵坐标伸长到原来的3倍,横坐标不变;
D、纵坐标缩短到原来的 倍,横坐标不变。
B
3、为了得到函数 的图象,只要把
函数 的图象上所有的点( )
A、向右平行移动 个单位长度;
B、向左平行移动 个单位长度;
C、向右平行移动 个单位长度;
D、向左平行移动 个单位长度;
C
4、为了得到函数 的图象,只要把函数
的图象上所有的点( )
A、向右平行移动 个单位长度;
B、向左平行移动 个单位长度
C、向右平行移动 个单位长度
D、向左平行移动 个单位长度
D
5、先将函数 的图象向右平移 个单位
长度后,再将所得的函数图象上所有点的横坐
标伸长到原来的2倍,可得到函数( )的图象。
A、
B、
C、
D、
C
6、为了得到函数 的图象,只要把
函数 的图象上所有的点( )
A、横坐标伸长到原来的 倍,纵坐标不变;
B、横坐标缩短到原来的 倍,纵坐标不变;
C、纵坐标伸长到原来的 倍,横坐标不变;
D、纵坐标缩短到原来的 倍,横坐标不变。
D
7、先将函数 的图象向右平移 个单位长
度后,再将所得的函数图象上所有点的横坐标
伸长到原来的2倍,最后将所得的函数图象上所
有点的纵坐标伸长到原来的2倍,可得到函数
( )的图象。
A、 B、
C、 D、
A
活动收获
1、知识的收获。
2、数学思想方法的收获。
3、你还有那些困惑吗?
谈谈这节课的收获和遗憾
课后探究
函数 的图象,除了用变换的方法作图外,还可用什么方法作图呢?
课后作业
教材P57:习题第1,2题。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
