人教版七年级数学下册 9.2 坐标方法的简单应用 同步练习(含详解)
文档属性
| 名称 | 人教版七年级数学下册 9.2 坐标方法的简单应用 同步练习(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-10 13:34:16 | ||
图片预览



文档简介
9.2 坐标方法的简单应用
一、单选题
1.在平面直角坐标系中,将点先向右平移3个单位长度,再向上平移2个单位长度,最后所得点的坐标是( )
A. B. C. D.
2.平移后得到,点对应的点是,则点对应的点、点对应的点的坐标分别是( ).
A. B. C. D.
3.如图,在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点,,则“宝藏”所在地点C的坐标为( )
A. B. C. D.
4.如图,已知点,,将线段平移至的位置,其中点,则点的坐标为( )
A. B. C. D.
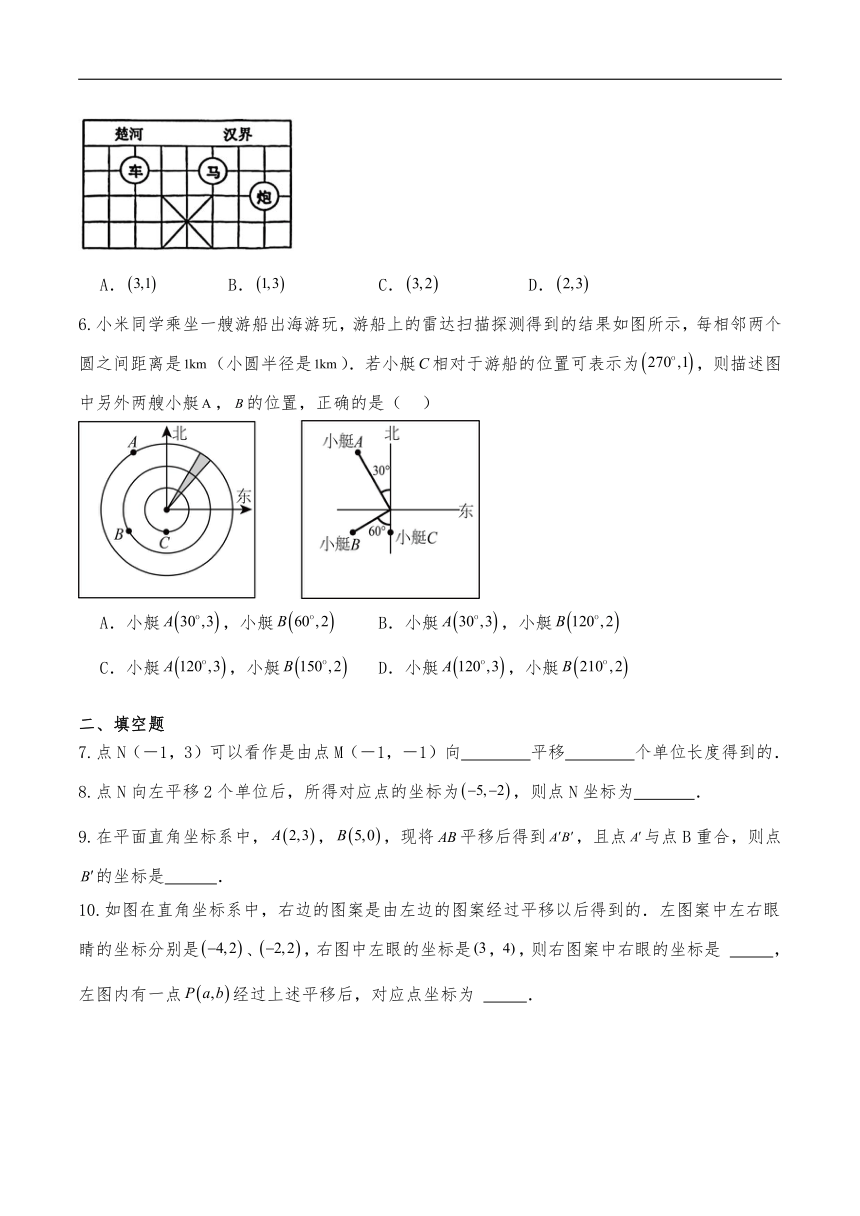
5.如图,是中国象棋棋盘的一部分,已知“车”所在位置的坐标为,“马”所在位置的坐标为,则“炮”所在位置的坐标为( )
A. B. C. D.
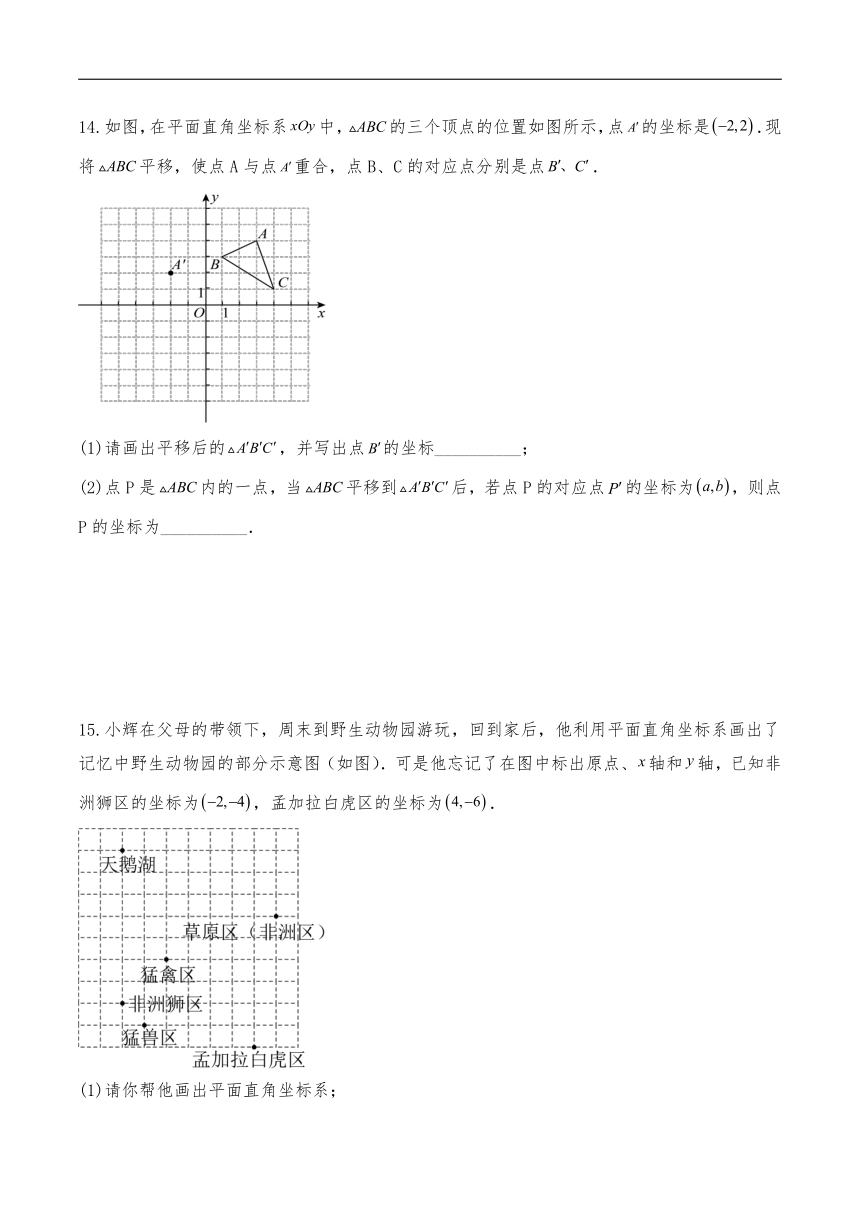
6.小米同学乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是(小圆半径是).若小艇相对于游船的位置可表示为,则描述图中另外两艘小艇,的位置,正确的是( )
A.小艇,小艇 B.小艇,小艇
C.小艇,小艇 D.小艇,小艇
二、填空题
7.点N(-1,3)可以看作是由点M(-1,-1)向 平移 个单位长度得到的.
8.点N向左平移2个单位后,所得对应点的坐标为,则点N坐标为 .
9.在平面直角坐标系中,,,现将平移后得到,且点与点B重合,则点的坐标是 .
10.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是、,右图中左眼的坐标是,,则右图案中右眼的坐标是 ,左图内有一点经过上述平移后,对应点坐标为 .
11.在平面直角坐标系中,线段的两个端点坐标分别为,平移线段,平移后其中一个端点的坐标为,则另一端点的坐标为 .
12.如图,在平面直角坐标系中,线段是由线段平移得到的,小颖不小心将墨汁滴到点B的坐标上,已知A,C,D三点的坐标分别为,则点B的坐标为 .
三、解答题
13.如图是某学校的平面示意图,在8×8的正方形网格中,如果校门所在位置的坐标为,教学楼所在位置的坐标为
(1)请画出符合题意的平面直角坐标系;
(2)在(1)的平面直角坐标系内表示下列位置的坐标:
旗杆_____________;体育馆_____________;
图书馆___________;实验楼_____________.
14.如图,在平面直角坐标系中,的三个顶点的位置如图所示,点的坐标是.现将平移,使点A与点重合,点B、C的对应点分别是点.
(1)请画出平移后的,并写出点的坐标__________;
(2)点P是内的一点,当平移到后,若点P的对应点的坐标为,则点P的坐标为__________.
15.小辉在父母的带领下,周末到野生动物园游玩,回到家后,他利用平面直角坐标系画出了记忆中野生动物园的部分示意图(如图).可是他忘记了在图中标出原点、轴和轴,已知非洲狮区的坐标为,孟加拉白虎区的坐标为.
(1)请你帮他画出平面直角坐标系;
(2)写出天鹅湖与猛禽区的坐标;
(3)若展览馆的坐标为,请在图中标出展览馆的位置.
16.根据右图提供的信息回答问题.
(1)书店在小军家( )方向( )米处.
(2)学校在小军家正北方向800米处,记作“米”,则少年宫在小军家正南方向大约( )米处,记作( )米.
(3)花店在学校南偏东方向400米处,请在右图中标示出来.
17.如图,,,,将向右平移3个单位长度,然后再向上平移1个单位长度,可以得到.
(1)的顶点的坐标为__________;顶点的坐标为_________;顶点的坐标为___________.
(2)在图中画出平移后的.
(3)求的面积.
18.如图,平面直角坐标系中,已知点,,,是的边上任意一点,经过平移后得到,点的对应点为.
(1)在图中画出.
(2)连接,,,求的面积.
(3)连接,若点在轴上,且三角形的面积为8,请直接写出点的坐标.
19.如图,在平面直角坐标系中,已知,,三点,
(1)将向右平移格,再向下平移格,得到,在方格纸中画出.内有一点,则平移后它的对应点的坐标是______.
(2)求三角形的面积;
(3)在轴上是否存在点,使三角形的面积等于三角形的面积的倍?若存在,求出的坐标;若不存在,请说明理由.
20.如图,平面直角坐标系中,,,,,.
(1)求的面积;
(2)如图,点以每秒个单位的速度向下运动至,与此同时,点从原点出发,以每秒个单位的速度沿轴向右运动至,秒后,、、在同一直线上,求的值;
(3)如图,点在线段上,将点向右平移个单位长度至点,若的面积等于,求点坐标.
答案
一、单选题
1.B
【分析】本题考查坐标与图形变化—平移,根据点的坐标的平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减求解即可.
【详解】解:将点先向右平移3个单位,再向上平移2个单位,最后所得点的坐标是,
故选:B.
2.A
【分析】本题考查了平移的性质,先根据点对应的点是判断出平移的方式,再根据平移的方式求出对应的点、点对应的点的坐标即可.
【详解】解:点向右平移4个单位,向上平移5个单位得到,
则.
故选:A.
3.C
【分析】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.根据题意首先确定原点的位置,进而得出“宝藏”点C的位置.
【详解】解:根据两个标志点,可建立如下所示的坐标系,
由平面直角坐标系知,“宝藏”点C的位置是,
故选:C.
4.A
【分析】本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,本题根据对应点的坐标确定出平移规律是解题的关键.根据点A、C的坐标确定出平移规律,然后根据规律求解点D的坐标即可.
【详解】解:∵的对应点C的坐标为,
∴平移规律为横坐标减3,纵坐标加1,
∵点的对应点为D,
∴D的坐标为.
故选:A.
5.A
【分析】本题考查了坐标确定位置,根据平面直角坐标系中,“车”和“马”的坐标确定“炮”所在的横坐标是3,纵坐标是1,便能写出坐标进行选择.
【详解】解:“炮”所在的横坐标是3,纵坐标是1,
∴“炮”的坐标为,
故选:A.
6.D
【分析】本题考查了坐标确定位置,解题的关键是根据向东为起点,逆时针旋转的角度为横坐标,根据每两个圆环之间距离是1千米,可得答案.
【详解】解:图中另外两个小艇、的位置,正确的是小艇,小艇,
故选:D.
二、填空题
7. 上 4
【解析】略
8.
【解析】略
9.
【分析】本题主要考查了平移的性质,解题的关键是熟练掌握坐标平移的特点,右加左减,上加下减.根据平移的性质进行解答即可.
【详解】解:将平移后得到,且点与点重合,
将向右平移3个单位,向下平移3个单位到,
点的坐标为,
即.
故答案为:
10.
【分析】本题考查了点的平移;根据两眼的距离为2,得出右图案中右眼的横坐标为,即可得出右图案中右眼的坐标;根据左眼的坐标从平移到右图中左眼的坐标是,平移方式为向右平移个单位,向上平移个单位,即可得出点平移后的坐标,即可求解.
【详解】解:∵左图案中左右眼睛的坐标分别是、,
∴两眼间的距离为2,且平行于轴,
∵右图中左眼的坐标是,
∴右图案中右眼的横坐标为.
则右图案中右眼的坐标是.
∵左眼的坐标从平移到右图中左眼的坐标是,平移方式为向右平移个单位,向上平移个单位,
∴左图内有一点经过上述平移后,对应点坐标为
故答案为:,.
11.或
【分析】本题主要考查了坐标与图形的变化-平移,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.没有确定对应点时,注意分类讨论.分两种情况讨论,①平移后的对应点的坐标为;②平移后的对应点的坐标为,根据根据平移规律可得另一端点的坐标.
【详解】解:①平移后得到点的坐标为,
∴向右平移个单位,
∴的对应点坐标为,即;
②平移后得到点的坐标为,
∴向右平移个单位,向下平移个单位,
∴的对应点坐标为,即;
综上,另一端点的坐标为或.
故答案为或.
12.
【分析】先根据点A和对应点C的坐标得到平移的规律为:向右平移2个单位,再向上平移1个单位,同步进行的是,点B向右平移2个单位,再向上平移2个单位得到点D.根据此平移规律推断点B的坐标.
【详解】解:∵线段是由线段平移得到的,
∴点平移的对应点为,点B平移的对应点为,
∵点C是点A向右平移2个单位,再向上平移1个单位得到的,
∴点D也是点B向右平移2个单位,再向上平移1个单位得到的,
∴把点向左平移2个单位,再向下平移1个单位得到点B的坐标,
∴点B的坐标是,
故答案为:.
三、解答题
13.(1)建立平面直角坐标系如图所示;
(2)旗杆、体育馆:、图书馆:、实验楼:.
故答案为:,,,
14.(1)解:∵点的坐标是,点的坐标是,
∴平移方向是先向右平移5个单位长度,再向下平移2个单位长度,
∵点的坐标是,点的坐标是,
∴点的坐标是,点的坐标是,
∴平移后的如图所示:
(2)解:由(1)得:平移方向是先向右平移5个单位长度,再向下平移2个单位长度,
∵点P的对应点的坐标为,
∴点P的坐标为;
15.(1)解:如图所示,建立平面直角坐标系:
(2)解:在(1)的坐标系得,天鹅湖的坐标为,猛禽区的坐标为;
(3)解:展览馆的坐标为,在图中标出展览馆的位置,如图所示:
16.(1)解:书店在小军家南偏西方向800米处.
故答案为:南偏西;800;
(2)解:学校在小军家正北方向800米处,记作“米”.则少年宫在小军家正南方向大约1200米处,记作米.
故答案为:1200;;
(3)解:如图,
.
17.(1)解:点的坐标为,顶点的坐标为,顶点的坐标为,
故答案为:,,;
(2)解:
(3)解:.
18.(1)解:∵平移后对应点为,
∴,,;
如图,为所作;
(2)解:的面积
,
,
;
(3)解:设,
,,
,
∵三角形的面积为8,
∴,
解得或,
∴点的坐标为或.
19.(1)解:将向右平移格,是在横轴上平移;再向下平移格,是在纵轴上平移,
∴图像平移后如下图示,
∴是所求图形,
根据平移的规律,内有一点,平移后它的对应点的坐标是,
故答案为:.
(2)解:如图所示,
,,,,
∴,即,
∴三角形的面积为.
(3)解:如图所示,在轴上取一点,已知,,,
∴,点到的距离为,则,
由(2)可知,
∴,
∴,
当时,,即点的坐标为;
当时,,即点的坐标为;
综上所述,存在点,使三角形的面积等于三角形的面积的倍,且点的坐标为或.
20.(1),,,
,,
,,
,
,,,
,,
;
(2)由题意知:,,
,
,
.
(3)连接,,
设,
,
,
,
点向右平移个单位长度得到点,
,
,
,
,
,
一、单选题
1.在平面直角坐标系中,将点先向右平移3个单位长度,再向上平移2个单位长度,最后所得点的坐标是( )
A. B. C. D.
2.平移后得到,点对应的点是,则点对应的点、点对应的点的坐标分别是( ).
A. B. C. D.
3.如图,在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点,,则“宝藏”所在地点C的坐标为( )
A. B. C. D.
4.如图,已知点,,将线段平移至的位置,其中点,则点的坐标为( )
A. B. C. D.
5.如图,是中国象棋棋盘的一部分,已知“车”所在位置的坐标为,“马”所在位置的坐标为,则“炮”所在位置的坐标为( )
A. B. C. D.
6.小米同学乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是(小圆半径是).若小艇相对于游船的位置可表示为,则描述图中另外两艘小艇,的位置,正确的是( )
A.小艇,小艇 B.小艇,小艇
C.小艇,小艇 D.小艇,小艇
二、填空题
7.点N(-1,3)可以看作是由点M(-1,-1)向 平移 个单位长度得到的.
8.点N向左平移2个单位后,所得对应点的坐标为,则点N坐标为 .
9.在平面直角坐标系中,,,现将平移后得到,且点与点B重合,则点的坐标是 .
10.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是、,右图中左眼的坐标是,,则右图案中右眼的坐标是 ,左图内有一点经过上述平移后,对应点坐标为 .
11.在平面直角坐标系中,线段的两个端点坐标分别为,平移线段,平移后其中一个端点的坐标为,则另一端点的坐标为 .
12.如图,在平面直角坐标系中,线段是由线段平移得到的,小颖不小心将墨汁滴到点B的坐标上,已知A,C,D三点的坐标分别为,则点B的坐标为 .
三、解答题
13.如图是某学校的平面示意图,在8×8的正方形网格中,如果校门所在位置的坐标为,教学楼所在位置的坐标为
(1)请画出符合题意的平面直角坐标系;
(2)在(1)的平面直角坐标系内表示下列位置的坐标:
旗杆_____________;体育馆_____________;
图书馆___________;实验楼_____________.
14.如图,在平面直角坐标系中,的三个顶点的位置如图所示,点的坐标是.现将平移,使点A与点重合,点B、C的对应点分别是点.
(1)请画出平移后的,并写出点的坐标__________;
(2)点P是内的一点,当平移到后,若点P的对应点的坐标为,则点P的坐标为__________.
15.小辉在父母的带领下,周末到野生动物园游玩,回到家后,他利用平面直角坐标系画出了记忆中野生动物园的部分示意图(如图).可是他忘记了在图中标出原点、轴和轴,已知非洲狮区的坐标为,孟加拉白虎区的坐标为.
(1)请你帮他画出平面直角坐标系;
(2)写出天鹅湖与猛禽区的坐标;
(3)若展览馆的坐标为,请在图中标出展览馆的位置.
16.根据右图提供的信息回答问题.
(1)书店在小军家( )方向( )米处.
(2)学校在小军家正北方向800米处,记作“米”,则少年宫在小军家正南方向大约( )米处,记作( )米.
(3)花店在学校南偏东方向400米处,请在右图中标示出来.
17.如图,,,,将向右平移3个单位长度,然后再向上平移1个单位长度,可以得到.
(1)的顶点的坐标为__________;顶点的坐标为_________;顶点的坐标为___________.
(2)在图中画出平移后的.
(3)求的面积.
18.如图,平面直角坐标系中,已知点,,,是的边上任意一点,经过平移后得到,点的对应点为.
(1)在图中画出.
(2)连接,,,求的面积.
(3)连接,若点在轴上,且三角形的面积为8,请直接写出点的坐标.
19.如图,在平面直角坐标系中,已知,,三点,
(1)将向右平移格,再向下平移格,得到,在方格纸中画出.内有一点,则平移后它的对应点的坐标是______.
(2)求三角形的面积;
(3)在轴上是否存在点,使三角形的面积等于三角形的面积的倍?若存在,求出的坐标;若不存在,请说明理由.
20.如图,平面直角坐标系中,,,,,.
(1)求的面积;
(2)如图,点以每秒个单位的速度向下运动至,与此同时,点从原点出发,以每秒个单位的速度沿轴向右运动至,秒后,、、在同一直线上,求的值;
(3)如图,点在线段上,将点向右平移个单位长度至点,若的面积等于,求点坐标.
答案
一、单选题
1.B
【分析】本题考查坐标与图形变化—平移,根据点的坐标的平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减求解即可.
【详解】解:将点先向右平移3个单位,再向上平移2个单位,最后所得点的坐标是,
故选:B.
2.A
【分析】本题考查了平移的性质,先根据点对应的点是判断出平移的方式,再根据平移的方式求出对应的点、点对应的点的坐标即可.
【详解】解:点向右平移4个单位,向上平移5个单位得到,
则.
故选:A.
3.C
【分析】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.根据题意首先确定原点的位置,进而得出“宝藏”点C的位置.
【详解】解:根据两个标志点,可建立如下所示的坐标系,
由平面直角坐标系知,“宝藏”点C的位置是,
故选:C.
4.A
【分析】本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,本题根据对应点的坐标确定出平移规律是解题的关键.根据点A、C的坐标确定出平移规律,然后根据规律求解点D的坐标即可.
【详解】解:∵的对应点C的坐标为,
∴平移规律为横坐标减3,纵坐标加1,
∵点的对应点为D,
∴D的坐标为.
故选:A.
5.A
【分析】本题考查了坐标确定位置,根据平面直角坐标系中,“车”和“马”的坐标确定“炮”所在的横坐标是3,纵坐标是1,便能写出坐标进行选择.
【详解】解:“炮”所在的横坐标是3,纵坐标是1,
∴“炮”的坐标为,
故选:A.
6.D
【分析】本题考查了坐标确定位置,解题的关键是根据向东为起点,逆时针旋转的角度为横坐标,根据每两个圆环之间距离是1千米,可得答案.
【详解】解:图中另外两个小艇、的位置,正确的是小艇,小艇,
故选:D.
二、填空题
7. 上 4
【解析】略
8.
【解析】略
9.
【分析】本题主要考查了平移的性质,解题的关键是熟练掌握坐标平移的特点,右加左减,上加下减.根据平移的性质进行解答即可.
【详解】解:将平移后得到,且点与点重合,
将向右平移3个单位,向下平移3个单位到,
点的坐标为,
即.
故答案为:
10.
【分析】本题考查了点的平移;根据两眼的距离为2,得出右图案中右眼的横坐标为,即可得出右图案中右眼的坐标;根据左眼的坐标从平移到右图中左眼的坐标是,平移方式为向右平移个单位,向上平移个单位,即可得出点平移后的坐标,即可求解.
【详解】解:∵左图案中左右眼睛的坐标分别是、,
∴两眼间的距离为2,且平行于轴,
∵右图中左眼的坐标是,
∴右图案中右眼的横坐标为.
则右图案中右眼的坐标是.
∵左眼的坐标从平移到右图中左眼的坐标是,平移方式为向右平移个单位,向上平移个单位,
∴左图内有一点经过上述平移后,对应点坐标为
故答案为:,.
11.或
【分析】本题主要考查了坐标与图形的变化-平移,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.没有确定对应点时,注意分类讨论.分两种情况讨论,①平移后的对应点的坐标为;②平移后的对应点的坐标为,根据根据平移规律可得另一端点的坐标.
【详解】解:①平移后得到点的坐标为,
∴向右平移个单位,
∴的对应点坐标为,即;
②平移后得到点的坐标为,
∴向右平移个单位,向下平移个单位,
∴的对应点坐标为,即;
综上,另一端点的坐标为或.
故答案为或.
12.
【分析】先根据点A和对应点C的坐标得到平移的规律为:向右平移2个单位,再向上平移1个单位,同步进行的是,点B向右平移2个单位,再向上平移2个单位得到点D.根据此平移规律推断点B的坐标.
【详解】解:∵线段是由线段平移得到的,
∴点平移的对应点为,点B平移的对应点为,
∵点C是点A向右平移2个单位,再向上平移1个单位得到的,
∴点D也是点B向右平移2个单位,再向上平移1个单位得到的,
∴把点向左平移2个单位,再向下平移1个单位得到点B的坐标,
∴点B的坐标是,
故答案为:.
三、解答题
13.(1)建立平面直角坐标系如图所示;
(2)旗杆、体育馆:、图书馆:、实验楼:.
故答案为:,,,
14.(1)解:∵点的坐标是,点的坐标是,
∴平移方向是先向右平移5个单位长度,再向下平移2个单位长度,
∵点的坐标是,点的坐标是,
∴点的坐标是,点的坐标是,
∴平移后的如图所示:
(2)解:由(1)得:平移方向是先向右平移5个单位长度,再向下平移2个单位长度,
∵点P的对应点的坐标为,
∴点P的坐标为;
15.(1)解:如图所示,建立平面直角坐标系:
(2)解:在(1)的坐标系得,天鹅湖的坐标为,猛禽区的坐标为;
(3)解:展览馆的坐标为,在图中标出展览馆的位置,如图所示:
16.(1)解:书店在小军家南偏西方向800米处.
故答案为:南偏西;800;
(2)解:学校在小军家正北方向800米处,记作“米”.则少年宫在小军家正南方向大约1200米处,记作米.
故答案为:1200;;
(3)解:如图,
.
17.(1)解:点的坐标为,顶点的坐标为,顶点的坐标为,
故答案为:,,;
(2)解:
(3)解:.
18.(1)解:∵平移后对应点为,
∴,,;
如图,为所作;
(2)解:的面积
,
,
;
(3)解:设,
,,
,
∵三角形的面积为8,
∴,
解得或,
∴点的坐标为或.
19.(1)解:将向右平移格,是在横轴上平移;再向下平移格,是在纵轴上平移,
∴图像平移后如下图示,
∴是所求图形,
根据平移的规律,内有一点,平移后它的对应点的坐标是,
故答案为:.
(2)解:如图所示,
,,,,
∴,即,
∴三角形的面积为.
(3)解:如图所示,在轴上取一点,已知,,,
∴,点到的距离为,则,
由(2)可知,
∴,
∴,
当时,,即点的坐标为;
当时,,即点的坐标为;
综上所述,存在点,使三角形的面积等于三角形的面积的倍,且点的坐标为或.
20.(1),,,
,,
,,
,
,,,
,,
;
(2)由题意知:,,
,
,
.
(3)连接,,
设,
,
,
,
点向右平移个单位长度得到点,
,
,
,
,
,
同课章节目录
