2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练(含答案)
文档属性
| 名称 | 2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 953.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练
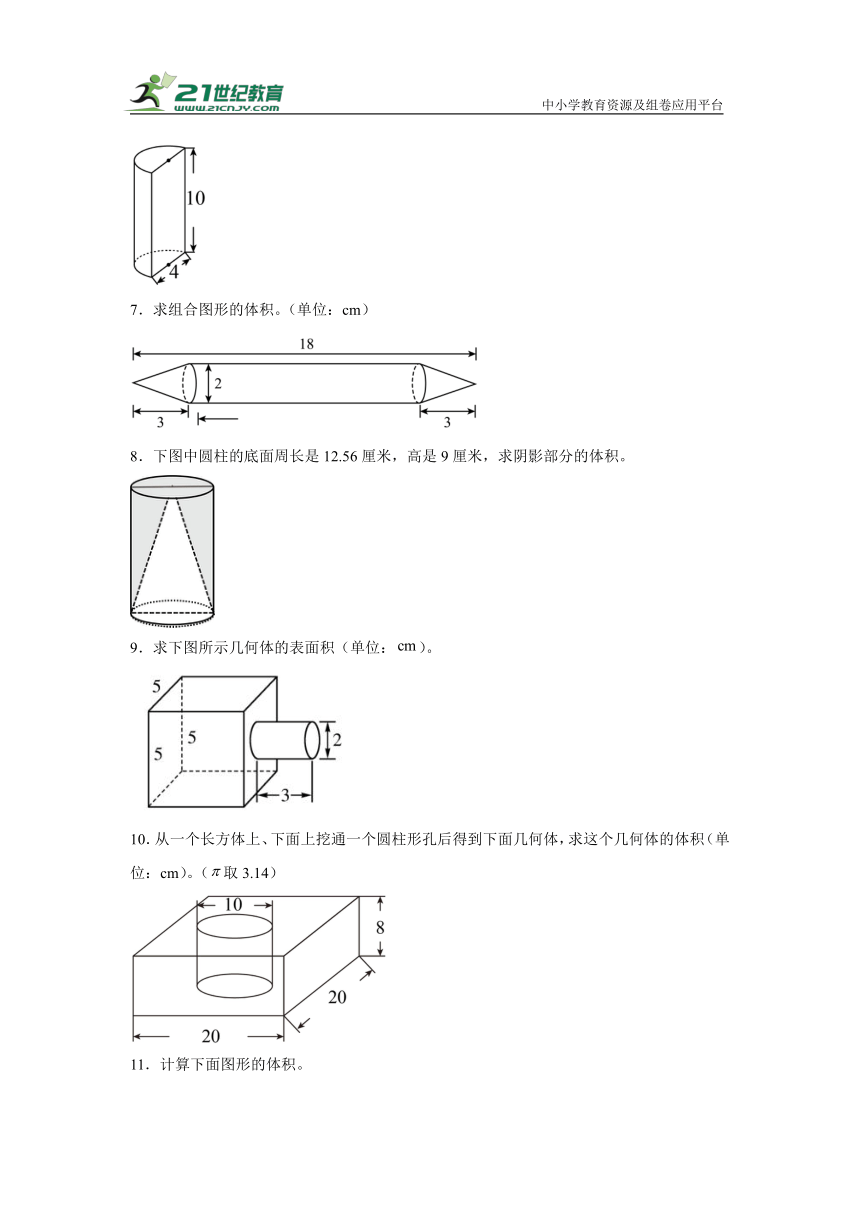
1.计算如图图形的体积。
2.计算下面物体的体积。
3.求如图的体积。(π取3.14)
4.求图形的体积(单位:厘米)(π取3.14)。
5.求下面图形的体积。(单位:厘米)
6.下面是一个圆柱沿着底面直径竖直对半切开后的图形,求它的表面积。(单位:cm)
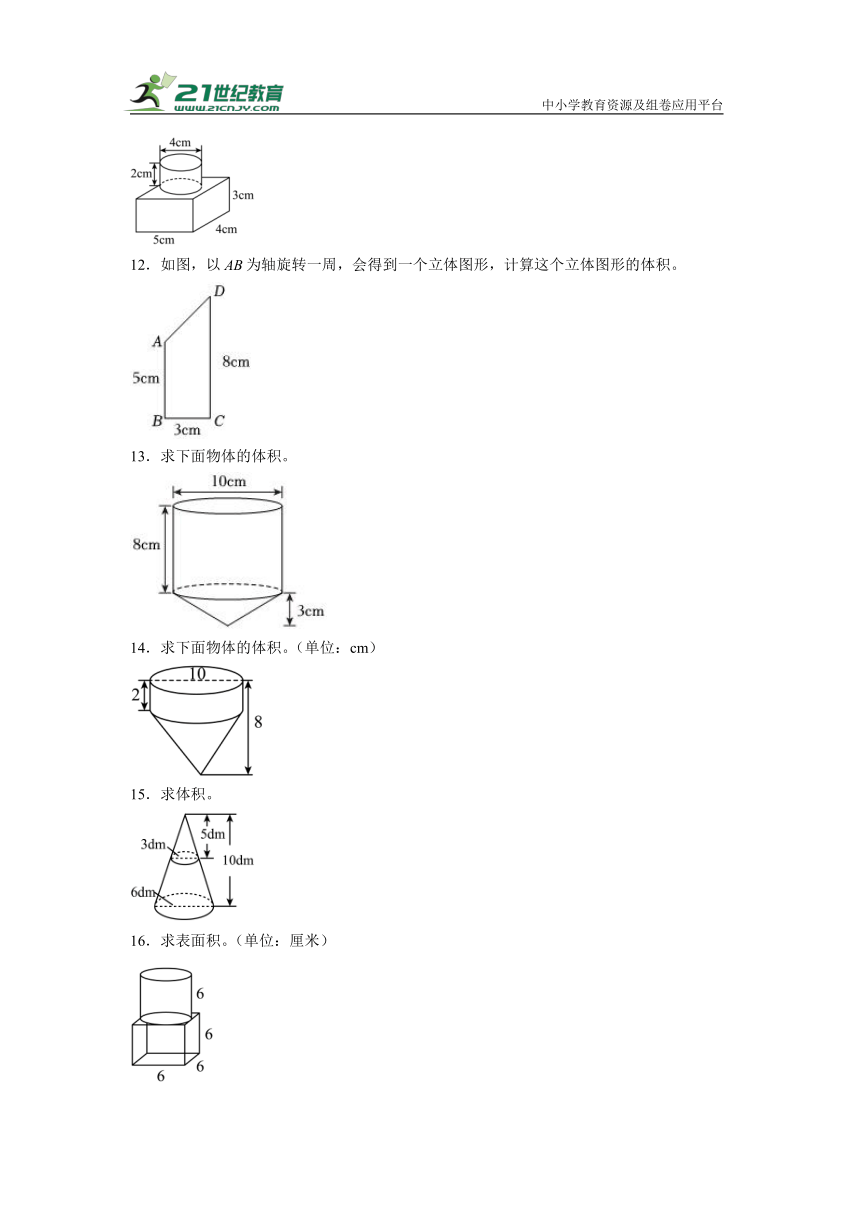
7.求组合图形的体积。(单位:cm)
8.下图中圆柱的底面周长是12.56厘米,高是9厘米,求阴影部分的体积。
9.求下图所示几何体的表面积(单位:)。
10.从一个长方体上、下面上挖通一个圆柱形孔后得到下面几何体,求这个几何体的体积(单位:cm)。(取3.14)
11.计算下面图形的体积。
12.如图,以为轴旋转一周,会得到一个立体图形,计算这个立体图形的体积。
13.求下面物体的体积。
14.求下面物体的体积。(单位:cm)
15.求体积。
16.求表面积。(单位:厘米)
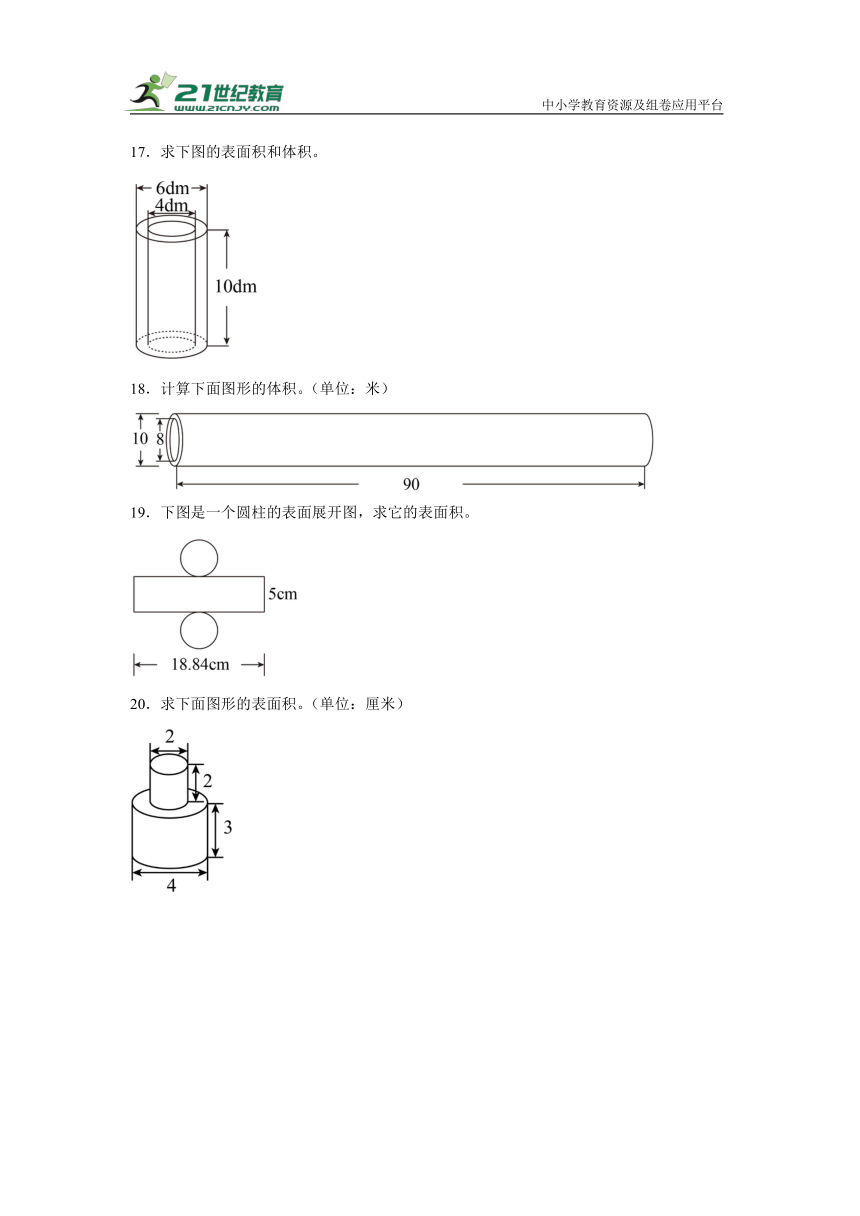
17.求下图的表面积和体积。
18.计算下面图形的体积。(单位:米)
19.下图是一个圆柱的表面展开图,求它的表面积。
20.求下面图形的表面积。(单位:厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练》参考答案
1.15.7cm3
【详解】根据圆柱的体积公式:V=πr2h和圆锥的体积公式:V=πr2h,代入公式计算。
【解答】3.14×(2÷2)2×4+×3.14×(2÷2)2×3
=3.14×12×4+×3.14×12×3
=3.14×1×4+×3.14×1×3
=12.56+3.14
=15.7(cm3)
图形的体积是15.7cm3。
2.565.2dm3;791.28cm3
【分析】(1)根据圆锥的体积公式V=πr2h,代入数据计算,求出圆锥的体积;
(2)观察图形是一个空心的圆柱,底面是圆环,那么它的体积V=S环h=π(R2-r2)h,代入数据计算,求出空心圆柱的体积。
【详解】(1)×3.14×(12÷2)2×15
=×3.14×62×15
=×3.14×36×15
=565.2(dm3)
圆锥的体积是565.2dm3。
(2)3.14×[(10÷2)2-(4÷2)2 ]×12
=3.14×[52-22 ]×12
=3.14×[25-4]×12
=3.14×21×12
=791.28(cm3)
圆柱的体积是791.28cm3。
3.125.6
【分析】2个完全一样的原图立体图形可以拼成一个高为(12+8)、底面直径是4的圆柱体,所以此图的体积是拼成的圆柱体积的一半;利用圆柱体的体积公式计算出体积即可。
【详解】
它的体积是125.6。
4.214.2立方厘米
【分析】观察图形可知,图形的体积=圆柱的体积×+长方体的体积,根据圆柱的体积公式V=πr2h,长方体的体积公式V=abh,代入数据计算即可求解。
【详解】3.14×22×10×+6×10×2
=3.14×4×10×+60×2
=94.2+120
=214.2(立方厘米)
图形的体积是214.2立方厘米。
5.66180立方厘米
【分析】由图可知,该图形的体积可由一个长70厘米,宽30厘米,高36厘米的长方体体积减去一个底面直径为20厘米,高为30厘米的圆柱体体积。根据及圆柱的体积公式代入数据解答。
【详解】
(立方厘米)
(立方厘米)
(立方厘米)
6.115.36cm2
【分析】这个图形的表面积=圆柱一个底面积+圆柱侧面积的一半+一个长方形的面积,根据圆的面积,圆柱侧面积,求出这个图形的表面积即可。
【详解】表面积:
(cm2)
图形的表面积是115.36cm2。
7.43.96cm3
【分析】观察图形可知,该组合图形的体积=中间圆柱的体积+两边的两个圆锥的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,据此代入数值进行计算即可。
【详解】3.14×(2÷2)2×(18-3×2)+×3.14×(2÷2)2×3×2
=3.14×12×(18-6)+×3.14×12×3×2
=3.14×12×12+×3.14×12×3×2
=3.14×1×12+×3.14×1×3×2
=37.68+6.28
=43.96(cm3)
8.75.36立方厘米
【分析】已知圆柱的底面周长是12.56厘米,根据圆柱的底面周长C=2πr可知,r=C÷π÷2,由此求出圆柱的底面半径;
观察图形可知,阴影部分的体积=圆柱的体积-圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】圆柱的底面半径:
12.56÷3.14÷2
=4÷2
=2(厘米)
阴影部分的体积:
3.14×22×9-×3.14×22×9
=3.14×4×9-×3.14×4×9
=113.04-37.68
=75.36(立方厘米)
答:阴影部分的体积是75.36立方厘米。
9.168.84
【分析】观察图形可知,图形的表面积等于正方体表面积与圆柱侧面积之和,再根据正方体的表面积=棱长×棱长×6,圆柱侧面积=底面周长×高,进行解答即可。
【详解】正方体表面积:
(cm2)
圆柱侧面积:
(cm2)
几何体表面积:
10.2572立方厘米
【分析】求这个几何体的体积,用长方体的体积-圆柱的体积,长方体的体积=长×宽×高,圆柱的体积=底面积×高,据此列式解答。
【详解】10÷2=5(厘米)
20×20×8-3.14××8
=400×8-3.14×200
=3200-628
=2572(立方厘米)
11.85.12cm3
【分析】观察图形可知,图形的体积=圆柱的体积+长方体的体积,根据圆柱的体积V=πr2h,长方体的体积V=abh,代入数据计算求解。
【详解】圆柱的体积:
3.14×(4÷2)2×2
=3.14×22×2
=3.14×4×2
=25.12(cm3)
长方体的体积:
5×4×3
=20×3
=60(cm3)
一共:25.12+60=85.12(cm3)
图形的体积是85.12cm3。
12.197.82
【分析】由题意可知,以AB为轴旋转一周会得到一个上面镂空为圆锥的圆柱,用圆柱的体积减去圆锥的体积即可,据此解答。
【详解】
=3.14×9×8-×3.14×9×3
=226.08-28.26
=197.82()
13.706.5cm3
【分析】根据题意可知,底面半径是(10÷2)cm,根据圆柱的体积公式:V=πr2h和圆锥的体积公式:V=πr2h,分别代入数据求出圆柱和圆锥的体积,再相加即可。
【详解】
(cm3)
这个立体图形的体积是706.5cm3。
14.314立方厘米
【分析】这个几何体是由上面一个圆柱和下面的一个圆锥组成,分别将圆柱和圆锥的体积算出来,再相加即可算出总体积。其中底面是一个圆形,底面积=π×半径2,圆柱的体积=底面积×高,圆锥的体积=底面积×高×,其中要注意圆锥的高是由总高减去圆柱的高得到,最后根据公式计算体积即可。
【详解】半径:10÷2=5(厘米) 圆锥的高:8-2=6(厘米)
圆柱体积:
圆锥体积:
总体积:
15.82.425
【分析】圆台的体积等于大圆锥的体积减去小圆锥的体积,根据圆锥的体积,代入数据即=82.425(),据此解答。
【详解】由分析可知:
=
=3.14×30-3.14×3.75
=94.2-11.775
=82.425()
所以这个圆台的体积是82.425。
【点睛】本题考查圆锥体积公式的运用,学生需熟练掌握。
16.329.04平方厘米
【分析】图形是一个棱长为6厘米的正方体上面放了底面直径和高等于6厘米的一个圆柱体,圆柱体上底面的面积刚好等于圆柱下底面遮盖掉的正方体部分面积,因此整个图形的表面积应该等于正方体的表面积加上圆柱的侧面积。其中正方体的表面积=棱长×棱长×6,圆柱的侧面积等于底面周长乘高也就是等于。
【详解】(平方厘米)
(平方厘米)
表面积:216+113.04=329.04(平方厘米)
图形的表面积是329.04平方厘米。
17.345.4平方分米;157立方分米
【分析】分析图形可知,所求图形的底面是环形,根据圆环的面积公式,求出图形的底面积,所求图形的表面积=大圆柱的侧面积+小圆柱的侧面积+环形底面积×2,根据圆柱的侧面积公式,代入数据即可算出图形的表面积。所求图形的体积=环形底面积×高,据此解答。
【详解】
(平方分米)
(平方分米)
(立方分米)
即图形的表面积是345.4平方分米,体积是157立方分米。
18.2543.4立方米
【分析】圆柱体积=底面积×高,据此先分别求出大圆柱和小圆柱的体积,再相减即可得出题中图形的体积。
【详解】3.14×(10÷2)2×90-3.14×(8÷2)2×90
=3.14×52×90-3.14×42×90
=7065-4521.6
=2543.4(立方米)
所以,这个图形的体积是2543.4立方米。
19.150.72平方厘米
【分析】观察图形可知,圆柱的底面周长是18.84厘米,圆柱的高是5厘米;根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出底面半径;再根据圆柱的表面积公式:表面积=底面积×2+侧面积,代入数据,即可解答。
【详解】18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32×2+18.84×5
=3.14×9×2+94.2
=28.26×2+94.2
=56.52+94.2
=150.72(平方厘米)
它的表面积是150.72平方厘米。
20.62.8平方厘米
【分析】如图所示,整个图形的表面积=小圆柱体的侧面积+大圆柱体的表面积(注意扣除下底面的面积),据此解答。
【详解】小圆柱体的侧面积:
(平方厘米)
大圆柱体的表面积:
(平方厘米)
整个图形的表面积:(平方厘米)
答案第2页,共9页
答案第9页,共9页
中小学教育资源及组卷应用平台
2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练
1.计算如图图形的体积。
2.计算下面物体的体积。
3.求如图的体积。(π取3.14)
4.求图形的体积(单位:厘米)(π取3.14)。
5.求下面图形的体积。(单位:厘米)
6.下面是一个圆柱沿着底面直径竖直对半切开后的图形,求它的表面积。(单位:cm)
7.求组合图形的体积。(单位:cm)
8.下图中圆柱的底面周长是12.56厘米,高是9厘米,求阴影部分的体积。
9.求下图所示几何体的表面积(单位:)。
10.从一个长方体上、下面上挖通一个圆柱形孔后得到下面几何体,求这个几何体的体积(单位:cm)。(取3.14)
11.计算下面图形的体积。
12.如图,以为轴旋转一周,会得到一个立体图形,计算这个立体图形的体积。
13.求下面物体的体积。
14.求下面物体的体积。(单位:cm)
15.求体积。
16.求表面积。(单位:厘米)
17.求下图的表面积和体积。
18.计算下面图形的体积。(单位:米)
19.下图是一个圆柱的表面展开图,求它的表面积。
20.求下面图形的表面积。(单位:厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练》参考答案
1.15.7cm3
【详解】根据圆柱的体积公式:V=πr2h和圆锥的体积公式:V=πr2h,代入公式计算。
【解答】3.14×(2÷2)2×4+×3.14×(2÷2)2×3
=3.14×12×4+×3.14×12×3
=3.14×1×4+×3.14×1×3
=12.56+3.14
=15.7(cm3)
图形的体积是15.7cm3。
2.565.2dm3;791.28cm3
【分析】(1)根据圆锥的体积公式V=πr2h,代入数据计算,求出圆锥的体积;
(2)观察图形是一个空心的圆柱,底面是圆环,那么它的体积V=S环h=π(R2-r2)h,代入数据计算,求出空心圆柱的体积。
【详解】(1)×3.14×(12÷2)2×15
=×3.14×62×15
=×3.14×36×15
=565.2(dm3)
圆锥的体积是565.2dm3。
(2)3.14×[(10÷2)2-(4÷2)2 ]×12
=3.14×[52-22 ]×12
=3.14×[25-4]×12
=3.14×21×12
=791.28(cm3)
圆柱的体积是791.28cm3。
3.125.6
【分析】2个完全一样的原图立体图形可以拼成一个高为(12+8)、底面直径是4的圆柱体,所以此图的体积是拼成的圆柱体积的一半;利用圆柱体的体积公式计算出体积即可。
【详解】
它的体积是125.6。
4.214.2立方厘米
【分析】观察图形可知,图形的体积=圆柱的体积×+长方体的体积,根据圆柱的体积公式V=πr2h,长方体的体积公式V=abh,代入数据计算即可求解。
【详解】3.14×22×10×+6×10×2
=3.14×4×10×+60×2
=94.2+120
=214.2(立方厘米)
图形的体积是214.2立方厘米。
5.66180立方厘米
【分析】由图可知,该图形的体积可由一个长70厘米,宽30厘米,高36厘米的长方体体积减去一个底面直径为20厘米,高为30厘米的圆柱体体积。根据及圆柱的体积公式代入数据解答。
【详解】
(立方厘米)
(立方厘米)
(立方厘米)
6.115.36cm2
【分析】这个图形的表面积=圆柱一个底面积+圆柱侧面积的一半+一个长方形的面积,根据圆的面积,圆柱侧面积,求出这个图形的表面积即可。
【详解】表面积:
(cm2)
图形的表面积是115.36cm2。
7.43.96cm3
【分析】观察图形可知,该组合图形的体积=中间圆柱的体积+两边的两个圆锥的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,据此代入数值进行计算即可。
【详解】3.14×(2÷2)2×(18-3×2)+×3.14×(2÷2)2×3×2
=3.14×12×(18-6)+×3.14×12×3×2
=3.14×12×12+×3.14×12×3×2
=3.14×1×12+×3.14×1×3×2
=37.68+6.28
=43.96(cm3)
8.75.36立方厘米
【分析】已知圆柱的底面周长是12.56厘米,根据圆柱的底面周长C=2πr可知,r=C÷π÷2,由此求出圆柱的底面半径;
观察图形可知,阴影部分的体积=圆柱的体积-圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算求解。
【详解】圆柱的底面半径:
12.56÷3.14÷2
=4÷2
=2(厘米)
阴影部分的体积:
3.14×22×9-×3.14×22×9
=3.14×4×9-×3.14×4×9
=113.04-37.68
=75.36(立方厘米)
答:阴影部分的体积是75.36立方厘米。
9.168.84
【分析】观察图形可知,图形的表面积等于正方体表面积与圆柱侧面积之和,再根据正方体的表面积=棱长×棱长×6,圆柱侧面积=底面周长×高,进行解答即可。
【详解】正方体表面积:
(cm2)
圆柱侧面积:
(cm2)
几何体表面积:
10.2572立方厘米
【分析】求这个几何体的体积,用长方体的体积-圆柱的体积,长方体的体积=长×宽×高,圆柱的体积=底面积×高,据此列式解答。
【详解】10÷2=5(厘米)
20×20×8-3.14××8
=400×8-3.14×200
=3200-628
=2572(立方厘米)
11.85.12cm3
【分析】观察图形可知,图形的体积=圆柱的体积+长方体的体积,根据圆柱的体积V=πr2h,长方体的体积V=abh,代入数据计算求解。
【详解】圆柱的体积:
3.14×(4÷2)2×2
=3.14×22×2
=3.14×4×2
=25.12(cm3)
长方体的体积:
5×4×3
=20×3
=60(cm3)
一共:25.12+60=85.12(cm3)
图形的体积是85.12cm3。
12.197.82
【分析】由题意可知,以AB为轴旋转一周会得到一个上面镂空为圆锥的圆柱,用圆柱的体积减去圆锥的体积即可,据此解答。
【详解】
=3.14×9×8-×3.14×9×3
=226.08-28.26
=197.82()
13.706.5cm3
【分析】根据题意可知,底面半径是(10÷2)cm,根据圆柱的体积公式:V=πr2h和圆锥的体积公式:V=πr2h,分别代入数据求出圆柱和圆锥的体积,再相加即可。
【详解】
(cm3)
这个立体图形的体积是706.5cm3。
14.314立方厘米
【分析】这个几何体是由上面一个圆柱和下面的一个圆锥组成,分别将圆柱和圆锥的体积算出来,再相加即可算出总体积。其中底面是一个圆形,底面积=π×半径2,圆柱的体积=底面积×高,圆锥的体积=底面积×高×,其中要注意圆锥的高是由总高减去圆柱的高得到,最后根据公式计算体积即可。
【详解】半径:10÷2=5(厘米) 圆锥的高:8-2=6(厘米)
圆柱体积:
圆锥体积:
总体积:
15.82.425
【分析】圆台的体积等于大圆锥的体积减去小圆锥的体积,根据圆锥的体积,代入数据即=82.425(),据此解答。
【详解】由分析可知:
=
=3.14×30-3.14×3.75
=94.2-11.775
=82.425()
所以这个圆台的体积是82.425。
【点睛】本题考查圆锥体积公式的运用,学生需熟练掌握。
16.329.04平方厘米
【分析】图形是一个棱长为6厘米的正方体上面放了底面直径和高等于6厘米的一个圆柱体,圆柱体上底面的面积刚好等于圆柱下底面遮盖掉的正方体部分面积,因此整个图形的表面积应该等于正方体的表面积加上圆柱的侧面积。其中正方体的表面积=棱长×棱长×6,圆柱的侧面积等于底面周长乘高也就是等于。
【详解】(平方厘米)
(平方厘米)
表面积:216+113.04=329.04(平方厘米)
图形的表面积是329.04平方厘米。
17.345.4平方分米;157立方分米
【分析】分析图形可知,所求图形的底面是环形,根据圆环的面积公式,求出图形的底面积,所求图形的表面积=大圆柱的侧面积+小圆柱的侧面积+环形底面积×2,根据圆柱的侧面积公式,代入数据即可算出图形的表面积。所求图形的体积=环形底面积×高,据此解答。
【详解】
(平方分米)
(平方分米)
(立方分米)
即图形的表面积是345.4平方分米,体积是157立方分米。
18.2543.4立方米
【分析】圆柱体积=底面积×高,据此先分别求出大圆柱和小圆柱的体积,再相减即可得出题中图形的体积。
【详解】3.14×(10÷2)2×90-3.14×(8÷2)2×90
=3.14×52×90-3.14×42×90
=7065-4521.6
=2543.4(立方米)
所以,这个图形的体积是2543.4立方米。
19.150.72平方厘米
【分析】观察图形可知,圆柱的底面周长是18.84厘米,圆柱的高是5厘米;根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出底面半径;再根据圆柱的表面积公式:表面积=底面积×2+侧面积,代入数据,即可解答。
【详解】18.84÷3.14÷2
=6÷2
=3(厘米)
3.14×32×2+18.84×5
=3.14×9×2+94.2
=28.26×2+94.2
=56.52+94.2
=150.72(平方厘米)
它的表面积是150.72平方厘米。
20.62.8平方厘米
【分析】如图所示,整个图形的表面积=小圆柱体的侧面积+大圆柱体的表面积(注意扣除下底面的面积),据此解答。
【详解】小圆柱体的侧面积:
(平方厘米)
大圆柱体的表面积:
(平方厘米)
整个图形的表面积:(平方厘米)
答案第2页,共9页
答案第9页,共9页
