人教版八年级数学下册 19.3 课题学习选择方案 课时训练(含答案)
文档属性
| 名称 | 人教版八年级数学下册 19.3 课题学习选择方案 课时训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-11 10:00:10 | ||
图片预览




文档简介
八年级数学下册人教版第十九章第3节《课题学习 选择方案》
课时训练
一、单选题
1.已知某租车公司有A,B两种租车方案:A方案为先支付500元,再按每千米元收费;B方案直接按每千米1元收费,已知小明租车花费了800元,若他使用的是最优租车方案,则他的行驶里程是( )
A.600千米 B.700千米 C.800千米 D.900千米
2.网红“脏脏包”是时下最流行的一款面包,“脏脏包”正如其名,它看起来脏脏的,吃完以后嘴巴和手上会因沾上巧克力而变“脏”,因而得名“脏脏包”.某面包店每天固定制作甲、乙两种款型的脏脏包共200个,且所有脏脏包当天全部售出,原料成本、销售单价及店员生产提成如表所示:
甲(元/个) 乙(元/个)
原料成本 12 8
销售单价 18 12
生产提成 1 0.6
设该店每天制作甲款型的脏脏包x(个),每天获得的总利润为y(元).则y与x之间的函数关系式为( )
A.y=1.6x+680 B.y=﹣1.6x+680
C.y=﹣1.6x﹣680 D.y=﹣1.6x﹣6800
3.如图表示的是某公司一种产品30天的销售情况,其中图①是该产品日销售量y(件)与日期t(日)的函数图象,图②是该产品单件的销售利润w(元)与日期:t(日)的函数图象.下列结论错误的是( )
A.第25天的销售量为200件 B.第6天销售一件产品的利润是19元
C.第20天和第30天的日销售利润相等 D.第18天的日销售利润高于第25天的日销售利润
4.如图,在平面直角坐标系中的位置如图所示,,点,的坐标分别为,,将沿轴向左平移,当点落在直线上时,平移的距离为( )
A.8 B.9 C.10 D.11
5.某电脑公司经营A,B两种台式电脑,分析过去的销售记录可以知道:每台A型电脑可盈利200元,每台B型电脑可盈利300元;在同一时期内,A型电脑的销售量不小于B型电脑销售量的4倍.已知该公司在同一时期内销售这两种电脑共210台,则该公司在这一时期内销售这两种电脑能获得的最大利润是( )
A.42000元 B.46200元 C.52500元 D.63000元
6.哥弟俩同时从家去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进,弟弟步行每分钟,哥哥骑自行车每分钟行驶,如图是两人之间的距离,与弟弟步行时间之间的函数图象,已知弟弟从家出发时离上课时间还有分钟,当他行至快到学校时,发现可能要迟到,于是弟弟加快了步伐,以米每分钟的速度前进,结果到上课时恰好到校,下列错误的是( )
A.点表示哥哥已经到达学校
B.哥哥与弟弟相距的最大距离是米
C.他们家与学校之间的距离为米
D.的函数表达式为
7.甲,乙两车从地开往地,并以各自的速度匀速行驶,甲车比乙车早出发,并且甲车途中休息了,甲、乙两车行驶的路程与甲车的行驶时间的函数关系如图所示.当甲、乙两车相距时,乙车的行驶时间为( )
A.或 B.或 C. D.
8.如图,把放在平面直角坐标系中,其中,,A,B的坐标分别为.将沿x轴向右平移,当点C落在直线上时,线段扫过所形成图形的面积为( )
A.16 B.20 C.28 D.
9.小李计划通过社会实践活动赚钱买一本标价为43元的书,他以1.1元/千克的价格从批发市场购进若干数量的西瓜去销售,在销售了之后,余下的打七五折全部售完,若销售金额(元)与售出西瓜的数量之间的关系如图所示,则下列结论正确的是( )
A.降价后西瓜的单价为2元/千克
B.小李一共进了西瓜
C.小李这次社会实践活动赚的钱可以买到43元的书
D.降价前的单价比降价后的单价多0.6元
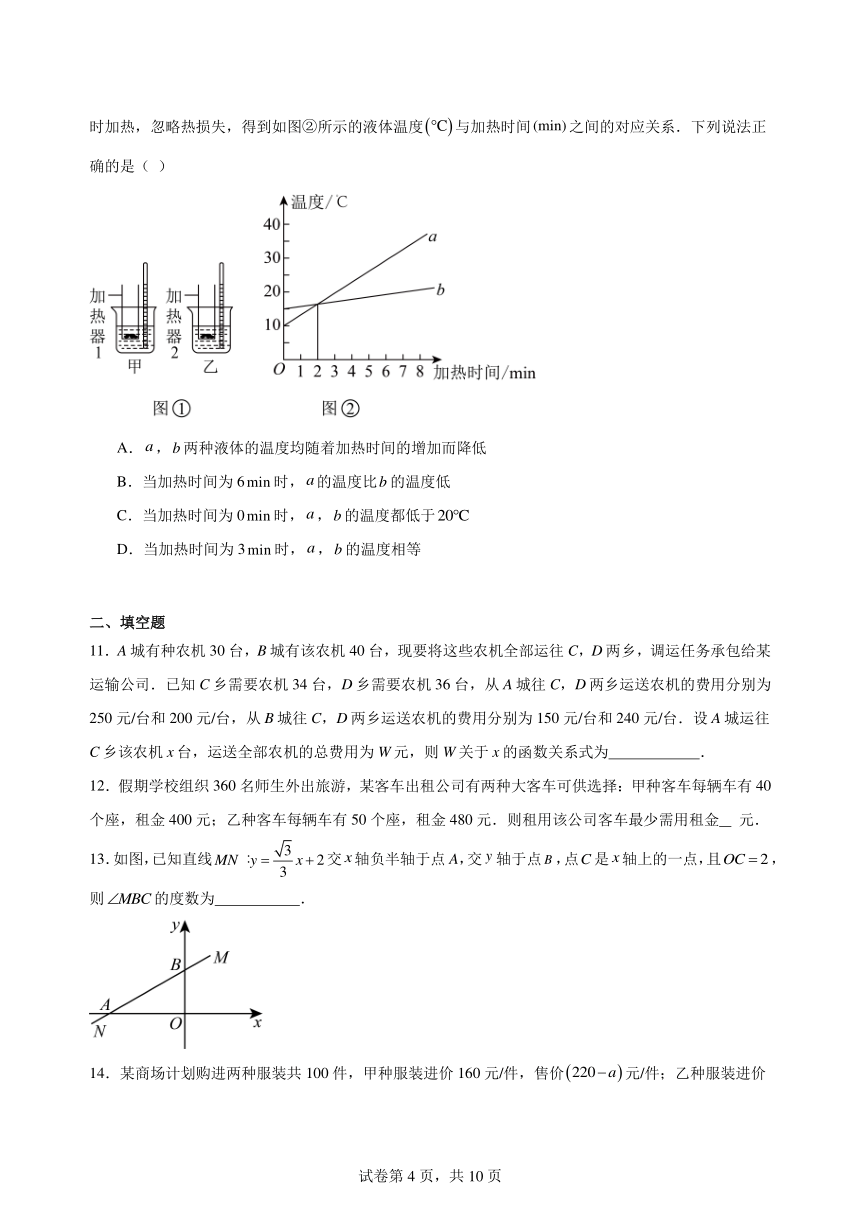
10.如图①所示,甲、乙两个相同容器中分别装有相同体积的,两种液体,现用相同的电加热器同时加热,忽略热损失,得到如图②所示的液体温度与加热时间之间的对应关系.下列说法正确的是( )
A.,两种液体的温度均随着加热时间的增加而降低
B.当加热时间为6时,的温度比的温度低
C.当加热时间为0时,,的温度都低于
D.当加热时间为3时,,的温度相等
二、填空题
11.A城有种农机30台,B城有该农机40台,现要将这些农机全部运往C,D两乡,调运任务承包给某运输公司.已知C乡需要农机34台,D乡需要农机36台,从A城往C,D两乡运送农机的费用分别为250元/台和200元/台,从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.设A城运往C乡该农机x台,运送全部农机的总费用为W元,则W关于x的函数关系式为 .
12.假期学校组织360名师生外出旅游,某客车出租公司有两种大客车可供选择:甲种客车每辆车有40个座,租金400元;乙种客车每辆车有50个座,租金480元.则租用该公司客车最少需用租金 元.
13.如图,已知直线交轴负半轴于点A,交轴于点,点是轴上的一点,且,则的度数为 .
14.某商场计划购进两种服装共100件,甲种服装进价160元/件,售价元/件;乙种服装进价元/件,售价160元/件.设购进甲种服装件,两种服装全部售完,商场获利最大利润为4950元,则的值为 .(其中)
15.某公司新产品上市天全部售完,图①表示产品的市场日销售量与上市时间之间的关系,图②表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是 元;已知当时,单件产品的销售利润w与t之间的函数关系式为,则第天的日销售利润为 元.
16.货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发后休息,直至与货车相遇后,以原速度继续行驶,设两车出发时间为x(单位:h),货车、轿车与甲地的距离为(单位:),(单位:),图中的线段、折线分别表示,与x之间的函数关系.则以下结论中,所有正确结论的序号为
①轿车行驶的速度为;
②货车行驶的速度为;
③线段所在直线的函数表达式为;
④两车出发2小时或4小时后相距.
17.甲、乙两人在一条直线道路上分别从A,两地同时骑摩托车出发,相向而行.当两人相遇后,甲继续向地前进甲到达地时停止运动,乙也立即调头返回地.在整个运动过程中,甲、乙均保持各自的速度匀速行驶.若甲、乙两人之间的距离米与乙运动的时间秒之间的关系如图所示,则A,两地之间的距离为 米.
18.如图,一次函数的图象与轴、轴分别交于点和点,点的坐标为,点,分别是线段,上的动点,且,则的长为 ;当的值取最小值时,点的坐标为 .
三、解答题
19.甲、乙两机器人从地出发,沿相同路线前往地(到达后停止运动),图中,分别表示甲、乙两机器人前往目的地所走的路程,,(单位:)随甲出发的时间(单位:)变化的函数图象.
(1),两地的距离为_______;
(2)求关于的函数解析式;
(3)求乙机器人出发多长时间后追上甲,并求出此时机器人距离地的距离.
20.某校校长暑假带领该校的“星级学生”去研学旅行,甲、乙两家旅行社的服务质量相同,且全票票价都是元,经过协商,甲旅行社说:“若校长买一张全票,则学生可享受六五折优惠.”乙旅行社说:“包括校长在内都享受七折优惠.”若设星级学生人数为人,甲旅行社收费为元,乙旅行社收费为元.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)若参加研学旅行的学生至人,请就学生人数讨论哪家旅行社更优惠.
21.“阶梯电价”具体收费方法是第一档每户用电不超过240度,每度电价0.6元;第二档用电超过240度,但不超过400度,则超过部分每度提价0.05元;第三档用电超过400度,超过部分每度提高0.3元.
(1)设用电量为x度,求出居民费用表达式;
(2)某居民家10月份交电费222元,求该居民家10月份用电度数.
22.为响应国家关于推动各级各类生产设备、服务设备更新和技术改造的号召,某公司计划将办公电脑全部更新为国产某品牌,市场调研发现,品牌的电脑单价比品牌电脑的单价少元,通过预算得知,用万元购买品牌电脑比购买品牌电脑多台.
(1)试求,两种品牌电脑的单价分别是多少元;
(2)该公司计划购买,两种品牌的电脑一共台,且购买品牌电脑的数量不少于品牌电脑的,试求出该公司费用最少的购买方案.
23.某新能源汽车经销商购进紧凑和中级两种型号的新能源汽车,据了解3辆中级型汽车、2辆紧凑型汽车的进价共计104万元;2辆紧凑型汽车比3辆中级型汽车的进价少40万元.
(1)求中级型和紧凑型汽车两种型号汽车的进货单价;
(2)该店准备购进中级型和紧凑型汽车两种型号的新能源汽车100辆,已知中级型汽车的售价为27万元/辆,紧凑型汽车的售价为20万元/辆.根据销售经验,购中级型汽车的数量不低于25辆,设购进辆中级型汽车,100辆车全部售完获利万元,该经销商应购进中级型和紧凑型汽车各多少辆.才能使最大?最大为多少万元?
24.在落实“精准扶贫”战略中,三峡库区驻村干部组织村民依托电商平台组建了土特产专卖店,专门将从本地各家各户进货的甲、乙两种商品销售到全国各地.2021年3月份,该专卖店购进甲、乙两种商品,每个乙种商品的价格比每个甲种商品的价格2倍少20元,用900元购进甲种商品的数量与用1200元购进乙种商品的数量相同.
(1)求每个甲、乙两种商品的进价分别是多少元?
(2)若专卖店购进甲、乙两种商品共100个,且甲种商品的数量不多于乙种商品的数量,设购进甲m个,总成本是y元,求y与m的函数关系式,并求出最少成本的方案和最少成本.
25.在平面直角坐标系中,直线与轴交于点,与轴交于点,直线交于点.
(1)求点、、的坐标;
(2)在平面直角坐标系中有一点,求的面积与的函数关系式;
(3)为直线上的动点,过点作轴的平行线,交直线于点,点在轴上,是否存在点,使为等腰直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
26.小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米.小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁.图中折线和线段分别表示两人离学校的路程(千米)与所经过的时间(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在天一阁查阅资料的时间为________分钟,小聪返回学校的速度为________千米/分钟;
(2)请你求出小明离开学校的路程(千米)与所经过的时间(分钟)之间的函数关系式;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
27.如图,在平面直角坐标系中,点,分别在轴,轴上,线段,的长是方程组的解,点是直线与直线的交点,点在线段上,.
(1)求点的坐标;
(2)求直线的解析式;
(3)是直线上的点,在平面内是否存在点,使以,,,为顶点的四边形是菱形(邻边相等的平行四边形)?若存在,请写出点的坐标;若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1-10 CACDB DBBCC
11.
12.3520
13.或
14.9
15.
16.①③
17.
18.
19.(1)解:由图象可知,A,B两地的距离为m,
故答案为:;
(2)解:设关于x的函数解析式为,
将,代入得,,
解得,,
∴;
(3)解:设关于x的函数解析式为,
将代入得,,
解得,,
∴;
令,
解得,,
∴(),
∴乙机器人出发后追上甲;
∵(),
∴此时它们与A地的距离为;
20.(1)解:根据题意得:,
,
,;
(2)解:①当时,,
解得:,
当学生人数是人时,两家旅行社的收费是一样的;
②当时,,
解得:;
当(为整数)时,乙旅行社更优惠;
③当时,,
解得:,
当(为整数)时,甲旅行社更优惠.
21.(1)解:设用电量为度,居民费用为,
则根据题意,分三种情况:
当用电量时,
则;
当用电量时,
则
;
当用电量时,
则
;
综上,居民费用表达式为:;
(2)解:设该居民家月份用电量为度,
,
该居民家月份用电量位于第二档,即:,
根据题意可得:,
解得:,
该居民家月份用电度数为度.
22.(1)解:设品牌电脑的单价是万元,则品牌电脑的单价是万元,根据题意得:,
化简得
解得:,(舍去),
经检验,是所列方程的解,且符合题意,
∴品牌电脑的单价是万元元,则品牌电脑的单价是万元即元.
答:品牌电脑的单价是元,品牌电脑的单价是元;
(2)解:设购买台品牌电脑,则购买台品牌电脑,
根据题意得:,
解得:.
设学校购买这些电脑需要元,则,
即,
,
随的增大而减小,
当时,取得最小值,最小值为(元).此时,
∴该公司费用最少的购买方案为购买台电脑,购买台电脑,最少需要元.
23.(1)解:设中级型汽车进货单价为元和紧凑型汽车进货单价为元,
由题意得,,
解得,
答:中级型汽车进货单价为元和紧凑型汽车进货单价为元.
(2)解:由题可得,,
,
,
随的增大而减小,
当时,有最大值为,
该经销商应购进中级型汽车辆,紧凑型汽车辆时,最大为万元.
24.(1)解:设每个甲种商品的进价为x元,
由题意可得:,
解得:,
经检验:是原方程的解,
∴每个甲、乙两种商品的进价分别是30元和40元;
(2)解:∵购进甲m个,则购进乙个,
则,
∴,
则,
∵,
∴当时,y最小,
即成本最少的方案为:购进甲种商品50个,乙种商品50个,最少成本为3500元.
25.(1)解:∵直线与轴交于点,与轴交于点,
当时,;
当时,
∴
∵直线交于点.
∴,
解得,
∴点;
(2)解:由题意得点P在直线上,设直线与直线交于点E,交x轴于点F,
将代入得,
∴,
①当点P在点E下方时,即,如图:
;
当点P在点E上方时,即,如图:
,
综上所述:的面积S与m的函数关系式为:;
(3)解:令直线为,直线为,
,则,
,
①如图1,若,,
过点Q作,
∴点G为中点,
∴,
则有,
,
或,
,或,
②如图2,图3,若或,
则,
,
或,
,或.
综上所述,M的坐标为或或或.
26.(1)解:根据图象可以得到:表示小聪的路程与时间的关系.
表示从学校到宁波天一阁,段表示查阅资料的时间,从第分钟,到分钟,则共用了分钟,
段表示从宁波天一阁到学校,时间是从第分钟到第分钟,共用了分钟,路程是千米,则速度是千米分钟,
(2)表示小明的路程与时间的关系,分钟走了千米,速度是千米分钟,则路程与时间的关系式是:
(3)设的函数关系式是,代入点
解得:
联立
解得:
当小聪与小明迎面相遇时,他们离学校的路程是千米.
27.(1)解:解方程组,得,
,
,
即.
设直线的解析式为,
则,解得,
直线的解析式为.
联立,解得,
点的坐标为.
(2)解:设点的坐标为,
,
,解得.
点在线段上,
,
.
设直线的解析式为,
把代入,
得,
解得,
直线的解析式为.
(3)解:存在.理由如下:
直线的解析式为,
记直线与轴交于点,
.
如图,当四边形为菱形时,,
,
有,
设点的坐标为,
有,
解得,
得点的坐标为;
当四边形为菱形时,,由,
同理可得点的坐标为;
易知直线与轴的交点的坐标为,
,
当四边形为菱形时,点的坐标为;
易知当以,,,为顶点的四边形是以为对角线的菱形时,
由菱形对角线互相垂直平分可得,
点与点关于对称,且,
,
点的坐标为.
综上所述,以,,,为顶点的四边形是菱形时,点的坐标为或或或.
答案第1页,共2页
答案第1页,共2页
课时训练
一、单选题
1.已知某租车公司有A,B两种租车方案:A方案为先支付500元,再按每千米元收费;B方案直接按每千米1元收费,已知小明租车花费了800元,若他使用的是最优租车方案,则他的行驶里程是( )
A.600千米 B.700千米 C.800千米 D.900千米
2.网红“脏脏包”是时下最流行的一款面包,“脏脏包”正如其名,它看起来脏脏的,吃完以后嘴巴和手上会因沾上巧克力而变“脏”,因而得名“脏脏包”.某面包店每天固定制作甲、乙两种款型的脏脏包共200个,且所有脏脏包当天全部售出,原料成本、销售单价及店员生产提成如表所示:
甲(元/个) 乙(元/个)
原料成本 12 8
销售单价 18 12
生产提成 1 0.6
设该店每天制作甲款型的脏脏包x(个),每天获得的总利润为y(元).则y与x之间的函数关系式为( )
A.y=1.6x+680 B.y=﹣1.6x+680
C.y=﹣1.6x﹣680 D.y=﹣1.6x﹣6800
3.如图表示的是某公司一种产品30天的销售情况,其中图①是该产品日销售量y(件)与日期t(日)的函数图象,图②是该产品单件的销售利润w(元)与日期:t(日)的函数图象.下列结论错误的是( )
A.第25天的销售量为200件 B.第6天销售一件产品的利润是19元
C.第20天和第30天的日销售利润相等 D.第18天的日销售利润高于第25天的日销售利润
4.如图,在平面直角坐标系中的位置如图所示,,点,的坐标分别为,,将沿轴向左平移,当点落在直线上时,平移的距离为( )
A.8 B.9 C.10 D.11
5.某电脑公司经营A,B两种台式电脑,分析过去的销售记录可以知道:每台A型电脑可盈利200元,每台B型电脑可盈利300元;在同一时期内,A型电脑的销售量不小于B型电脑销售量的4倍.已知该公司在同一时期内销售这两种电脑共210台,则该公司在这一时期内销售这两种电脑能获得的最大利润是( )
A.42000元 B.46200元 C.52500元 D.63000元
6.哥弟俩同时从家去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进,弟弟步行每分钟,哥哥骑自行车每分钟行驶,如图是两人之间的距离,与弟弟步行时间之间的函数图象,已知弟弟从家出发时离上课时间还有分钟,当他行至快到学校时,发现可能要迟到,于是弟弟加快了步伐,以米每分钟的速度前进,结果到上课时恰好到校,下列错误的是( )
A.点表示哥哥已经到达学校
B.哥哥与弟弟相距的最大距离是米
C.他们家与学校之间的距离为米
D.的函数表达式为
7.甲,乙两车从地开往地,并以各自的速度匀速行驶,甲车比乙车早出发,并且甲车途中休息了,甲、乙两车行驶的路程与甲车的行驶时间的函数关系如图所示.当甲、乙两车相距时,乙车的行驶时间为( )
A.或 B.或 C. D.
8.如图,把放在平面直角坐标系中,其中,,A,B的坐标分别为.将沿x轴向右平移,当点C落在直线上时,线段扫过所形成图形的面积为( )
A.16 B.20 C.28 D.
9.小李计划通过社会实践活动赚钱买一本标价为43元的书,他以1.1元/千克的价格从批发市场购进若干数量的西瓜去销售,在销售了之后,余下的打七五折全部售完,若销售金额(元)与售出西瓜的数量之间的关系如图所示,则下列结论正确的是( )
A.降价后西瓜的单价为2元/千克
B.小李一共进了西瓜
C.小李这次社会实践活动赚的钱可以买到43元的书
D.降价前的单价比降价后的单价多0.6元
10.如图①所示,甲、乙两个相同容器中分别装有相同体积的,两种液体,现用相同的电加热器同时加热,忽略热损失,得到如图②所示的液体温度与加热时间之间的对应关系.下列说法正确的是( )
A.,两种液体的温度均随着加热时间的增加而降低
B.当加热时间为6时,的温度比的温度低
C.当加热时间为0时,,的温度都低于
D.当加热时间为3时,,的温度相等
二、填空题
11.A城有种农机30台,B城有该农机40台,现要将这些农机全部运往C,D两乡,调运任务承包给某运输公司.已知C乡需要农机34台,D乡需要农机36台,从A城往C,D两乡运送农机的费用分别为250元/台和200元/台,从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.设A城运往C乡该农机x台,运送全部农机的总费用为W元,则W关于x的函数关系式为 .
12.假期学校组织360名师生外出旅游,某客车出租公司有两种大客车可供选择:甲种客车每辆车有40个座,租金400元;乙种客车每辆车有50个座,租金480元.则租用该公司客车最少需用租金 元.
13.如图,已知直线交轴负半轴于点A,交轴于点,点是轴上的一点,且,则的度数为 .
14.某商场计划购进两种服装共100件,甲种服装进价160元/件,售价元/件;乙种服装进价元/件,售价160元/件.设购进甲种服装件,两种服装全部售完,商场获利最大利润为4950元,则的值为 .(其中)
15.某公司新产品上市天全部售完,图①表示产品的市场日销售量与上市时间之间的关系,图②表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是 元;已知当时,单件产品的销售利润w与t之间的函数关系式为,则第天的日销售利润为 元.
16.货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发后休息,直至与货车相遇后,以原速度继续行驶,设两车出发时间为x(单位:h),货车、轿车与甲地的距离为(单位:),(单位:),图中的线段、折线分别表示,与x之间的函数关系.则以下结论中,所有正确结论的序号为
①轿车行驶的速度为;
②货车行驶的速度为;
③线段所在直线的函数表达式为;
④两车出发2小时或4小时后相距.
17.甲、乙两人在一条直线道路上分别从A,两地同时骑摩托车出发,相向而行.当两人相遇后,甲继续向地前进甲到达地时停止运动,乙也立即调头返回地.在整个运动过程中,甲、乙均保持各自的速度匀速行驶.若甲、乙两人之间的距离米与乙运动的时间秒之间的关系如图所示,则A,两地之间的距离为 米.
18.如图,一次函数的图象与轴、轴分别交于点和点,点的坐标为,点,分别是线段,上的动点,且,则的长为 ;当的值取最小值时,点的坐标为 .
三、解答题
19.甲、乙两机器人从地出发,沿相同路线前往地(到达后停止运动),图中,分别表示甲、乙两机器人前往目的地所走的路程,,(单位:)随甲出发的时间(单位:)变化的函数图象.
(1),两地的距离为_______;
(2)求关于的函数解析式;
(3)求乙机器人出发多长时间后追上甲,并求出此时机器人距离地的距离.
20.某校校长暑假带领该校的“星级学生”去研学旅行,甲、乙两家旅行社的服务质量相同,且全票票价都是元,经过协商,甲旅行社说:“若校长买一张全票,则学生可享受六五折优惠.”乙旅行社说:“包括校长在内都享受七折优惠.”若设星级学生人数为人,甲旅行社收费为元,乙旅行社收费为元.
(1)分别写出两家旅行社的收费与学生人数的关系式;
(2)若参加研学旅行的学生至人,请就学生人数讨论哪家旅行社更优惠.
21.“阶梯电价”具体收费方法是第一档每户用电不超过240度,每度电价0.6元;第二档用电超过240度,但不超过400度,则超过部分每度提价0.05元;第三档用电超过400度,超过部分每度提高0.3元.
(1)设用电量为x度,求出居民费用表达式;
(2)某居民家10月份交电费222元,求该居民家10月份用电度数.
22.为响应国家关于推动各级各类生产设备、服务设备更新和技术改造的号召,某公司计划将办公电脑全部更新为国产某品牌,市场调研发现,品牌的电脑单价比品牌电脑的单价少元,通过预算得知,用万元购买品牌电脑比购买品牌电脑多台.
(1)试求,两种品牌电脑的单价分别是多少元;
(2)该公司计划购买,两种品牌的电脑一共台,且购买品牌电脑的数量不少于品牌电脑的,试求出该公司费用最少的购买方案.
23.某新能源汽车经销商购进紧凑和中级两种型号的新能源汽车,据了解3辆中级型汽车、2辆紧凑型汽车的进价共计104万元;2辆紧凑型汽车比3辆中级型汽车的进价少40万元.
(1)求中级型和紧凑型汽车两种型号汽车的进货单价;
(2)该店准备购进中级型和紧凑型汽车两种型号的新能源汽车100辆,已知中级型汽车的售价为27万元/辆,紧凑型汽车的售价为20万元/辆.根据销售经验,购中级型汽车的数量不低于25辆,设购进辆中级型汽车,100辆车全部售完获利万元,该经销商应购进中级型和紧凑型汽车各多少辆.才能使最大?最大为多少万元?
24.在落实“精准扶贫”战略中,三峡库区驻村干部组织村民依托电商平台组建了土特产专卖店,专门将从本地各家各户进货的甲、乙两种商品销售到全国各地.2021年3月份,该专卖店购进甲、乙两种商品,每个乙种商品的价格比每个甲种商品的价格2倍少20元,用900元购进甲种商品的数量与用1200元购进乙种商品的数量相同.
(1)求每个甲、乙两种商品的进价分别是多少元?
(2)若专卖店购进甲、乙两种商品共100个,且甲种商品的数量不多于乙种商品的数量,设购进甲m个,总成本是y元,求y与m的函数关系式,并求出最少成本的方案和最少成本.
25.在平面直角坐标系中,直线与轴交于点,与轴交于点,直线交于点.
(1)求点、、的坐标;
(2)在平面直角坐标系中有一点,求的面积与的函数关系式;
(3)为直线上的动点,过点作轴的平行线,交直线于点,点在轴上,是否存在点,使为等腰直角三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
26.小聪和小明沿同一条路同时从学校出发到宁波天一阁查阅资料,学校与天一阁的路程是4千米.小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达天一阁.图中折线和线段分别表示两人离学校的路程(千米)与所经过的时间(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在天一阁查阅资料的时间为________分钟,小聪返回学校的速度为________千米/分钟;
(2)请你求出小明离开学校的路程(千米)与所经过的时间(分钟)之间的函数关系式;
(3)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
27.如图,在平面直角坐标系中,点,分别在轴,轴上,线段,的长是方程组的解,点是直线与直线的交点,点在线段上,.
(1)求点的坐标;
(2)求直线的解析式;
(3)是直线上的点,在平面内是否存在点,使以,,,为顶点的四边形是菱形(邻边相等的平行四边形)?若存在,请写出点的坐标;若不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1-10 CACDB DBBCC
11.
12.3520
13.或
14.9
15.
16.①③
17.
18.
19.(1)解:由图象可知,A,B两地的距离为m,
故答案为:;
(2)解:设关于x的函数解析式为,
将,代入得,,
解得,,
∴;
(3)解:设关于x的函数解析式为,
将代入得,,
解得,,
∴;
令,
解得,,
∴(),
∴乙机器人出发后追上甲;
∵(),
∴此时它们与A地的距离为;
20.(1)解:根据题意得:,
,
,;
(2)解:①当时,,
解得:,
当学生人数是人时,两家旅行社的收费是一样的;
②当时,,
解得:;
当(为整数)时,乙旅行社更优惠;
③当时,,
解得:,
当(为整数)时,甲旅行社更优惠.
21.(1)解:设用电量为度,居民费用为,
则根据题意,分三种情况:
当用电量时,
则;
当用电量时,
则
;
当用电量时,
则
;
综上,居民费用表达式为:;
(2)解:设该居民家月份用电量为度,
,
该居民家月份用电量位于第二档,即:,
根据题意可得:,
解得:,
该居民家月份用电度数为度.
22.(1)解:设品牌电脑的单价是万元,则品牌电脑的单价是万元,根据题意得:,
化简得
解得:,(舍去),
经检验,是所列方程的解,且符合题意,
∴品牌电脑的单价是万元元,则品牌电脑的单价是万元即元.
答:品牌电脑的单价是元,品牌电脑的单价是元;
(2)解:设购买台品牌电脑,则购买台品牌电脑,
根据题意得:,
解得:.
设学校购买这些电脑需要元,则,
即,
,
随的增大而减小,
当时,取得最小值,最小值为(元).此时,
∴该公司费用最少的购买方案为购买台电脑,购买台电脑,最少需要元.
23.(1)解:设中级型汽车进货单价为元和紧凑型汽车进货单价为元,
由题意得,,
解得,
答:中级型汽车进货单价为元和紧凑型汽车进货单价为元.
(2)解:由题可得,,
,
,
随的增大而减小,
当时,有最大值为,
该经销商应购进中级型汽车辆,紧凑型汽车辆时,最大为万元.
24.(1)解:设每个甲种商品的进价为x元,
由题意可得:,
解得:,
经检验:是原方程的解,
∴每个甲、乙两种商品的进价分别是30元和40元;
(2)解:∵购进甲m个,则购进乙个,
则,
∴,
则,
∵,
∴当时,y最小,
即成本最少的方案为:购进甲种商品50个,乙种商品50个,最少成本为3500元.
25.(1)解:∵直线与轴交于点,与轴交于点,
当时,;
当时,
∴
∵直线交于点.
∴,
解得,
∴点;
(2)解:由题意得点P在直线上,设直线与直线交于点E,交x轴于点F,
将代入得,
∴,
①当点P在点E下方时,即,如图:
;
当点P在点E上方时,即,如图:
,
综上所述:的面积S与m的函数关系式为:;
(3)解:令直线为,直线为,
,则,
,
①如图1,若,,
过点Q作,
∴点G为中点,
∴,
则有,
,
或,
,或,
②如图2,图3,若或,
则,
,
或,
,或.
综上所述,M的坐标为或或或.
26.(1)解:根据图象可以得到:表示小聪的路程与时间的关系.
表示从学校到宁波天一阁,段表示查阅资料的时间,从第分钟,到分钟,则共用了分钟,
段表示从宁波天一阁到学校,时间是从第分钟到第分钟,共用了分钟,路程是千米,则速度是千米分钟,
(2)表示小明的路程与时间的关系,分钟走了千米,速度是千米分钟,则路程与时间的关系式是:
(3)设的函数关系式是,代入点
解得:
联立
解得:
当小聪与小明迎面相遇时,他们离学校的路程是千米.
27.(1)解:解方程组,得,
,
,
即.
设直线的解析式为,
则,解得,
直线的解析式为.
联立,解得,
点的坐标为.
(2)解:设点的坐标为,
,
,解得.
点在线段上,
,
.
设直线的解析式为,
把代入,
得,
解得,
直线的解析式为.
(3)解:存在.理由如下:
直线的解析式为,
记直线与轴交于点,
.
如图,当四边形为菱形时,,
,
有,
设点的坐标为,
有,
解得,
得点的坐标为;
当四边形为菱形时,,由,
同理可得点的坐标为;
易知直线与轴的交点的坐标为,
,
当四边形为菱形时,点的坐标为;
易知当以,,,为顶点的四边形是以为对角线的菱形时,
由菱形对角线互相垂直平分可得,
点与点关于对称,且,
,
点的坐标为.
综上所述,以,,,为顶点的四边形是菱形时,点的坐标为或或或.
答案第1页,共2页
答案第1页,共2页
